最近在看wenet项目时,发现其用的是相对位置编码。同时在做tts时,发现其效果还可以,但是就是对于长文本的生成效果不好,一直在思考是什么原因导致的,有想到最有可能是fastspeech是的绝对位置编码问题,所以还想着增大文本长度来重新训练,从实践角度来讲这是可以的,但是是治标不治本。直到最近研究了下相对位置编码,然后又翻vits的源码确认其也用的是相对位置编码,所以恍然大悟。这里总结下相对位置编码的原理,以做更深刻的理解。
一.动机
假设我们的文本为:“I think therefore I am”

如果我们要得到“I”的表示,第二个“I”的表示向量跟第一个“I”应该是不一样的,因为在第二个“I”时,有输入前面的“I think therefore”的隐藏状态信息,而第一个“I”只是输入一个初始化的隐藏状态信息。
如果不加入位置编码情况下(原始的transformer是不会在self-attention中加入位置编码的,只是在传入的时候加入绝对位置编码),那么transformer里面的self-attention会把两个位置上的“I”看做是同一个表示,从语义来看这是不合理的。

所以transformer的self-attention在不加入位置编码时,把两个位置的“I”看做一样来处理,这明显不合理,所以怎么来解决这个问题。如果加入绝对位置编码貌似可以解决问题,但是处理句子的能力只能是训练集中的最大长度,如果超过训练集中最大长度,模型就无能为力。
二.解决
了解到相对位置编码是从transformer-xl中了解到的,其实实际上是《Self-Attention with Relative Position Representations》这篇论文中首先提出来的。先来看下它引入的相对位置编码是怎样的?所谓的相对,从字面意思就是一个位置相对另一个位置。其采用一组可训练的embedding向量来表示输入句子中每个单词的位置编码。

如果我们以其中一个单词为中心,那么其有左边也有右边的单词,假设我们一个句子的长度为5,那么将有9个embedding向量可学习,一个embedding向量表示当前词,其中4个embedding向量用来表示其左边的单词,另外4个embedding向量来表示其左边的单词。为什么是9个embedding向量呢?因为我们在实际计算时候,5个单词都有可能作为中心词。上图中以第5个位置(索引为4)的单词为中心,那么其左边的单词的编号为:-1,-2,-3,-4,右边的单词的编号为:+1,+2,+3,+4 。
下面的图来表示这些embedding是怎么用的

对于第一个位置的单词“I”,当transformer计算“I”跟“therefore”的attention信息时候,"therefore"会采用第6个位置编码,因为我们是以第4个索引为中心,“therefore”是位于“I”的右边相对于“I”的相对距离为2,所以其采用的是第6个embedding向量。

跟之前一样,当计算到第二个“I”和其他单词的attention信息时,如计算其跟左边“therefore”的attention信息,那么“therefore”采用的位置编码为第3个embedding向量,因为它在“I”的左边相对于“I”偏离1个距离,索引应该采用第3个embedding向量。
三.RPR向量
先声明一些变量的,给出其作用先:
zi:输入单词i的输出表示
aij:单词i和单词j的权重系数
eij:单词i和单词j经过softmax后i对于j的关注程度
h:multihead attention的head个数
dx:输入序列的embedding size
dz:zi的embedding size

注意,有两个位置编码向量需要学习,一个是为了计算zi,一个是为了计算eij。最大的长度也会被考虑在内,如果我们中间索引为k,那么会有2k+1个相对位置编码向量需要学习,其中k个是其左边的,k个是其右边的,还有一个属于自己。如果长度超过2k+1,那么其右边超过k的全部置为k,左边超过k的全部置为0。下面是个长度为10的句子的例子,其中k=3,那么它到相对位置编码表中拿向量的索引为:

这么做的原因有:
1.作者认为超出范围的位置还采用精准的位置编码时没必要的
2.clip最大长度是的模型可以学到训练集中没见过的长度
四.实现
先看下传统的transformer没有采用RPR来计算zi向量的方式:
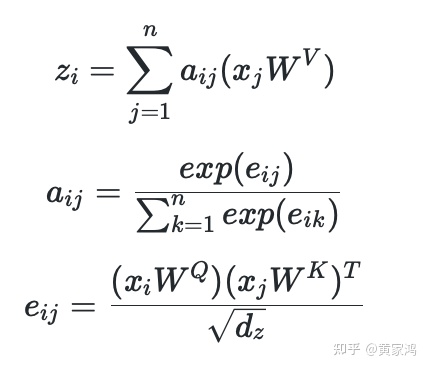
再看下采用RPR来计算的方式:
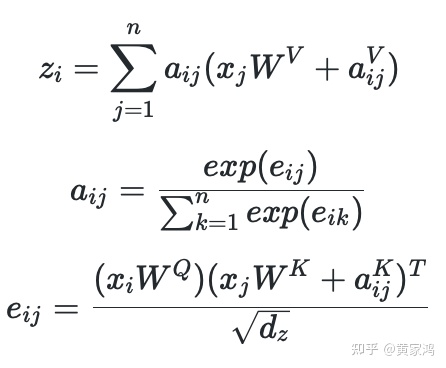
对比两种计算方式,比较容易看出来,其实是在计算zi的时候,计算完j跟权重w后加上i相对于j的相对位置编码。而在计算eij时候同理,计算完j跟权重w后加上ij的相对位置编码。注意这里两种权重矩阵是不同的,理解transformer中的q,k,v 这三个向量分别对应过去。
五.代码实现解析
实现代码参考:
https://github.com/tensorflow/tensor2tensor/blob/9e0a894034d8090892c238df1bd9bd3180c2b9a3/tensor2tensor/layers/common_attention.py#L1556-L1587
对于没有RPR的计算如下,是比较好计算的,代码通过矩阵的相乘直接可以得到eij.

如果要实现RPR,我们把其eij计算方式转换下得到:
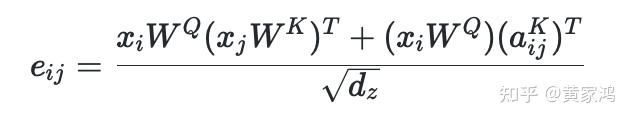
分子第一项中,我们的输入xi的tensor的Shape为:(B,h,seq_length,d),它计算的是query和key的关系,所以第一项的输出为(B,h,seq_length,seq_length)。了解transformer就知道其是多header,分子的第一项其实是比较好计算的,第二项的输出shape必须跟第一项一致。
第二项中,aijK表示的是ij的相对位置编码,从位置编码的Embeding向量table中去lookup得到的,位置编码的embedding向量table的Shape为(seq_length,seq_length,da),转换下维度得到(seq_length,da,seq_length),其中位置编码向量的table我们用A来表示,转换后得到AT。
xi跟WQ相乘后得到tensor其shape为(B,h,seq_length,dz),转换下维度得到(seq_length,B,h,dz),在转换下得到(seq_length,B*h,dz),再跟aijK来相乘,实质是跟AT相乘,所以(seq_length,B*h,dz)跟(seq_length,da,seq_length)矩阵相乘,dz=da,得到(seq_length,B*h,seq_length),reshape下得到(seq_length,B,h,seq_length),transpose为(B,h,seq_length,seq_length)这样就跟第一项对应起来了。
参考:
这篇文章基本上是算是参考第一个链接,只是没有完全按照它的翻译,而是用自己理解的话语写出来。
https://medium.com/@_init_/how-self-attention-with-relative-position-representations-works-28173b8c245amedium.com/@_init_/how-self-attention-with-relative-position-representations-works-28173b8c245a
Relative Multi-Headed Attentionnn.labml.ai/transformers/xl/relative_mha.html正在上传…重新上传取消
Attention Is All You Needarxiv.org/abs/1706.03762
编辑于 2022-09-24 17:19