一、基本思想
一般来说,只要问题可以划分成规模更小的子问题,并且原问题的最优解中包含了子问题的最优解,则可以考虑用动态规划解决。动态规划的实质是分治思想和解决冗余,因此,动态规划是一种将问题实例分解为更小的、相似的子问题,并存储子问题的解而避免计算重复的子问题,以解决最优化问题的算法策略。
由此可知,动态规划法与分治法和贪心法类似,它们都是将问题实例归纳为更小的、相似的子问题,并通过求解子问题产生一个全局最优解。
其中贪心法的当前选择可能要依赖已经作出的所有选择,但不依赖于有待于做出的选择和子问题。因此贪心法自顶向下,一步一步地作出贪心选择;
而分治法中的各个子问题是独立的 (即不包含公共的子子问题),因此一旦递归地求出各子问题的解后,便可自下而上地将子问题的解合并成问题的解。
但不足的是,如果当前选择可能要依赖子问题的解时,则难以通过局部的贪心策略达到全局最优解;如果各子问题是不独立的,则分治法要做许多不必要的工作,重复地解公共的子问题。解决上述问题的办法是利用动态规划。
该方法主要应用于最优化问题,这类问题会有多种可能的解,每个解都有一个值,而动态规划找出其中最优(最大或最小)值的解。若存在若干个取最优值的解的话,它只取其中的一个。在求解过程中,该方法也是通过求解局部子问题的解达到全局最优解,但与分治法和贪心法不同的是,动态规划允许这些子问题不独立,也允许其通过自身子问题的解作出选择,该方法对每一个子问题只解一次,并将结果保存起来,避免每次碰到时都要重复计算。因此,动态规划法所针对的问题有一个显著的特征,即它所对应的子问题树中的子问题呈现大量的重复。动态规划法的关键就在于,对于重复出现的子问题,只在第一次遇到时加以求解,并把答案保存起来,让以后再遇到时直接引用,不必重新求解。
递推过程:

二、习题
2.1斐波那契数列
斐波那契数列指的是这样一个数列 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233,377,610,987,1597,2584,4181,6765,10946,17711,28657
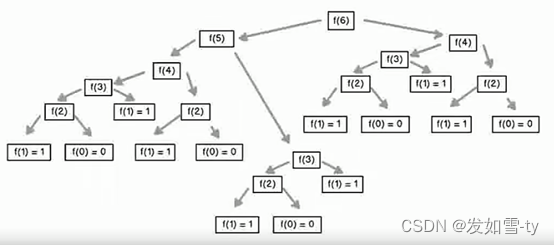
递归解法:
int Fib(int n)
{
if (n == 0)
return 0;
else if (n == 1)
return 1;
else
return Fib(n - 1) + Fib(n - 2);
}
递归+记忆法
vector<int> vc(20,-1);
int Fib2(int n)
{
if (n == 0)
return 0;
else if (n == 1)
return 1;
else
{
if (vc[n] != -1)
{
return vc[n];
}
else
{
int nret = Fib2(n - 1) + Fib2(n - 2);
int ntmp1;
int ntmp2;
if (vc[n-1] == -1)
{
ntmp1 = Fib2(n - 1);
vc[n - 1] = ntmp1;
}
else
{
ntmp1 = vc[n - 1];
}
if (vc[n - 2] == -1)
{
ntmp2 = Fib2(n - 2);
vc[n - 2] = ntmp1;
}
else
{
ntmp2 = vc[n - 2];
}
vc[n] = ntmp1 + ntmp2;
return vc[n];
}
}
}
void main()
{
int n = Fib1(6);
cout << n << endl;
n = Fib2(6);
cout << n << endl;
system("pause");
}
动态法:
int arry[100];
int Fib3(int n)
{
arry[0] = 0;
arry[1] = 1;
for (int i = 2; i <= n;i++)
{
arry[i] = arry[i - 1] + arry[i - 2];
}
return arry[n];
}
刚开始大家可以按照 递归==》递归+记忆化==》递推,后面熟悉了就可以直接递推。对于这个题目可以说是最简单的动态规划了。
2.2爬楼梯
一个人爬楼梯,每次只能爬1个或两个台阶,假设有n个台阶,那么这个人有多少种不同的爬楼梯方法。
分析:
如果n1,显然只有从0->1一种方法f(1)=1;
如果n2,那么有0->1->2、0->2两种方法f(2)=2;
如果n==3,那么可以先爬到第1阶,然后爬两个台阶,或者先爬到第二阶,然后爬一个台阶,显然f(3)=f(2)+f(1);
……
推广到一般情况,对于n(n>=3)个台阶,可以先爬到第n-1个台阶,然后再爬一个台阶,或者先爬到n-2个台阶,然后爬2个台阶,因此有f(n)=f(n-1)+f(n-2)。
那么动态规划的递推公式和边界条件都有了,即:
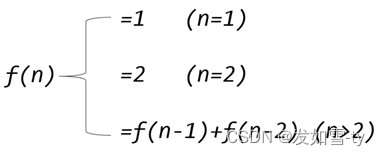
源码:
int dp(int stairs)
{
if (stairs == 1)
return 1;
int *dp = new int[stairs + 1];
dp[1] = 1;
dp[2] = 2;
for (int i = 3; i <= stairs; ++i)
{
dp[i] = dp[i - 2] + dp[i - 1];
}
int nret = dp[stairs];
delete[]dp;
return nret;
}
3.3 整数分割
给定一个正整数 n ,将其拆分为 k 个 正整数 的和( k >= 2 ),并使这些整数的乘积最大化。
返回 你可以获得的最大乘积 。
示例 1:
输入: n = 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1。
示例 2:
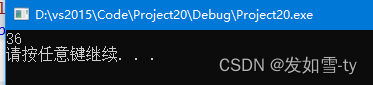
输入: n = 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。
说明: 你可以假设 n 不小于 2 且不大于 58。
#include<vector>
#include <algorithm>
using namespace std;
int max3(int a, int b, int c)
{
return max(a, max(b, c));
}
int integerBreak(int n) {
vector<int> dp(n + 1,-1);
for (int i = 2; i <= n; i++)//枚举需要拆分的数
{
dp[i] = i - 1;//初始化
for (int j = 1; j < i - 1; j++)//枚举并更新动态数组
{
dp[i] = max3(j * (i - j), j * dp[i - j], dp[i]);
}
}
return dp[n];
}
void main()
{
cout << integerBreak(10) << endl;
system("pause");
}
结果:
3.4 杨辉三角
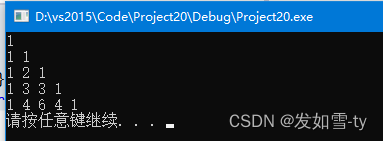
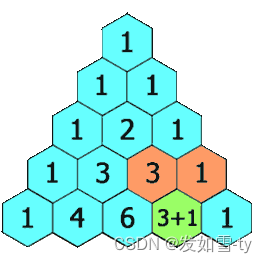
给定一个非负整数 numRows,生成「杨辉三角」的前 numRows 行。
在「杨辉三角」中,每个数是它左上方和右上方的数的和。
示例 1:
输入: numRows = 5
输出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]
示例 2:
输入: numRows = 1
输出: [[1]]
提示:
1 <= numRows <= 30
源码:
class Solution
{
public:
vector<vector<int>> generate(int numRows)
{
vector<vector<int>> ret(numRows);
for (int i = 0; i < numRows; ++i)
{
ret[i].resize(i + 1);
ret[i][0] = ret[i][i] = 1;
for (int j = 1; j < i; ++j)
{
ret[i][j] = ret[i - 1][j] + ret[i - 1][j - 1];
}
}
return ret;
}
};
void main()
{
Solution s;
auto vc = s.generate(5);
for (auto node :vc)
{
for (auto a:node)
{
cout << a << " ";
}
cout << endl;
}
system("pause");
}
结果: