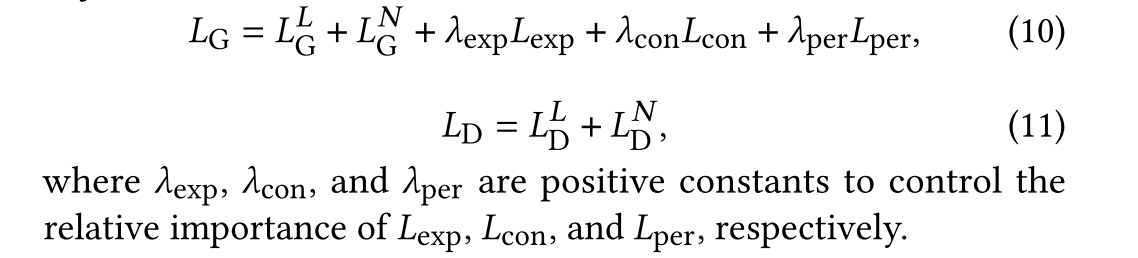1、线性回归基础概念：

• 回归模型：regression model
• 数据集：包含feature（输入变量）和与之对应的target（输出变量）
• 训练集：training set
• 输入数据：x（feature or input feature）
• 输出数据：y（“target”variable or output variable）
• （x,y）：signal training example
• m：number of training examples（训练集当中的训练数据有多少组m就是多少）
• （xⁱ,yⁱ）：i^th training example
• y-hat：y头顶一个^符号，表示y的估计值或预测值
  

---

2、cost function（代价函数）：

• 1、假设单变量线性回归，其模型可以看成：f=wx+b
• 2、其中w和b可以称为：parameter（参数）、coefficients（系数）、weight（权重）
• 3、对应的代价函数如下：注意代价函数除2是为了计算方便
  
• 4、当代价函数最小的时候，模型和数据的拟合度更高，所以我们的目的是让代价函数最小，下图是通过将模型f=wx+b中的b看成0，最终通过w获取最小代价函数的方法。
  
• 5、通过控制变量法（让b为0），研究w和代价函数之间的关系：
  
  • 可以看出有一个最适合的w对应最小的代价函数，但是从w开始不论增加还是减少，代价函数都会增大。
• 5、关于代价函数与w和b之间的关系：
  
• 通过等高线将3D关系转换为2D关系
  
• 通过（w,b）来对应出一个模型，可以看出改模型拟合程度较差：
  
• 2D的等高先当中椭圆的中心点就是对应代价函数最小的w和b，由此得到的模型拟合程度较高：
  

---

3、梯度下降算法

• 前言：
  • 在线性回归中，不必手动尝试w和b的最佳等高线图，我们可以用代码编写高效的算法自动查找可以使代价函数最小的w和b，从而获取和数据拟合度最高的模型。
  • 线性回归的代价函数J不一定都是上面介绍的那种方差形式，只不过上面那种形式是较为常见，且效果较好的函数。
• 梯度下降：gradient descent
• 梯度下降算法适合所有模型
• 从J（w,b）过渡到更一般使用的J（w1,w2,…wn,b）
• 对于J（w,b）模型的梯度下降算法而言：keep changing w,b to reduce J（w,b）,Until we settle at or near a minimum
• 梯度下降步骤：
  • 1、找到最陡的方向（环视一周）
  • 2、走一小步
  • 3、重复1步骤
  • 具体可参考下图：
    
• 梯度下降算法介绍：
  
  • 注意：其中α代表步长也可以叫学习率，后面的导数正负表示下将方向，导数的值也可以改变下降步长，具体可以参考下面两幅图：
    
    
  • 介绍梯度下降算法的推导过程，以及前面在代价函数中为什么要多除一个2
    
  • 梯度下降算法的伪代码表示
    

---

总结：上述内容，介绍了线性回归基础概念，又介绍了代价函数和梯度下降算法，线性回归是一种机器学习模型，而代价函数就是为了使模型更加准确而提出的一个评价依据，梯度下降算法就是获取最小代价函数的一种算法。

• 梯度下降算法执行过程：逐渐逼近或到达代价函数最小的位置
  
• 注意：在上述所讲的单变量线性回归模型中，每一次下降使用的是所有训练样本，所以这种梯度下降算法叫做”批量梯度下降“（Batch gradient descent）