矩阵快速幂和64位整数乘法
- 矩阵快速幂
- 64位整数乘法
矩阵快速幂
问题链接: AcWing 90. 64位整数乘法
问题描述:

分析
快速幂需要用到位运算的思想,求
a
b
a^b
ab,我们将
b
b
b转换成二进制的形式,假设
b
=
7
b=7
b=7,那么
a
7
=
a
(
111
)
2
=
a
2
0
+
2
1
+
2
2
=
a
∗
a
2
∗
a
4
a^7=a^{(111)_2}=a^{2^0+2^1+2^2}=a*a^2*a^4
a7=a(111)2=a20+21+22=a∗a2∗a4。
代码如下:
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
typedef long long ll;
ll ksm(ll a,ll b,ll p){
ll res=1;
while(b){
if(b&1) res=res*a%p;
b>>=1;
a=a*a%p;
}
return res%p;
}
int main(){
int n;
cin>>n;
while(n--){
int a,b,p;
scanf("%d%d%d",&a,&b,&p);
printf("%lld\n",ksm(a,b,p));
}
return 0;
}
64位整数乘法
问题链接: AcWing 90. 64位整数乘法
问题描述
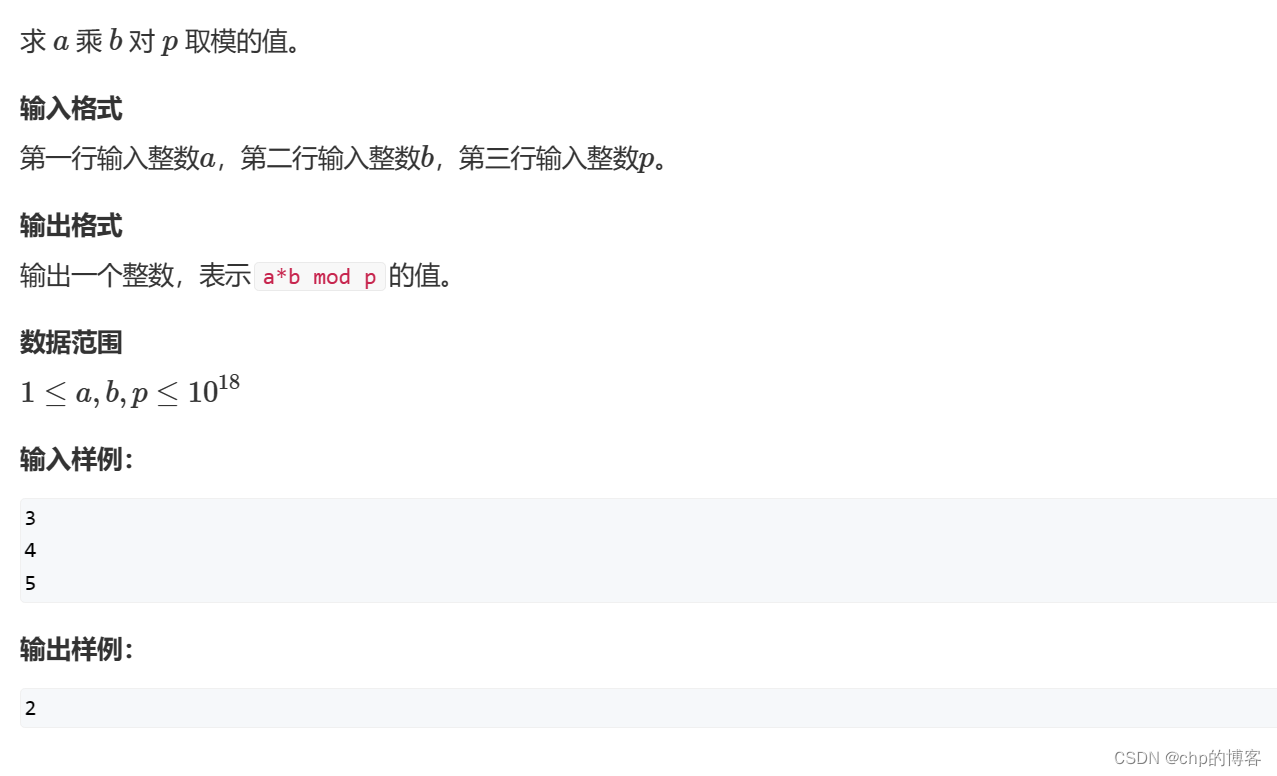
分析
大数乘法与快速幂的思想类似,都需要转化为位运算,
a
∗
b
a*b
a∗b假设
b
=
7
=
(
111
)
2
b=7=(111)_2
b=7=(111)2,
那么
a
∗
7
=
a
∗
(
111
)
2
=
a
∗
(
2
0
+
2
1
+
2
2
)
=
a
+
a
2
+
a
4
那么 a*7=a*{(111)_2}=a*(2^0+2^1+2^2)=a+a^2+a^4
那么a∗7=a∗(111)2=a∗(20+21+22)=a+a2+a4
代码如下:
#include<cstdio>
#include<algorithm>
#include<iostream>
#include<cstring>
using namespace std;
typedef long long ll;
ll ksm(ll a,ll b,ll p){
ll res=0;
while(b){
if(b&1) res=(res+a)%p;
a=2*a%p;
b>>=1;
}
return res%p;
}
int main(){
ll a,b,p;
cin>>a>>b>>p;
cout<<ksm(a,b,p);
return 0;
}