信号与系统复习笔记——通讯系统

复指数与正弦幅度调制

$$y(t)=x(t)c(t)$$

上式称为调制，其中 $x(t)$ 称为 调制信号 ，而 $c(t)$ 称为 载波信号 ， $y(t)$ 称为 已调信号 。 调制 的目的就是将低频信号搬运到高频信号中进行传输。

复指数载波的幅度调制

幅度调制通常有两种形式，一种是复指数的：

$$c(t)=e^{j({\omega }_{c}t+{\theta }_c)}$$

另一种是正弦的：

$$c(t)=\cos ({\omega }_{c}t+{\theta }_c)$$

在这两种情况下 ${\omega }_c$ 称为载波频率。先考虑复指数的情况，为了方便，我们令 ${\theta }_c=0$ ：

$$y(t)=x(t)e^{j{\omega }_{c}t}$$

$$Y(j\omega )=\frac{1}{2\pi }X(j\omega )\ast C(j\omega )$$

已知 $C(j\omega )=2\pi \delta (\omega -{\omega }_c)$ ，因此有：

$$Y(j\omega )=X(j(\omega -{\omega }_c))$$

由此可见， $Y(j\omega )$ 实际上就是将 $X(j\omega )$ 平移了 ${\omega }_c$ 。

将信号还原只需要乘以 $e^{-j{\omega }_{c}t}$ 即可，这个过程称为 解调 。

大多数情况下，传输的信号都是实信号，因为：

$$y(t)=x(t)\cos ({\omega }_{c}t)+jx(t)\sin ({\omega }_{c}t)$$

因此可以将调制系统表示为：

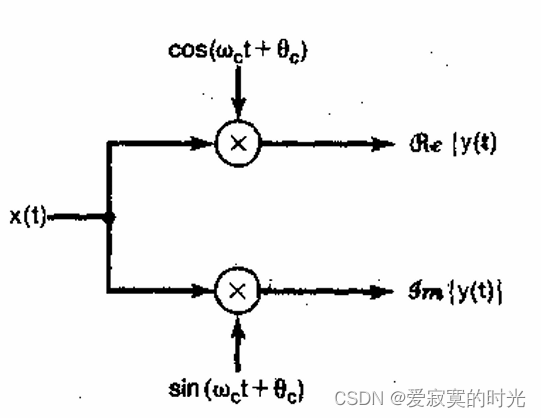
即实部和虚部分开传输。

正弦载波的幅度调制

正弦载波的载波函数为：

$$c(t)=\cos ({\omega }_{c}t+{\theta }_c)$$

相当于复指数载波只传输实部或者虚部，选 ${\theta }_c=0$ 此时载波信号的频谱为：

$$C(j\omega )=\pi [\delta (\omega -{\omega }_c)+\delta (\omega +{\omega }_c)]$$

频域卷积得到：

$$Y(j\omega )=\frac{1}{2}[X(j(\omega -{\omega }_c))+X(j(\omega +{\omega }_c))]$$

频谱的性质是各在频点 $\pm {\omega }_c$ 处有一个原信号频率的重复。结果只要 ${\omega }_M<{\omega }_c$ 就能从载波的信号中恢复出原始信号。

正弦幅度解调制

同步解调

将调制信号 $y(t)=x(t)\cos {\omega }_{c}t$ 再次乘以相同的载波函数，得到：

$$w(t)=y(t)\cos {\omega }_{c}t$$

相当于在0点处生成原始频率频谱。

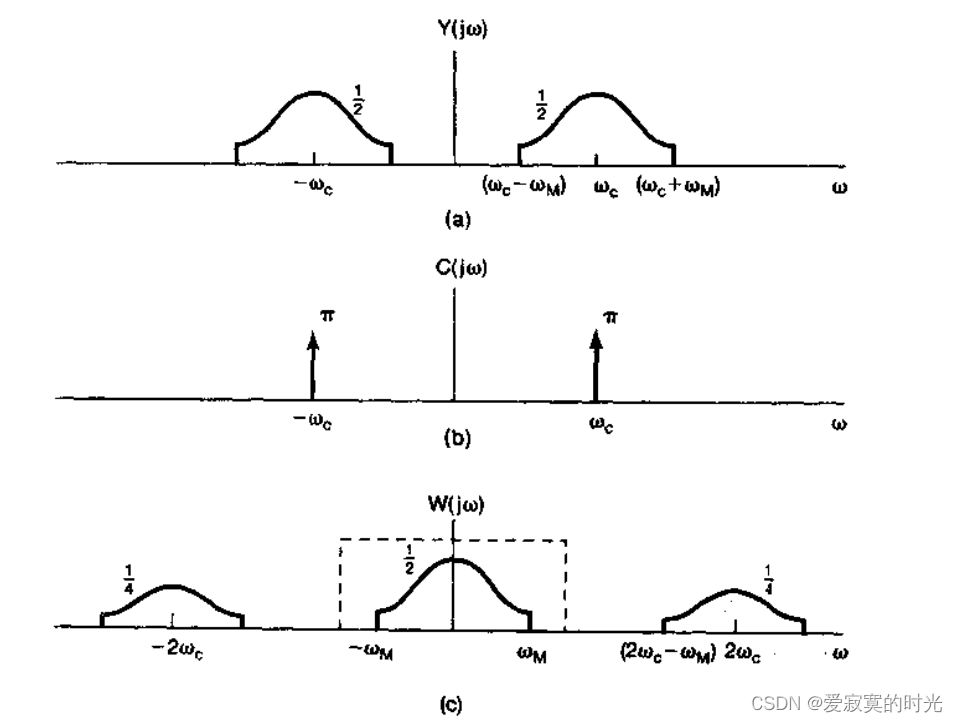
再通入一个截止频率为 ${\omega }_M$ ，增益为2的低通滤波器即可。

我们假设调制器和解调器的载波频率和相位都是相同的，这称为 同步解调 。同理，复指数的载波函数 $e^{j({\omega }_{c}t+{\theta }_c)}$ 的解调函数为 $e^{-j({\omega }_{c}t+{\theta }_c)}$ 。

当调制器和解调器相位不同的时候，假设调制相位为 ${\theta }_c$ 解调相位为 ${\varphi }_c$ 那么还原的信号为：

$$w(t)=e^{j({\theta }_c-{\varphi }_c)}x(t)$$

此时 $w(t)$ 相对于原信号有个复因子，可以恢复出原始信号。

而对于正弦调制信号来说：

$$w(t)=\frac{1}{2}\cos ({\theta }_c-{\varphi }_c)x(t)+\frac{1}{2}\cos (2{\omega }_{c}t+{\theta }_c+{\varphi }_c)x(t)$$

经过低通滤波之后的分量为 $\frac{1}{2}\cos ({\theta }_c-{\varphi }_c)x(t)$ ，可见有一个余弦因子。当同相位的时候，衰减最小，当正交相位的时候，衰减最大，输出为零。

非同步解调

非同步解调避免了同步调制需要同步相位和频率的困难，具体的，当 ${\omega }_c$ 远大于 ${\omega }_M$ 的时候，调制信号波形如图：

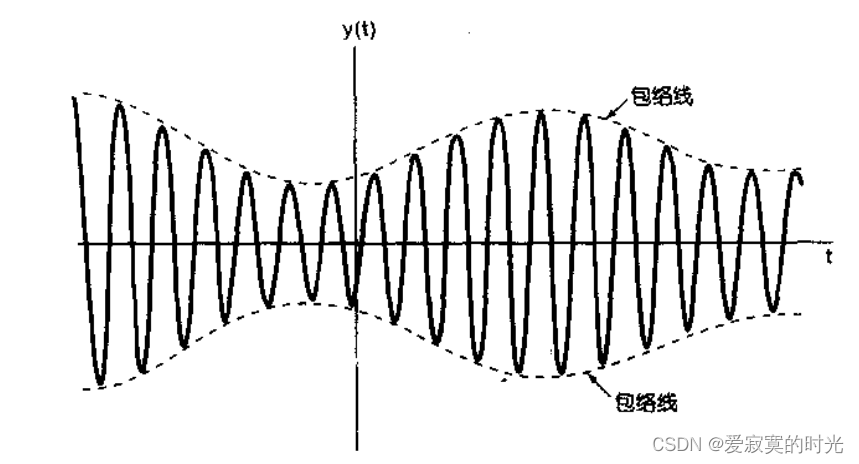
此时连接 $y(t)$ 峰值的曲线我们称为 包络线 ，是 $x(t)$ 的一种近似。通过提取这一个包络，可以近似的还原原始信号，这样的系统称为包络检波器，如图：

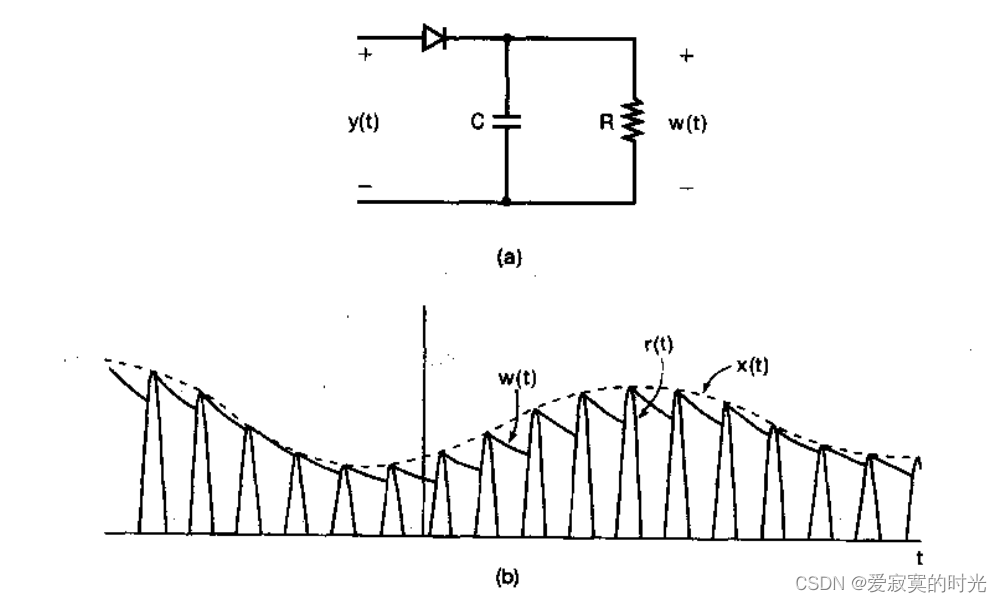
非同步解调需要满足两个条件：

1. $x(t)$ 总是正的。
2. ${\omega }_c$ 远大于 ${\omega }_M$ ，包络线易被还原。

通常我们可以将信号加上一个常数值 $A$ 保证总是正的，若 $|x(t)|\le K$ ，那么 $A>K$ ，这里 $K/A$ 称为调制指数 $m$ 。用百分数表示，称为调制百分数。

频分多路复用

当通信信道的带宽大于原始信号的带宽的时候，这时候可以将原来频率上互相重叠的原始信号通过不同的调制频率搬到不同的频带上，再次传输，称为频分多路复用。

单边带正弦幅度调制