文章目录
- 图论中的图属性
- 最短路径算法
- - Dijkstra算法
- 1. 算法介绍
- 2. 适用场景
- 3. 场景举例
- - Bellman-Ford算法
- 1. 算法介绍
- 2. 适用场景
- 3. 场景举例
- - Floyd-Warshall算法
- 1. 算法介绍
- 2. 适用场景
- 3. 场景举例
- 具体实现方案
- - JGraphT
- 小结
图论中的图属性
图论中,图的属性可以分为以下几个方面:
-
顶点:每个顶点(节点)可以具有自定义的属性,例如标签、值、坐标等。
-
边:每条边可以具有自定义的属性,例如权重(用于有权图)、方向(有向图)、容量(用于网络流图)等。
-
连通性:描述节点之间是否存在路径或连通的关系。如果图中的任意两个节点之间都存在路径,称为全连通图。如果只有部分节点之间存在路径,称为非连通图。
-
有权图:(Weighted Graph)是由一组顶点和一组边组成的图,每条边都有一个权重或者成本与之关联。这些权重可以表示两个顶点之间的距离、成本、容量等。在有权图中,每条边的权重可以为正数、零或负数。
-
无权图:(Unweighted Graph),又称为简单图或等权图,是由一组顶点和一组边组成的图,每条边都没有权重或者权重都相同。在无权图中,所有的边都被视为具有相等的权重或距离,所以边的权重通常被设定为1。
-
负权图:(Negative Weighted Graph)是有权图的一种特殊情况,其中至少存在一条边的权重为负数。在负权图中,路径的总权重可能为负数,这表示在此路径上从起点到终点的总消耗为负值。负权图在某些算法和问题中具有特殊的应用,例如最短路径算法中的"负权回路"问题。
-
有向图:(Directed Graph)表示图中的边具有方向性,即从一个节点指向另一个节点的关系。
-
无向图:(Undirected Graph)表示图中的边没有方向性,即节点之间的关系是双向的。
-
完全图:(Complete Graph)在一个无向图中,如果每对节点之间都有边连接,则称为完全图。在一个有向图中,如果每对节点之间都有方向相反的边连接,则称为强连通完全图。
最短路径算法
最短路径算法是图论中的经典问题,用于寻找两个节点之间的最短路径。下面是几种常见的最短路径算法。
- Dijkstra算法
1. 算法介绍
Dijkstra算法用于解决单源最短路径问题,即从一个固定节点出发,到其他节点的最短路径。它基于贪心策略,逐步扩展最短路径集合,直到到达目标节点或无法继续扩展为止。
它的核心思想是通过逐步扩展到达源节点的最短路径树,在每一步选择当前最短路径上的节点进行扩展,直到所有节点都被包含在最短路径树中。
2. 适用场景
Dijkstra算法适用于无权图或非负权图。常用于路网规划、地图导航、网络路由等场景。
3. 场景举例
在一个地理地图中,当计算两个城市之间的最短路径或者规划一条最短行车路线时,Dijkstra算法可以被应用。
- Bellman-Ford算法
1. 算法介绍
Bellman-Ford算法用于解决单源最短路径问题,与Dijkstra算法不同,它可以处理含有负权边的图。算法通通过迭代计算每个节点的最短路径估计值,并逐渐收敛到最优解,检测负权环以避免无限循环。
它的核心思想是利用松弛操作(即更新节点的最短路径估计值),通过迭代进行多轮松弛操作,直到不再存在可以改进的最短路径。
2. 适用场景
Bellman-Ford算法适用于带有负权边的图。常用于网络拓扑计算、检测负权环等场景。
3. 场景举例
在一个计费系统中,当计算从一个节点到其他节点的最低费用时,Bellman-Ford算法可以被应用。
- Floyd-Warshall算法
1. 算法介绍
Floyd-Warshall算法用于解决全源最短路径问题,即求解任意两个节点之间的最短路径。该算法利用动态规划的思想,通过中转节点不断优化路径的长度,最终得到所有节点对之间的最短路径。
它的核心思想是通过中间节点的枚举来逐步逼近最短路径。算法创建一个二维矩阵来存储任意两个节点之间的最短路径长度,通过不断更新矩阵中的值来得到最终的最短路径。Floyd算法的时间复杂度为O(n^3),适用于节点数量不是很大的情况。
2. 适用场景
Floyd-Warshall算法适用于小规模图,可以求解所有节点对之间的最短路径。常用于交通网络路由、图数据库中的查询优化等场景。
3. 场景举例
在一个城市交通系统中,当计算任意两个交通站点之间的最短路径或者最佳路线时,Floyd-Warshall算法可以被应用。
具体实现方案
- JGraphT
JGraphT是一个用于图算法的Java库,它提供了许多常见的图算法实现,包括Dijkstra算法。Dijkstra算法用于找到带权图中从一个顶点到其他顶点的最短路径。
maven配置:
<dependency>
<groupId>org.jgrapht</groupId>
<artifactId>jgrapht-core</artifactId>
<version>1.4.0</version>
</dependency>
路径图如下:
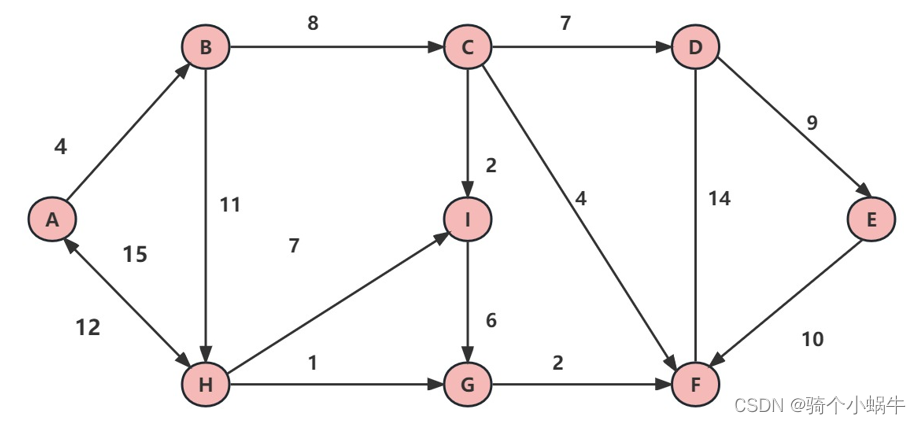
源码:
/**
* 最短路径
* @param vertexs 顶点集合
* @param edgeWeights 边权重集合
* @param srcVertexs 源顶点集合
* @param dstVertexs 目的顶点集合
*/
public static List<ShortestPathInfo> shortestPath(List<String> vertexs, List<EdgeWeight> edgeWeights, List<String> srcVertexs, List<String> dstVertexs) {
log.info("====================================== shortestPath start ======================================");
StopWatch stopWatch = new StopWatch();
// 创建有向加权图
stopWatch.start("创建有向加权图");
Graph<String, DefaultWeightedEdge> graph = new DefaultDirectedWeightedGraph<>(DefaultWeightedEdge.class);
stopWatch.stop();
log.info("{}耗时:{}毫秒", stopWatch.getLastTaskName(), stopWatch.getLastTaskTimeMillis());
// 添加顶点
stopWatch.start("添加顶点");
for (String vertex : vertexs) {
graph.addVertex(vertex);
}
stopWatch.stop();
log.info("{}耗时:{}毫秒", stopWatch.getLastTaskName(), stopWatch.getLastTaskTimeMillis());
// 添加边权重
stopWatch.start("添加边权重");
for (EdgeWeight edgeWeight : edgeWeights) {
graph.addEdge(edgeWeight.getStartPoint(), edgeWeight.getEndPoint());
graph.setEdgeWeight(edgeWeight.getStartPoint(), edgeWeight.getEndPoint(), edgeWeight.getWeight());
}
stopWatch.stop();
log.info("{}耗时:{}毫秒", stopWatch.getLastTaskName(), stopWatch.getLastTaskTimeMillis());
// 创建最短路径算法对象
stopWatch.start("创建最短路径算法对象");
DijkstraShortestPath<String, DefaultWeightedEdge> algorithm = new DijkstraShortestPath<>(graph);// - 创建DijkstraShortestPath对象
// BellmanFordShortestPath<String, DefaultWeightedEdge> algorithm = new BellmanFordShortestPath<>(graph);// - 创建BellmanFordShortestPath对象
// FloydWarshallShortestPaths<String, DefaultWeightedEdge> algorithm = new FloydWarshallShortestPaths<>(graph);// - 创建FloydWarshallShortestPaths对象
stopWatch.stop();
log.info("{}耗时:{}毫秒", stopWatch.getLastTaskName(), stopWatch.getLastTaskTimeMillis());
// 原顶点集合和目标顶点集合
stopWatch.start("原顶点集合和目标顶点集合");
if (ObjectUtils.isEmpty(srcVertexs)) {
srcVertexs = new ArrayList<>(graph.vertexSet());// 全部顶点
}
if (ObjectUtils.isEmpty(srcVertexs)) {
dstVertexs = new ArrayList<>(graph.vertexSet());// 全部顶点
}
stopWatch.stop();
log.info("{}耗时:{}毫秒", stopWatch.getLastTaskName(), stopWatch.getLastTaskTimeMillis());
// 计算最短路径
stopWatch.start("计算最短路径");
List<ShortestPathInfo> list = new ArrayList<>();
for (String src : srcVertexs) {
for (String dst : dstVertexs) {
if (!src.equals(dst)) {
GraphPath<String, DefaultWeightedEdge> path1 = algorithm.getPath(src, dst);
double pathWeight = algorithm.getPathWeight(src, dst);
ShortestPathInfo shortestPathInfo = new ShortestPathInfo(src, dst, path1 != null ? path1.getVertexList() : new ArrayList<>(), pathWeight);
list.add(shortestPathInfo);
}
}
}
stopWatch.stop();
log.info("{}耗时:{}毫秒", stopWatch.getLastTaskName(), stopWatch.getLastTaskTimeMillis());
log.info("总耗时:{}毫秒", stopWatch.getTotalTimeMillis());
log.info("====================================== shortestPath end ======================================");
return list;
}
public static void main(String[] args) {
List<String> vertexs = Stream.of("A","B","C","D","E","F","G","H","I").collect(Collectors.toList());
List<String> edgeWeightsList = new ArrayList<>();
edgeWeightsList.add("A,B,4");
edgeWeightsList.add("A,H,15");
edgeWeightsList.add("H,A,12");
edgeWeightsList.add("B,H,11");
edgeWeightsList.add("H,I,7");
edgeWeightsList.add("B,C,8");
edgeWeightsList.add("H,G,1");
edgeWeightsList.add("C,I,2");
edgeWeightsList.add("I,G,6");
edgeWeightsList.add("C,D,7");
edgeWeightsList.add("C,F,4");
edgeWeightsList.add("D,F,14");
edgeWeightsList.add("D,E,9");
edgeWeightsList.add("E,F,10");
edgeWeightsList.add("G,F,2");
List<EdgeWeight> edgeWeights = new ArrayList<>();
for (String s : edgeWeightsList) {
String[] split = s.split(",");
edgeWeights.add(new EdgeWeight(split[0], split[1], Double.valueOf(split[2])));
}
List<String> srcVertexs = Stream.of("A","B","C").collect(Collectors.toList());
List<String> dstVertexs = Stream.of("F","G","I").collect(Collectors.toList());
List<ShortestPathInfo> list = ShortestPathUtil.shortestPath(vertexs, edgeWeights, srcVertexs, dstVertexs);
list.stream().forEach(sp -> log.info("=====顶点{}-顶点{}=====最短路径:{}=====权重:{}", sp.getSrcVertex(), sp.getDstVertex(), sp.getPath().toString(), sp.getWeight()));
}
}
输出:
00:08:51.208 [main] INFO com.joker.util.ShortestPathUtil - ====================================== shortestPath start ======================================
00:08:51.240 [main] INFO com.joker.util.ShortestPathUtil - 创建有向加权图耗时:26毫秒
00:08:51.245 [main] INFO com.joker.util.ShortestPathUtil - 添加顶点耗时:3毫秒
00:08:51.246 [main] INFO com.joker.util.ShortestPathUtil - 添加边权重耗时:1毫秒
00:08:51.256 [main] INFO com.joker.util.ShortestPathUtil - 创建最短路径算法对象耗时:9毫秒
00:08:51.260 [main] INFO com.joker.util.ShortestPathUtil - 原顶点集合和目标顶点集合耗时:4毫秒
00:08:51.278 [main] INFO com.joker.util.ShortestPathUtil - 计算最短路径耗时:17毫秒
00:08:51.278 [main] INFO com.joker.util.ShortestPathUtil - 总耗时:62毫秒
00:08:51.278 [main] INFO com.joker.util.ShortestPathUtil - ====================================== shortestPath end ======================================
00:08:51.279 [main] INFO com.joker.util.ShortestPathUtil - =====顶点A-顶点F=====最短路径:[A, B, C, F]=====权重:16.0
00:08:51.280 [main] INFO com.joker.util.ShortestPathUtil - =====顶点A-顶点G=====最短路径:[A, H, G]=====权重:16.0
00:08:51.280 [main] INFO com.joker.util.ShortestPathUtil - =====顶点A-顶点I=====最短路径:[A, B, C, I]=====权重:14.0
00:08:51.280 [main] INFO com.joker.util.ShortestPathUtil - =====顶点B-顶点F=====最短路径:[B, C, F]=====权重:12.0
00:08:51.280 [main] INFO com.joker.util.ShortestPathUtil - =====顶点B-顶点G=====最短路径:[B, H, G]=====权重:12.0
00:08:51.280 [main] INFO com.joker.util.ShortestPathUtil - =====顶点B-顶点I=====最短路径:[B, C, I]=====权重:10.0
00:08:51.280 [main] INFO com.joker.util.ShortestPathUtil - =====顶点C-顶点F=====最短路径:[C, F]=====权重:4.0
00:08:51.281 [main] INFO com.joker.util.ShortestPathUtil - =====顶点C-顶点G=====最短路径:[C, I, G]=====权重:8.0
00:08:51.281 [main] INFO com.joker.util.ShortestPathUtil - =====顶点C-顶点I=====最短路径:[C, I]=====权重:2.0
小结
这些最短路径算法各自有不同的适用场景和复杂度。选择合适的算法取决于图的特点(有向或无向、权重正负等)和问题的具体需求(单源或全源最短路径)。