并查集基础
并查集(Union-find Sets)是一种非常精巧而实用的数据结构,它主要用于处理一些不相交集合的合并问题。一些常见的用途有求
连通子图、求最小生成树的Kruskal算法和求最近公共祖先(LCA)等。
并查集的基本操作主要有:
- 初始化
init- 查询
find- 合并
unionn
//1. 初始化 init
void init(int n)
{
for(int i = 1; i <= n; i++)
fa[i] = i; //将每个结点的祖先初始为自己
}
//2. 查询 find
int find(int i)
{
if(i == fa[i])//找到祖先
return i;
else{
fa[i] = find(fa[i]); //该步使用递归进行路径压缩
return fa[i]; //返回父节点
}
}
//3. 合并 unionn
void unionn(int i, int j)
{
int i_fa = find(i); //找到 i 的祖先
int j_fa = find(j); //找到 j 的祖先
fa[i_fa] = j_fa; // i的祖先指向j的祖先
}
❓ 685. 冗余连接 II
难度:困难
在本问题中,有根树指满足以下条件的 有向 图。该树只有一个根节点,所有其他节点都是该根节点的后继。该树除了根节点之外的每一个节点都有且只有一个父节点,而根节点没有父节点。
输入一个有向图,该图由一个有着 n 个节点(节点值不重复,从 1 到 n)的树及一条附加的有向边构成。附加的边包含在 1 到 n 中的两个不同顶点间,这条附加的边不属于树中已存在的边。
结果图是一个以边组成的二维数组 edges 。 每个元素是一对 [ui, vi],用以表示 有向 图中连接顶点 ui 和顶点 vi 的边,其中 ui 是 vi 的一个父节点。
返回一条能删除的边,使得剩下的图是有 n 个节点的有根树。若有多个答案,返回最后出现在给定二维数组的答案。
示例 1:

输入:edges = [[1,2],[1,3],[2,3]]
输出:[2,3]
示例 2:
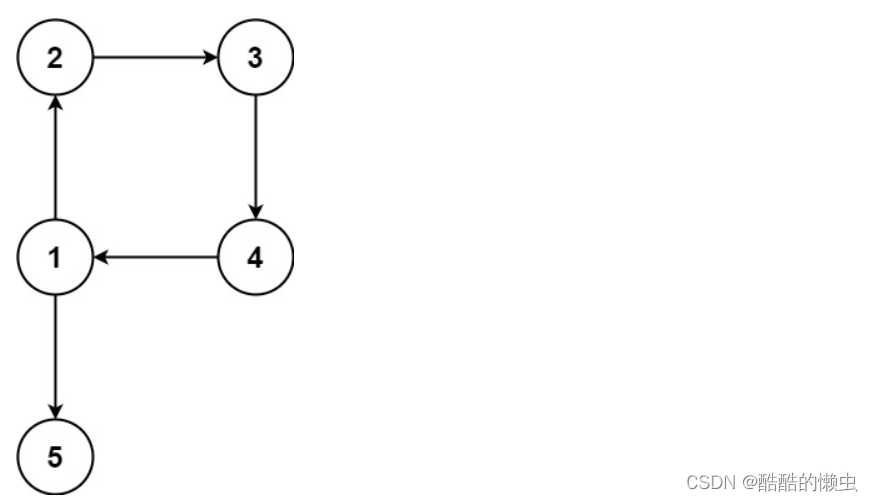
输入:edges = [[1,2],[2,3],[3,4],[4,1],[1,5]]
输出:[4,1]
提示:
- n = = e d g e s . l e n g t h n == edges.length n==edges.length
- 3 < = n < = 1000 3 <= n <= 1000 3<=n<=1000
- e d g e s [ i ] . l e n g t h = = 2 edges[i].length == 2 edges[i].length==2
- 1 < = u i , v i < = n 1 <= ui, vi <= n 1<=ui,vi<=n
💡思路:(并查集)
由树的定义得,除根节点,剩余结点的入度都为
1
在不增加节点的情况下多加了一条边,增加后有两种情况:
- 所有结点(包含根节点)的入度都为
1,则新增的这条边指向了根节点,存在有向环;- 删除组成环最后一条边即可。
- 其中包含了一个入度 为
2的结点,则这条边指向了该节点;假如两条边先后出现的顺序是[a,c]和[b,c]:在边集中去掉[b,c],判断剩下的边集中是否存在圈:- 如果存在圈,则删掉
[a,c]。 - 不存在圈,则删掉
[b,c].
- 如果存在圈,则删掉
🍁代码:(C++、Java)
C++
class Solution {
private:
static const int N = 1001; //所给数组edges的大小在3到1000范围内
int father[N];
int n; //边的的数量
//并查集初始化
void init(){
for(int i = 1; i <= n; i++)
father[i] = i;
}
//并查集寻根
int find(int u){
return u == father[u] ? u : father[u] = find(father[u]);
}
//并查集合并,将v->u这条边加入并查集
void unionn(int v, int u){
v = find(v);
u = find(u);
if(u == v) return;
father[u] = v;
}
//判断u 和 v 是否找到同一个根
bool same(int v, int u){
return find(v) == find(u);
}
// 在有向图里找到删除的那条边,使其变成树
vector<int> getRemoveEdge(const vector<vector<int>>& edges){
init(); //初始化并查集
for(int i = 0; i < n; i++){//遍历所有的边
if(same(edges[i][0], edges[i][1])){ //构成有向环,找到了要删除的边
return edges[i];
}
unionn(edges[i][0], edges[i][1]);
}
return {};
}
//删一条边之后判断是不是树
bool isTree(const vector<vector<int>>& edges, int deleteEdge){
init(); //初始化并查集
for(int i = 0; i < n; i++){
if(i == deleteEdge) continue; // 删除第deleteEdge条边
if(same(edges[i][0], edges[i][1])){ // 构成了有向环,一定不是树
return false;
}
unionn(edges[i][0], edges[i][1]);
}
return true;
}
public:
vector<int> findRedundantDirectedConnection(vector<vector<int>>& edges) {
int inDegree[N] = {0}; // 记录每个结点的入度
n = edges.size(); //边的数量
for(int i = 0; i < n; i++){
inDegree[edges[i][1]]++; //统计入度
}
vector<int> tmp; // 记录入读为2的边,(如果有的话就只有两条)
//找入度为2的结点所对应的边,倒序插入
for(int i = n - 1; i >= 0; i--){
if(inDegree[edges[i][1]] == 2){
tmp.push_back(i);
}
}
//如果有入度为2,那么一定是两条边里删一个,看删哪一个可以构成树
if(tmp.size() > 0){
if(isTree(edges, tmp[0])){
return edges[tmp[0]];
}else{
return edges[tmp[1]];
}
}
//没有入度为 2 的结点,则一定存在有向环
return getRemoveEdge(edges);
}
};
Java
class Solution {
private static final int N = 1001; //所给数组edges的大小在3到1000范围内
private int[] father;
public Solution() {
father = new int[N];
// 并查集初始化
for (int i = 0; i < N; ++i) {
father[i] = i;
}
}
// 并查集里寻根
private int find(int u) {
if(u == father[u]) {
return u;
}
father[u] = find(father[u]);
return father[u];
}
// 并查集合并,将v->u这条边加入并查集
private void unionn(int v, int u) {
u = find(u);
v = find(v);
if (u == v) return ;
father[u] = v;
}
// 判断u 和 v 是否找到同一个根
private Boolean same(int u, int v) {
u = find(u);
v = find(v);
return u == v;
}
/**
* 初始化并查集
*/
private void initFather() {
// 并查集初始化
for (int i = 0; i < N; ++i) {
father[i] = i;
}
}
/**
* 在有向图里找到删除的那条边,使其变成树
* @param edges
* @return 要删除的边
*/
private int[] getRemoveEdge(int[][] edges) {
initFather();
for(int i = 0; i < edges.length; i++) {
if(same(edges[i][0], edges[i][1])) { // 构成有向环了,就是要删除的边
return edges[i];
}
unionn(edges[i][0], edges[i][1]);
}
return null;
}
/**
* 删一条边之后判断是不是树
* @param edges
* @param deleteEdge 要删除的边
* @return true: 是树, false: 不是树
*/
private Boolean isTreeAfterRemoveEdge(int[][] edges, int deleteEdge)
{
initFather();
for(int i = 0; i < edges.length; i++)
{
if(i == deleteEdge) continue;
if(same(edges[i][0], edges[i][1])) { // 构成有向环了,一定不是树
return false;
}
unionn(edges[i][0], edges[i][1]);
}
return true;
}
public int[] findRedundantDirectedConnection(int[][] edges) {
int[] inDegree = new int[N];
for(int i = 0; i < edges.length; i++)
{
// 入度
inDegree[ edges[i][1] ] += 1;
}
// 找入度为2的节点所对应的边,注意要倒序,因为优先返回最后出现在二维数组中的答案
ArrayList<Integer> twoDegree = new ArrayList<Integer>();
for(int i = edges.length - 1; i >= 0; i--)
{
if(inDegree[edges[i][1]] == 2) {
twoDegree.add(i);
}
}
// 处理图中情况1 和 情况2
// 如果有入度为2的节点,那么一定是两条边里删一个,看删哪个可以构成树
if(!twoDegree.isEmpty())
{
if(isTreeAfterRemoveEdge(edges, twoDegree.get(0))) {
return edges[ twoDegree.get(0)];
}
return edges[ twoDegree.get(1)];
}
// 明确没有入度为2的情况,那么一定有有向环,找到构成环的边返回就可以了
return getRemoveEdge(edges);
}
}
🚀 运行结果:
🕔 复杂度分析:
- 时间复杂度:
O
(
n
l
o
g
n
)
O(nlogn)
O(nlogn),其中
n是图中的节点个数。需要遍历图中的n条边,对于每条边,需要对两个节点查找祖先,如果两个节点的祖先不同则需要进行合并,需要进行 2 次查找和最多 1 次合并。一共需要进行2n次查找和最多n次合并,因此总时间复杂度是 O ( 2 n l o g n ) = O ( n l o g n ) O(2nlogn)=O(nlogn) O(2nlogn)=O(nlogn)。这里的并查集使用了路径压缩,但是没有使用按秩合并,最坏情况下的时间复杂度是 O ( n l o g n ) O(nlogn) O(nlogn),平均情况下的时间复杂度依然是 O ( n α ( n ) ) O(nα(n)) O(nα(n)),其中 α α α 为阿克曼函数的反函数, α ( n ) α(n) α(n) 可以认为是一个很小的常数。 - 空间复杂度: O ( N ) O(N) O(N),N = 1001。
题目来源:力扣。
放弃一件事很容易,每天能坚持一件事一定很酷,一起每日一题吧!
关注我LeetCode主页 / CSDN—力扣专栏,每日更新!