在做APP设计的时候,难免会遇到一些需要展示数据的场景。使用传统的表格和文档展示数据不仅难看,也影响用户理解数据的含义。而数据可视化设计能将数据以更加直观的方式展现出来,使数据更加客观、更有说服力。
在移动应用中,数据可视化设计尤为重要,它可以提高用户对数据的理解和感知,进而提升用户体验和用户满意度。因此在数据展示方面必须简单、直观。
数据可视化在移动端的主要体现是“数据图表”,它能将大量的数据进行快速、清晰的展示。我们最常用的数据设计组件就是:柱状图、折线图、环形图、散点图、饼图等,设计师可以根据用户需求、数据类型和分析目的选择合适的图表类型。
接下来我们一一介绍各个数据图表
1、柱状图
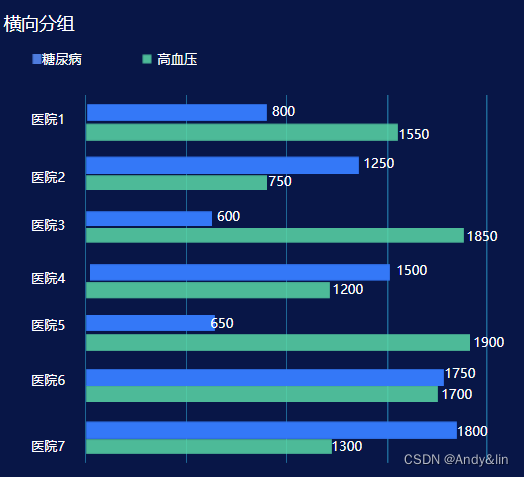
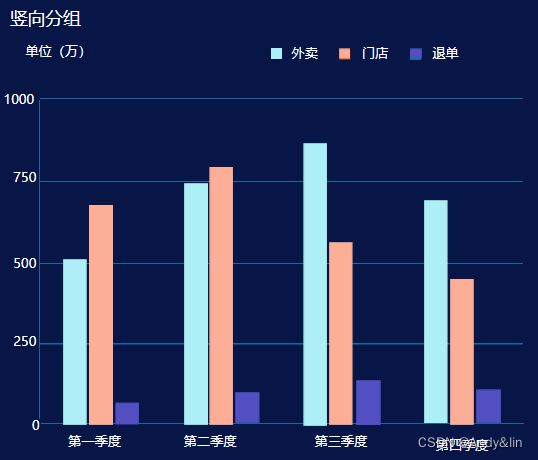
柱形图,又称长条图、柱状统计图、条图、条状图、棒形图,是一种以长方形的长度为变量的统计图表,用于对不同类型的数据进行数值比较,柱状图之间的条目相对独立,数据之间不需要有逻辑的关联性。我们常用的柱状图分为横向柱状图和纵向柱状图


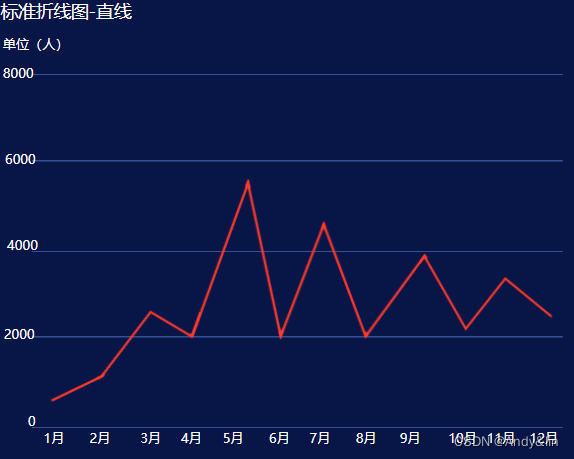
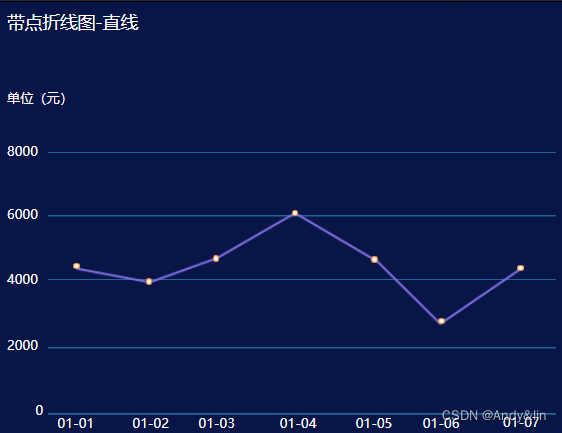
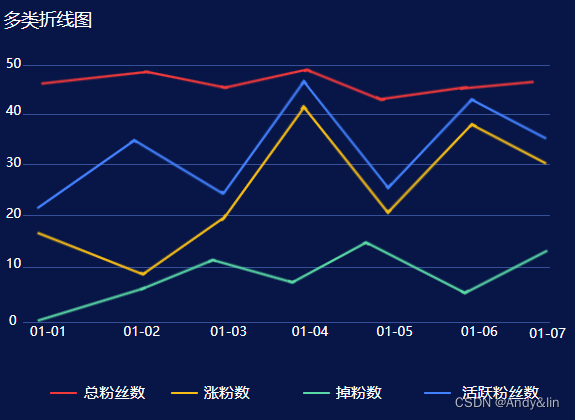
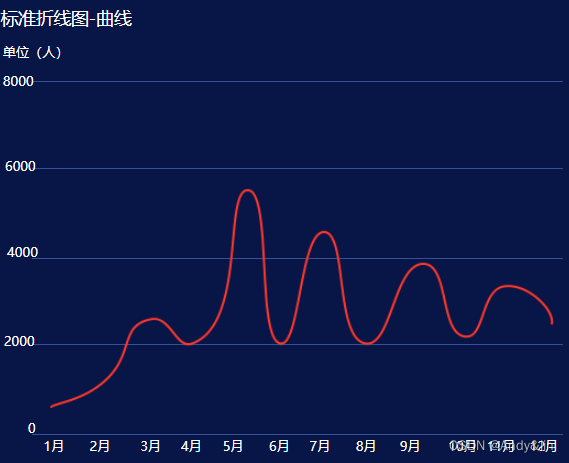
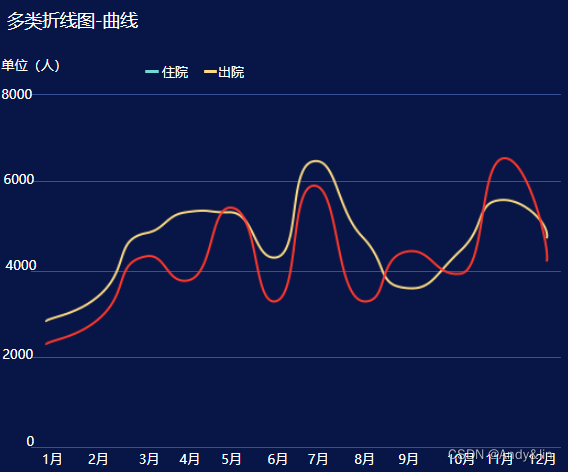
2、折线图
折线图通过线链接横向相邻数据的数据表现形式,通常相邻数据之间都有一定的逻辑关系,一般以时间属性为主,表达一定周期之内的趋势走向。
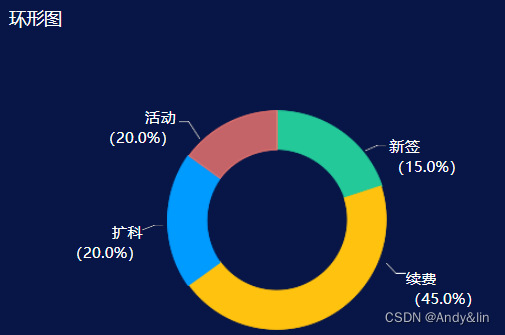
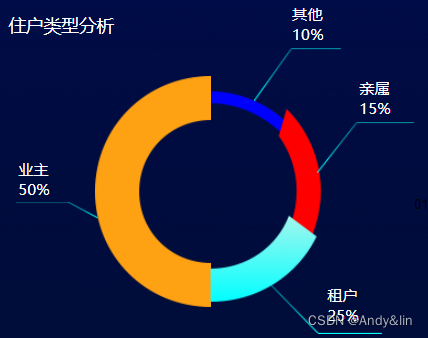
3、环形图
环形图是由两个及两个以上大小不一的饼图叠在一起,挖去中间的部分所构成的图形
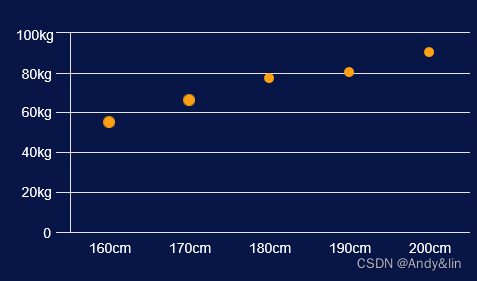
4、散点图
散点图是用两组数据数据构成多个坐标点,考察坐标点的分布,判断两变量之间是否存在关联或总结坐标点的分布模式
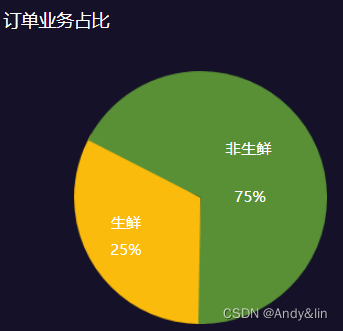
5、饼图
饼状图是一个划分为几个扇形的圆形统计图表,用于描述量、频率或百分比之间的相对关系

完成的移动端可视化设计,参考https://download.csdn.net/download/weixin_43516258/87982554

![python+requests库使用时报错:ssl.SSLError: [SSL: WRONG_VERSION_NUMBER] wrong version number (_ssl.c:1131)](https://img-blog.csdnimg.cn/img_convert/c5505c962594e410506cfafdc5ba0077.png)