突然变化的图像或信号
小波变换
高带宽?
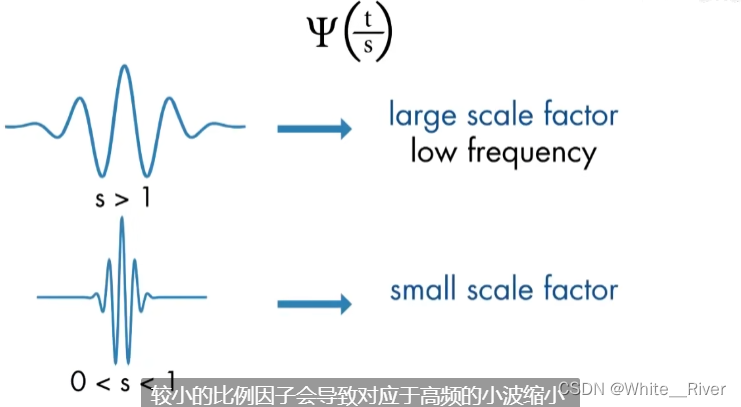
放缩和时延

放缩因子和频率成正比

小波在频域中具有带通特性
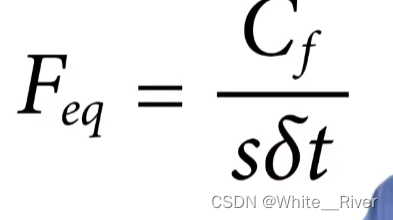
Cf 中心频率
s 小波刻度
\delta t 采样间隔
时延
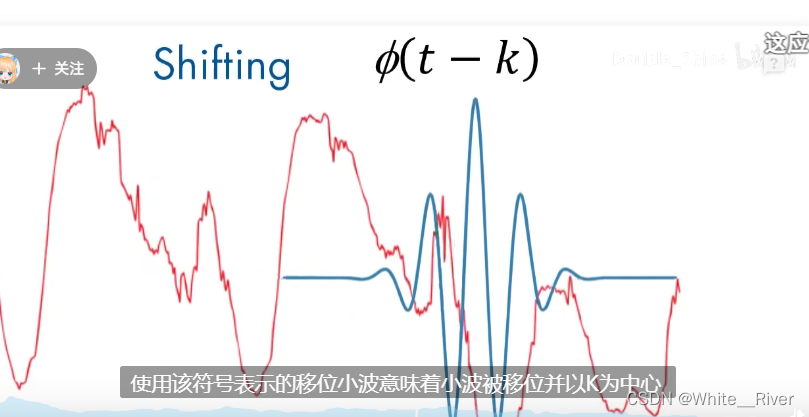
我们需要移动小波,以便使其和信号中寻找的特征对齐


- 时频分析
- 时域频率成分滤波

连续小波变换 CWT
利用此变换 可以获得信号的同时时频分析
simultaneous time frequency analysis


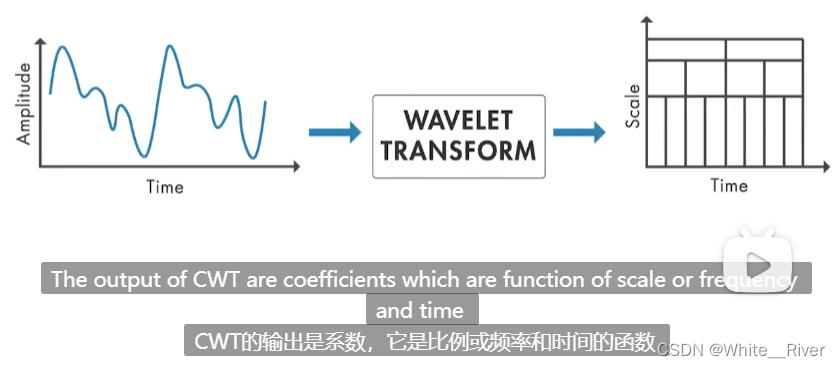
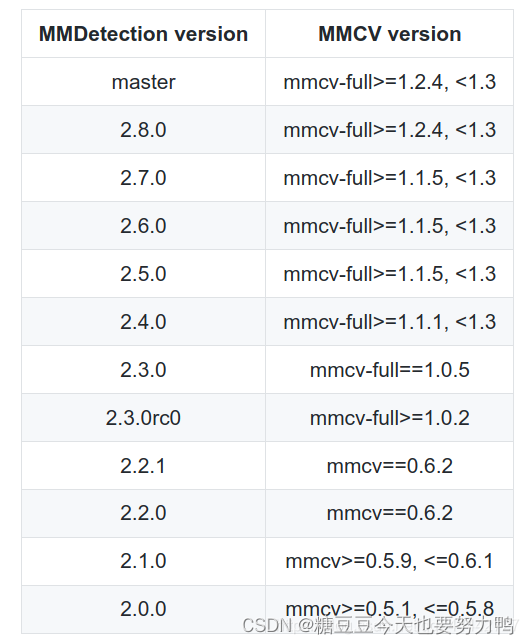
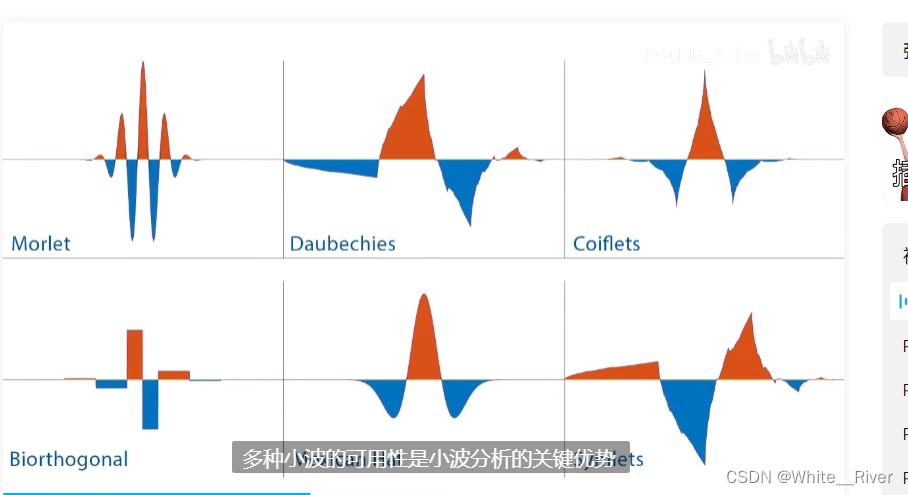
如何构造不同小波尺度
construct different wavelet scales

DWT

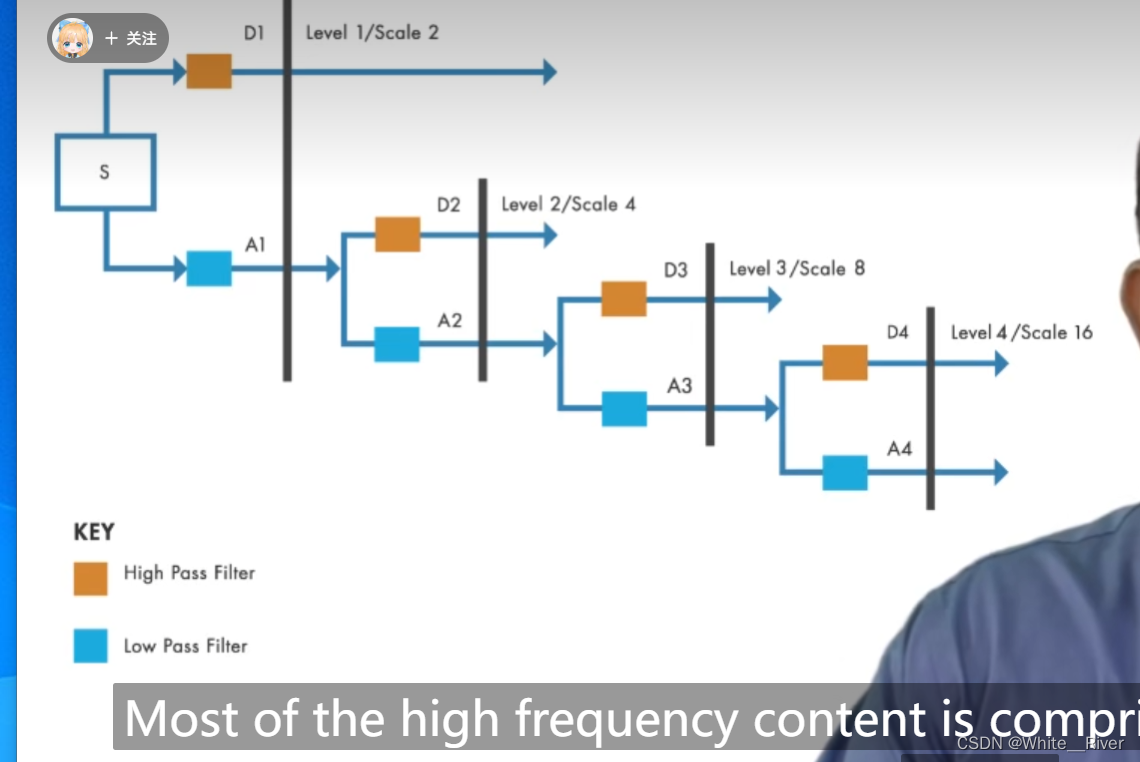
离散小波变换将信号变成低通子带(蓝色)和高通子带(黄色)
低通子带被称为近似等级 approximation level
高通子带被称为细节等级 detail level

离散小波变换去噪的过程
消除噪音的同时保持原信号有效的高频成分(急剧变化的成分)
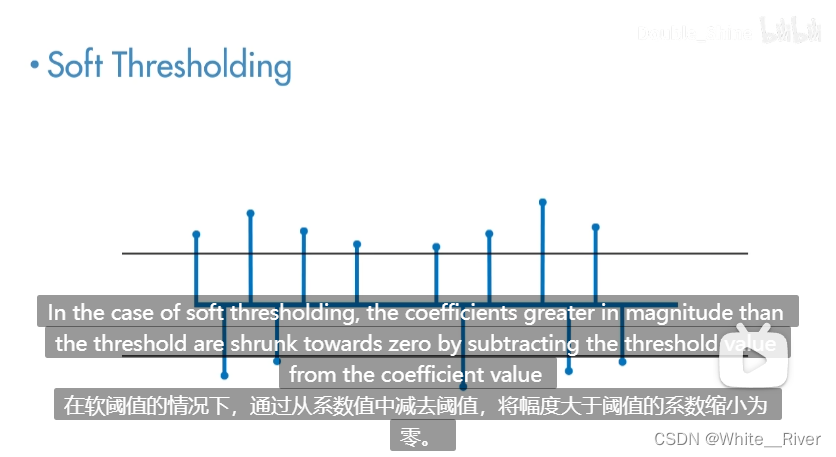
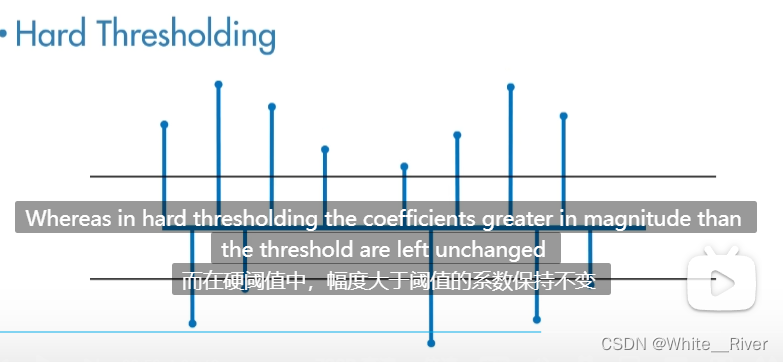
阈值计算技术



傅里叶变换不能告诉我们,这个频率在哪个时间段出现,所以其实本质上只适用于平稳信号(stationary signal)
从系统上来理解就是时不变系统 autonomous system
局部信号指的是被限制在特定区域或范围内的信号。它被包含在一个有限的范围或覆盖区域内,不会超出该边界。这个术语通常在无线通信或信号处理的背景下使用,其中信号需要被限制在特定的地理位置或目标受众中。通过局部化信号,可以将其定向和集中在特定的区域或用户群体上,从而优化通信或传输的效率和有效性。

短时傅里叶变换的数学表示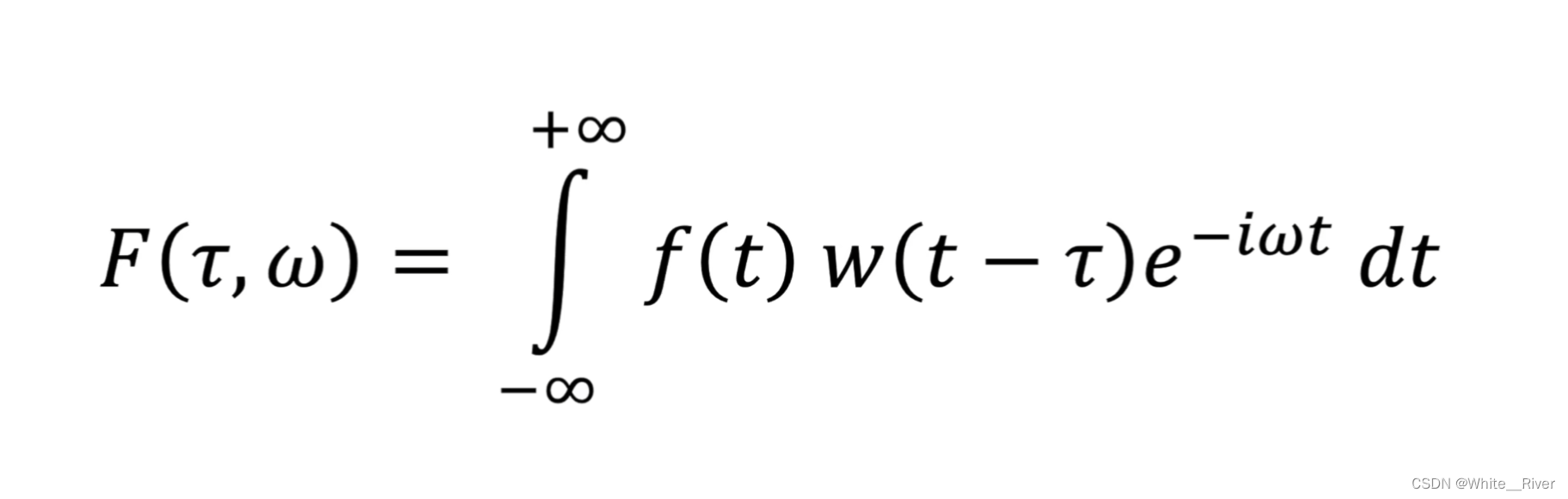
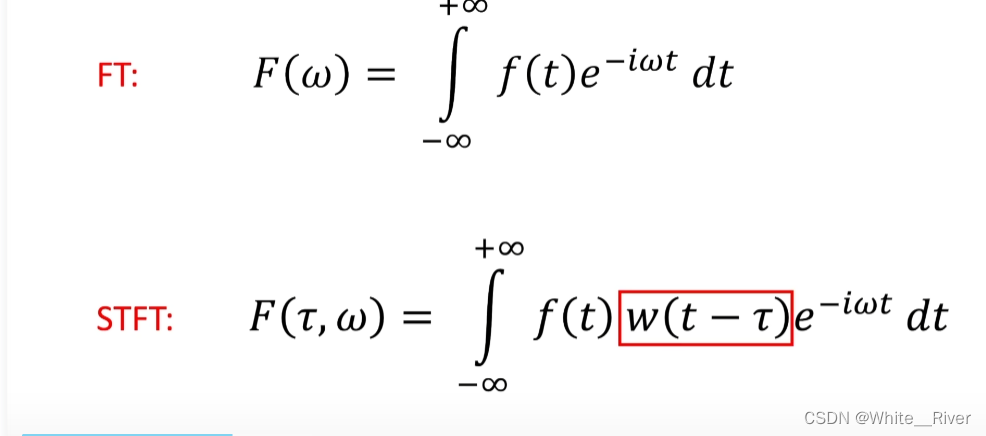
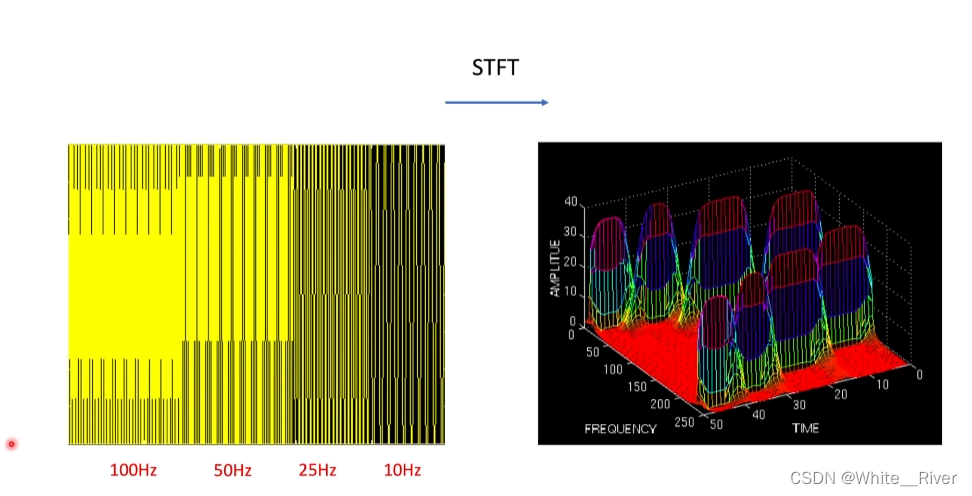
这个图可以显而易见地看出短时傅里叶变换相比传统傅里叶变化的优势和缺点
优势 可提供联合识时频分析
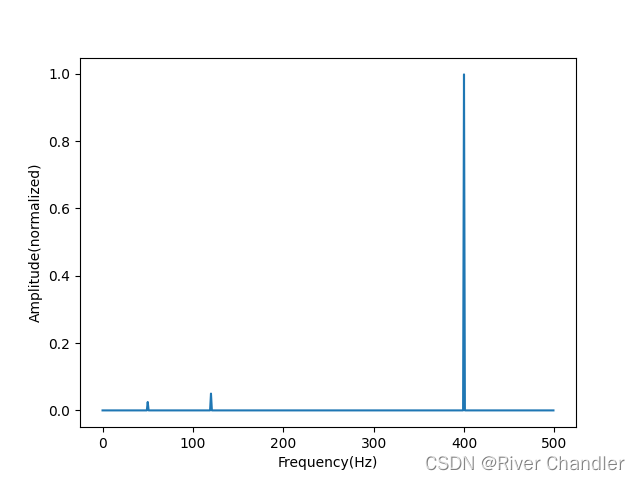
缺点 这是一个很简单的线性调频信号 而且只包含四个频率分量
照理来讲,理想情况是出现四个很尖锐的单峰
但从图上看,显然没有那么“峰”,而是呈现一个比较平滑的分布
所以对于频率分量,或者谐波系数的确定,就存在很大的不确定性
简而言之,就是由于窗函数的窗口长度是一个值,所以一段信号就可以被划分成有限多段, 于是短时傅里叶变化对于频率的分辨率相比传统傅里叶变换就变低了

不确定性定理
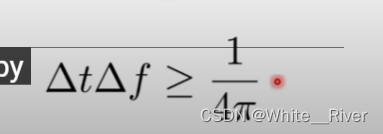

解决方案,根据实际 分而治之

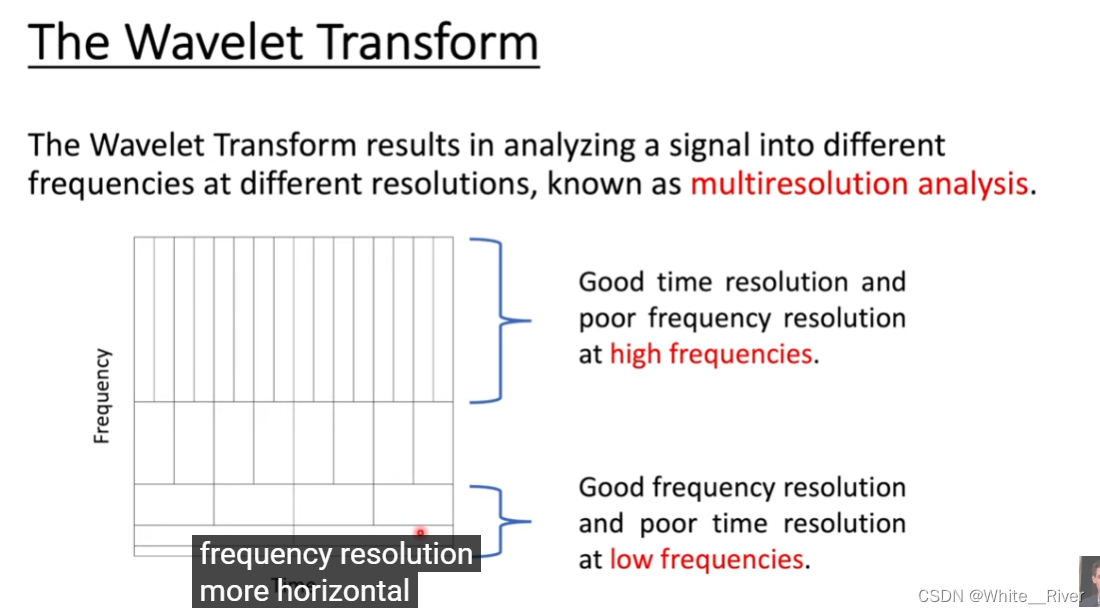
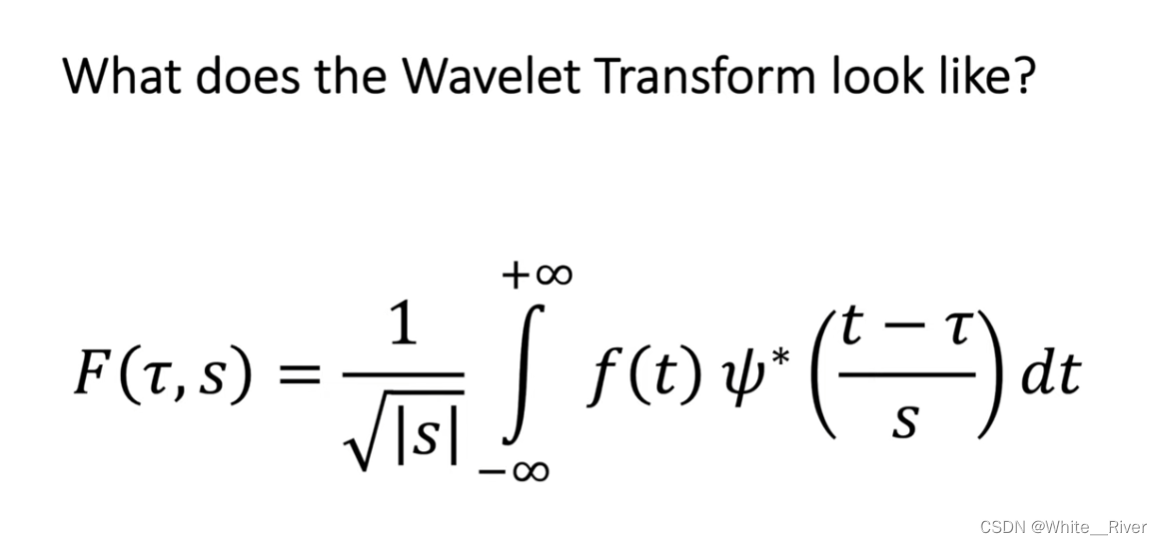



这个大F就是我们的小波系数
小波系数分两种
逼近系数 低频的小波系数
细节系数 高频的小波系数