一、案例介绍

由单因素方差分析案例中，为研究郁金对低张性缺氧小鼠存活时间的影响，将36只小鼠随机生成A、B以及 C 三组，每组12个，雌雄各半，分别以10g/kg、20g/kg、40g/kg三种不同剂量的郁金灌胃，各组小鼠均同时置于放有钠石灰的250ml密闭广口瓶中，观察并记录小鼠存活时间。想要研究不同剂量的郁金下的小鼠的存活时间是否不同，经过分析后发现模型是有显著性差异，说明对个总体均数不全相等，但是究竟是A、B、C三组总体均数全部不等，还是其中两个总体均数不等，需要进一步研究（案例数据来源于：颜虹, 徐勇勇. 医学统计学[J]. 人民卫生出版社, 2015.）。

二、问题分析

经过单因素方差分析后发现模型是有显著性差异，说明对个总体均数不全相等，但是究竟是甲、乙、丙三组总体均数全部不等，还是其中两个总体均数不等，需要进一步对多个均数做两两比较，用多重比较方法。

三、软件操作及结果解读

(一) 数据导入

1.数据格式

首先将数据整理成正确的格式，一般X一列，Y为一例，并且分析的数据带有数据标签的，需要另添加一个表格进行说明，数据格式如下：

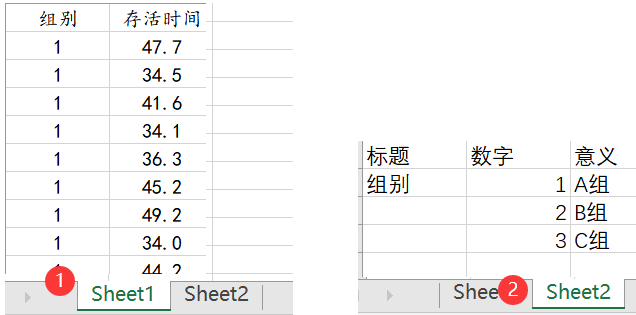
2.导入数据

将整理好的数据上传至SPSSAU系统内，如下：

上传结果如下：

(二)事后多重比较分析

对于单因素方差分析过程，可以参考前面所发的文章，这里对于其相关过程不再赘述。

1. 软件操作
   单因素方差分析后，进行两两比较进一步研究，分析路径为点击【通用方法】→【方差分析】然后进行分析：

1. 事后多重比较方法说明

多重比较有很多种方法，一般根据他的发展所采用的概率分布和发展过程可以发现，一般包括t检验和q检验衍生的方法，目前这两种方法的应用较多，另外还有一些基于F分布的方法，具体说明如下：

（1）LSD方法

LSD是最早的多重比较方法，LSD与独立样本t检验非常相近，主要差别在于LSD法在首先满足F检验达到显著的基础上，将F检验的误差均方作为合并方差，LSD法因其计算简单，检验效能高，所以被广泛应用，有研究者模拟试验比较了不同的事后多重比较方法，发现在方差中F检验显著时，LSD方法是检验效率最高的多重比较方法，但是LSD法也存在明显的不足，比如涉及过多的要比较均数对，犯I型错误的概率较高。其计算公式如下：

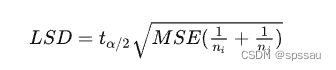
 tα/2为t分布的临界值，通过查t分布表得到，其自由度为n-k，n为样本总数，k为因素中不同水平的水平个数；MSE为组内方差；ni和nj分别为第i个样本和j个样本的样本量。
4.根据显著性水平α做作出决策，如果均值之差的绝对值大于LSD，则拒绝H0，否则不拒绝H0。

（2）Scheffe

Scheffe检验设定所有可能线性组合，Scheffe检验的临界值是用组间自由度乘以F检验的临界值，该方法对于非均衡设计更有效，但是Scheffe计算相较其他方法更为复杂，计算公式如下：

 （3）Bonferroni校正

Bonferroni不等式是指一个或多个时间发生的总概率不高于这些事件各自发生概率的加和。但一般认为该方法过于保守（更难得到拒绝无效假设的结论），Bonferroni法适用于比较次数不是太多的多重比较（比较次数越多越保守）。计算公式如下：

（4）sidak

Sidak基本思路与Bonferroni法接近，一般sidak优于Bonferroni法，它使用Bonferroni修正中的一个特例来估算所有假设测试之间存在的共同显著水平。

（5）Tamhane T2（方差不齐）

如果方差不齐,但希望进行多重比较则使用此方法，其使用前提是需要数据满足正态性，但是不需要满足方差齐性。

（6）SNK Q检验

SNK法的基本目标是把处理均数分成不同处理的子集。这些子集内部都是同质的，但是不同子集之间却存在差异，因此SNK又被称为分层检验，就是按照范围的不同采用不同的检验标准来判定显著性。因为其统计量为q，又称为q检验。其统计量的计算如下：

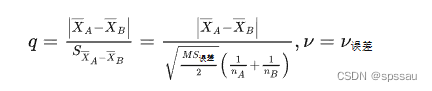
（7）Duncan检验

Duncan氏新复极差法，目前更多的统计学文献不推荐使用该方法，原因在于Duncan多重比较检验误差率的推导是基于单调性条件的（单调上升或单调下降且没有震荡），这也是很多动物试验结果应用Duncan氏新复极差法比较多的原因。

3.进行两两比较

本例子以SNK Q检验进行两两比较。结果如下：

方差分析表格：

SNK Q检验如下:

1. 平均值
   A组和B组比较时平均值就分别是A组数据和B组数据的平均值。其余同理。
2. 差值绝对值

（I）平均值-（J）平均值的绝对值=差值绝对值，比如|40.083-52.985|=12.875,其余以此类推。

3）K

Q检验的界值不但要考虑自由度，还需要考虑秩次R的差别，这里用K进行表示，而A组、B组C组的秩如下：

比如A组和B组：K=|1-2|+1=2；以此类推。

4)df

df为自由度，这里的自由度为误差自由度，一共有3组数据，每组12个样本，所以总的自由度为12×3-1=25，自变量的自由度为3-1=3，所以误差自由度为35-2=33；

5）5％和1％

根据K以及自由度进行查看q检验界值表确定p值。

6）se

Se为差值的标准误，计算如下：

7）LSR值

LSR值=Q临界值*se，比如2.887*1.665=4.792；以此类推；

四、结论

经过单因素方差分析后发现模型是有显著性差异，说明对个总体均数不全相等，经过事后多重比较的SNK Q检验的方法发现A组和B组在0.01水平上呈现显著性，说明两者具有差异，并且A组和C组，B组和C组都是在0.01水平上呈现显著性，说明三者之间两两比较均具有显著性差异。

五、知识小贴士

1、如何做Dunnett法事后多重比较？

如果需要进行Dunnett事后检验法，可使用SPSSAU通用方法里面的非参数检验，并且选择多重比较方法为Dunn’s t法即可。

2、提示‘数据质量异常’如何解决？

如果是X的某个组别下，Y的个数小于2个，此时会出现异常情况。建议使用分类汇总进行检查，确认此种异常情况后，使用筛选样本功能处理后再次分析即可。