介绍
在本文中,我们将看到如何开发具有多个输出的文本分类模型。我们开发一个文本分类模型,该模型可分析文本注释并预测与该注释关联的多个标签。
最近我们被客户要求撰写关于NLP的研究报告,包括一些图形和统计输出。多标签分类问题实际上是多个输出模型的子集。在本文结尾,您将能够对数据执行多标签文本分类。
相关视频:LSTM神经网络架构和工作原理及其在Python中的预测应用
LSTM神经网络架构和原理及其在Python中的预测应用
相关视频:文本挖掘:主题模型(LDA)及R语言实现分析游记数据
文本挖掘:主题模型(LDA)及R语言实现分析游记数据
时长12:59
数据集
数据集包含来自Wikipedia对话页编辑的评论。 评论可以属于所有这些类别,也可以属于这些类别的子集,这是一个多标签分类问题。
现在,我们导入所需的库并将数据集加载到我们的应用程序中。以下脚本导入所需的库:
import pandas as pd
import numpy as np
import re
import matplotlib.pyplot as plt
现在,将数据集加载到内存中:
toxic_comments = pd.read_csv("/comments.csv")
以下脚本显示数据集的维度,并显示数据集的标题:
print(toxic_comments.shape)
toxic_comments.head()
输出:
(159571,8)
数据集包含159571条记录和8列。数据集的标题如下所示:

让我们删除所有记录中任何行包含空值或空字符串的记录。
filter = toxic_comments["comment_text"] != ""
toxic_comments = toxic_comments[filter]
toxic_comments = toxic_comments.dropna()
该comment_text列包含文本注释。
print(toxic_comments["comment_text"][168])
输出:
You should be fired, you're a moronic wimp who is too lazy to do research. It makes me sick that people like you exist in this world.
让我们看一下与此注释相关的标签:
print("Toxic:" + str(toxic_comments["toxic"][168]))
print("Severe_toxic:" + str(toxic_comments["severe_toxic"][168]))
print("Obscene:" + str(toxic_comments["obscene"][168]))
print("Threat:" + str(toxic_comments["threat"][168]))
print("Insult:" + str(toxic_comments["insult"][168]))
print("Identity_hate:" + str(toxic_comments["identity_hate"][168]))
输出:
Toxic:1
Severe_toxic:0
Obscene:0
Threat:0
Insult:1
Identity_hate:0
我们将首先过滤所有标签或输出列。
toxic_comments_labels = toxic_comments[["toxic", "severe_toxic", "obscene", "threat", "insult", "identity_hate"]]
toxic_comments_labels.head()
输出:
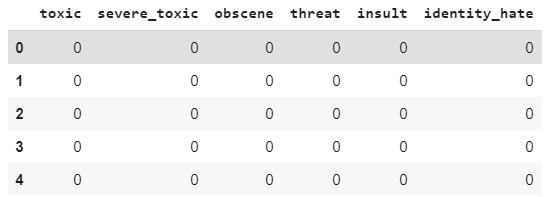
使用toxic_comments_labels数据框,我们将绘制条形图,来显示不同标签的总注释数。
输出:
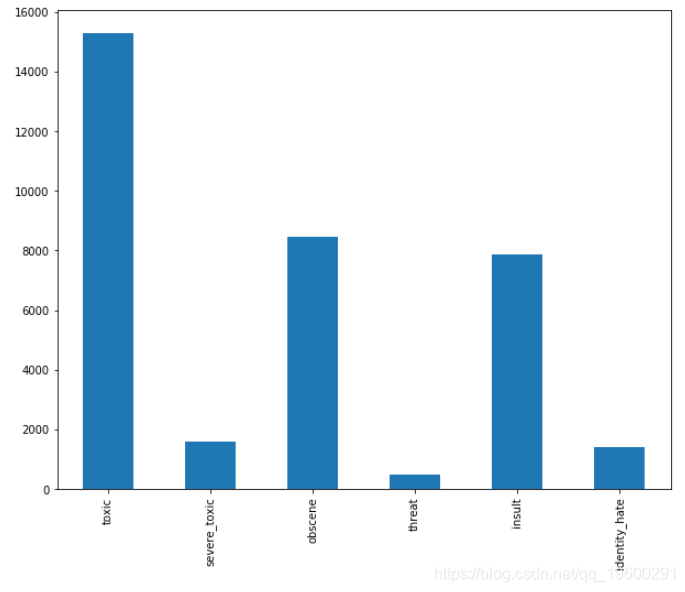
您可以看到,“有毒”评论的出现频率最高,其次是 “侮辱”。
创建多标签文本分类模型
创建多标签分类模型的方法有两种:使用单个密集输出层和多个密集输出层。
在第一种方法中,我们可以使用具有六个输出的单个密集层,并具有S型激活函数和二进制交叉熵损失函数。
在第二种方法中,我们将为每个标签创建一个密集输出层。
具有单输出层的多标签文本分类模型
在本节中,我们将创建具有单个输出层的多标签文本分类模型。
在下一步中,我们将创建输入和输出集。输入是来自该comment_text列的注释。
这里我们不需要执行任何一键编码,因为我们的输出标签已经是一键编码矢量的形式。
下一步,我们将数据分为训练集和测试集:
我们需要将文本输入转换为嵌入式向量。
我们将使用GloVe词嵌入将文本输入转换为数字输入。
以下脚本创建模型。我们的模型将具有一个输入层,一个嵌入层,一个具有128个神经元的LSTM层和一个具有6个神经元的输出层,因为我们在输出中有6个标签。
LSTM_Layer_1 = LSTM(128)(embedding_layer)
dense_layer_1 = Dense(6, activation='sigmoid')(LSTM_Layer_1)
model = Model()
让我们输出模型摘要:
print(model.summary())
输出:
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
input_1 (InputLayer) (None, 200) 0
_________________________________________________________________
embedding_1 (Embedding) (None, 200, 100) 14824300
_________________________________________________________________
lstm_1 (LSTM) (None, 128) 117248
_________________________________________________________________
dense_1 (Dense) (None, 6) 774
=================================================================
Total params: 14,942,322
Trainable params: 118,022
Non-trainable params: 14,824,300
以下脚本输出了我们的神经网络的结构:
plot_model(model, to_file='model_plot4a.png', show_shapes=True, show_layer_names=True)
输出:
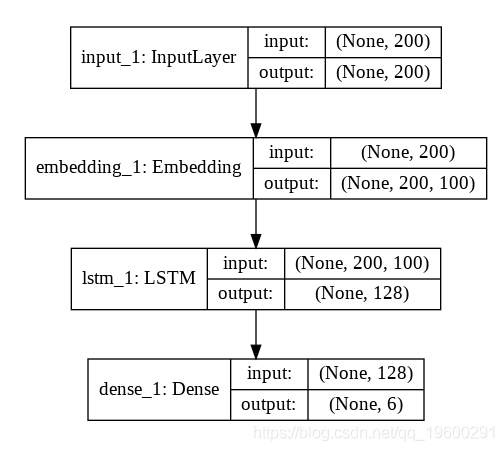
从上图可以看到,输出层仅包含1个具有6个神经元的密集层。现在让我们训练模型:
可以用更多的时间训练模型,看看结果是好是坏。结果如下:
rain on 102124 samples, validate on 25532 samples
Epoch 1/5
102124/102124 [==============================] - 245s 2ms/step - loss: 0.1437 - acc: 0.9634 - val_loss: 0.1361 - val_acc: 0.9631
Epoch 2/5
102124/102124 [==============================] - 245s 2ms/step - loss: 0.0763 - acc: 0.9753 - val_loss: 0.0621 - val_acc: 0.9788
Epoch 3/5
102124/102124 [==============================] - 243s 2ms/step - loss: 0.0588 - acc: 0.9800 - val_loss: 0.0578 - val_acc: 0.9802
Epoch 4/5
102124/102124 [==============================] - 246s 2ms/step - loss: 0.0559 - acc: 0.9807 - val_loss: 0.0571 - val_acc: 0.9801
Epoch 5/5
102124/102124 [==============================] - 245s 2ms/step - loss: 0.0528 - acc: 0.9813 - val_loss: 0.0554 - val_acc: 0.9807
现在让我们在测试集中评估模型:
print("Test Score:", score[0])
print("Test Accuracy:", score[1])
输出:
31915/31915 [==============================] - 108s 3ms/step
Test Score: 0.054090796736467786
Test Accuracy: 0.9810642735274182
我们的模型实现了约98%的精度 。
最后,我们将绘制训练和测试集的损失和准确度,以查看我们的模型是否过拟合。
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train','test'], loc='upper left')
plt.show()
输出:
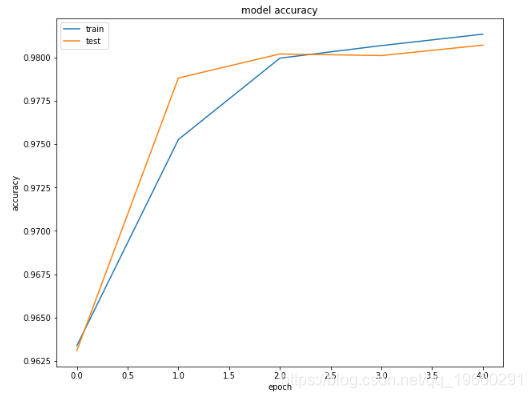
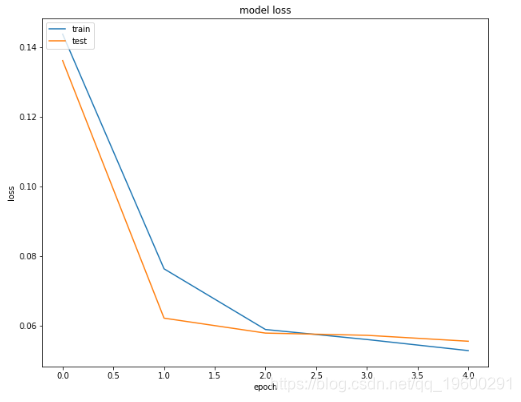
您可以看到模型在验证集上没有过拟合。
具有多个输出层的多标签文本分类模型
在本节中,我们将创建一个多标签文本分类模型,其中每个输出标签将具有一个 输出密集层。让我们首先定义预处理功能:
def preprocess_text(sen):
# 删除标点符号和数字
# 单字符删除
# 删除多个空格
sentence = re.sub(r'\s+', ' ', sentence)
return sentence第二步是为模型创建输入和输出。该模型的输入将是文本注释,而输出将是六个标签。以下脚本创建输入层和组合的输出层:
y = toxic_comments[["toxic", "severe_toxic", "obscene", "threat", "insult", "identity_hate"]]
让我们将数据分为训练集和测试集:
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20, random_state=42)
该y变量包含6个标签的组合输出。但是,我们要为每个标签创建单独的输出层。我们将创建6个变量,这些变量存储来自训练数据的各个标签,还有6个变量,分别存储测试数据的各个标签值。
下一步是将文本输入转换为嵌入的向量。
X_train = pad_sequences(X_train, padding='post', maxlen=maxlen)
X_test = pad_sequences(X_test, padding='post', maxlen=maxlen)
我们将再次使用GloVe词嵌入:
embedding_matrix = zeros((vocab_size, 100))
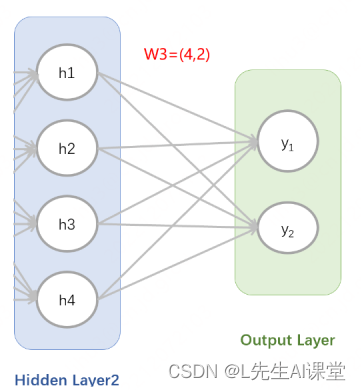
我们的模型将具有一层输入层,一层嵌入层,然后一层具有128个神经元的LSTM层。LSTM层的输出将用作6个密集输出层的输入。每个输出层具有1个具有S型激活功能的神经元。
以下脚本创建我们的模型:
model = Model()
以下脚本输出模型的摘要:print(model.summary())
输出:
__________________________________________________________________________________________________
Layer (type) Output Shape Param # Connected to
==================================================================================================
input_1 (InputLayer) (None, 200) 0
__________________________________________________________________________________________________
embedding_1 (Embedding) (None, 200, 100) 14824300 input_1[0][0]
__________________________________________________________________________________________________
lstm_1 (LSTM) (None, 128) 117248 embedding_1[0][0]
__________________________________________________________________________________________________
dense_1 (Dense) (None, 1) 129 lstm_1[0][0]
__________________________________________________________________________________________________
dense_2 (Dense) (None, 1) 129 lstm_1[0][0]
__________________________________________________________________________________________________
dense_3 (Dense) (None, 1) 129 lstm_1[0][0]
__________________________________________________________________________________________________
dense_4 (Dense) (None, 1) 129 lstm_1[0][0]
__________________________________________________________________________________________________
dense_5 (Dense) (None, 1) 129 lstm_1[0][0]
__________________________________________________________________________________________________
dense_6 (Dense) (None, 1) 129 lstm_1[0][0]
==================================================================================================
Total params: 14,942,322
Trainable params: 118,022
Non-trainable params: 14,824,300
以下脚本显示了我们模型的体系结构:
plot_model(model, to_file='model_plot4b.png', show_shapes=True, show_layer_names=True)
输出:
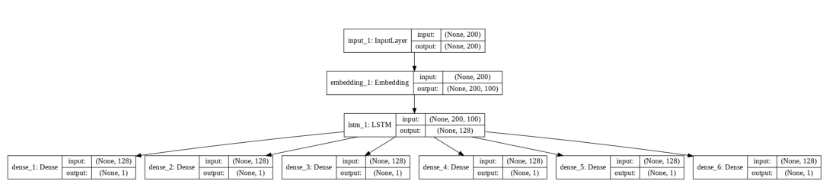
您可以看到我们有6个不同的输出层。上图清楚地说明了我们在上一节中创建的具有单个输入层的模型与具有多个输出层的模型之间的区别。
现在让我们训练模型:
history = model.fit(x=X_train, y=[y1_train, y2_train, y3_train, y4_train, y5_train, y6_train], batch_size=8192, epochs=5, verbose=1, validation_split=0.2)训练过程和结果如下所示:
输出:
Train on 102124 samples, validate on 25532 samples
Epoch 1/5
102124/102124 [==============================] - 24s 239us/step - loss: 3.5116 - dense_1_loss: 0.6017 - dense_2_loss: 0.5806 - dense_3_loss: 0.6150 - dense_4_loss: 0.5585 - dense_5_loss: 0.5828 - dense_6_loss: 0.5730 - dense_1_acc: 0.9029 - dense_2_acc: 0.9842 - dense_3_acc: 0.9444 - dense_4_acc: 0.9934 - dense_5_acc: 0.9508 - dense_6_acc: 0.9870 - val_loss: 1.0369 - val_dense_1_loss: 0.3290 - val_dense_2_loss: 0.0983 - val_dense_3_loss: 0.2571 - val_dense_4_loss: 0.0595 - val_dense_5_loss: 0.1972 - val_dense_6_loss: 0.0959 - val_dense_1_acc: 0.9037 - val_dense_2_acc: 0.9901 - val_dense_3_acc: 0.9469 - val_dense_4_acc: 0.9966 - val_dense_5_acc: 0.9509 - val_dense_6_acc: 0.9901
Epoch 2/5
102124/102124 [==============================] - 20s 197us/step - loss: 0.9084 - dense_1_loss: 0.3324 - dense_2_loss: 0.0679 - dense_3_loss: 0.2172 - dense_4_loss: 0.0338 - dense_5_loss: 0.1983 - dense_6_loss: 0.0589 - dense_1_acc: 0.9043 - dense_2_acc: 0.9899 - dense_3_acc: 0.9474 - dense_4_acc: 0.9968 - dense_5_acc: 0.9510 - dense_6_acc: 0.9915 - val_loss: 0.8616 - val_dense_1_loss: 0.3164 - val_dense_2_loss: 0.0555 - val_dense_3_loss: 0.2127 - val_dense_4_loss: 0.0235 - val_dense_5_loss: 0.1981 - val_dense_6_loss: 0.0554 - val_dense_1_acc: 0.9038 - val_dense_2_acc: 0.9900 - val_dense_3_acc: 0.9469 - val_dense_4_acc: 0.9965 - val_dense_5_acc: 0.9509 - val_dense_6_acc: 0.9900
Epoch 3/5
102124/102124 [==============================] - 20s 199us/step - loss: 0.8513 - dense_1_loss: 0.3179 - dense_2_loss: 0.0566 - dense_3_loss: 0.2103 - dense_4_loss: 0.0216 - dense_5_loss: 0.1960 - dense_6_loss: 0.0490 - dense_1_acc: 0.9043 - dense_2_acc: 0.9899 - dense_3_acc: 0.9474 - dense_4_acc: 0.9968 - dense_5_acc: 0.9510 - dense_6_acc: 0.9915 - val_loss: 0.8552 - val_dense_1_loss: 0.3158 - val_dense_2_loss: 0.0566 - val_dense_3_loss: 0.2074 - val_dense_4_loss: 0.0225 - val_dense_5_loss: 0.1960 - val_dense_6_loss: 0.0568 - val_dense_1_acc: 0.9038 - val_dense_2_acc: 0.9900 - val_dense_3_acc: 0.9469 - val_dense_4_acc: 0.9965 - val_dense_5_acc: 0.9509 - val_dense_6_acc: 0.9900
Epoch 4/5
102124/102124 [==============================] - 20s 198us/step - loss: 0.8442 - dense_1_loss: 0.3153 - dense_2_loss: 0.0570 - dense_3_loss: 0.2061 - dense_4_loss: 0.0213 - dense_5_loss: 0.1952 - dense_6_loss: 0.0493 - dense_1_acc: 0.9043 - dense_2_acc: 0.9899 - dense_3_acc: 0.9474 - dense_4_acc: 0.9968 - dense_5_acc: 0.9510 - dense_6_acc: 0.9915 - val_loss: 0.8527 - val_dense_1_loss: 0.3156 - val_dense_2_loss: 0.0558 - val_dense_3_loss: 0.2074 - val_dense_4_loss: 0.0226 - val_dense_5_loss: 0.1951 - val_dense_6_loss: 0.0561 - val_dense_1_acc: 0.9038 - val_dense_2_acc: 0.9900 - val_dense_3_acc: 0.9469 - val_dense_4_acc: 0.9965 - val_dense_5_acc: 0.9509 - val_dense_6_acc: 0.9900
Epoch 5/5
102124/102124 [==============================] - 20s 197us/step - loss: 0.8410 - dense_1_loss: 0.3146 - dense_2_loss: 0.0561 - dense_3_loss: 0.2055 - dense_4_loss: 0.0213 - dense_5_loss: 0.1948 - dense_6_loss: 0.0486 - dense_1_acc: 0.9043 - dense_2_acc: 0.9899 - dense_3_acc: 0.9474 - dense_4_acc: 0.9968 - dense_5_acc: 0.9510 - dense_6_acc: 0.9915 - val_loss: 0.8501 - val_dense_1_loss: 0.3153 - val_dense_2_loss: 0.0553 - val_dense_3_loss: 0.2069 - val_dense_4_loss: 0.0226 - val_dense_5_loss: 0.1948 - val_dense_6_loss: 0.0553 - val_dense_1_acc: 0.9038 - val_dense_2_acc: 0.9900 - val_dense_3_acc: 0.9469 - val_dense_4_acc: 0.9965 - val_dense_5_acc: 0.9509 - val_dense_6_acc: 0.9900
对于每个时期,我们在输出中的所有6个密集层都有 精度 。
现在让我们评估模型在测试集上的性能:
print("Test Score:", score[0])
print("Test Accuracy:", score[1])
输出:
31915/31915 [==============================] - 111s 3ms/step
Test Score: 0.8471985269747015
Test Accuracy: 0.31425264998511726
通过多个输出层只能达到31%的精度。
以下脚本绘制了第一密集层的训练和验证集的损失和准确值。
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train','test'], loc='upper left')
plt.show()
输出:
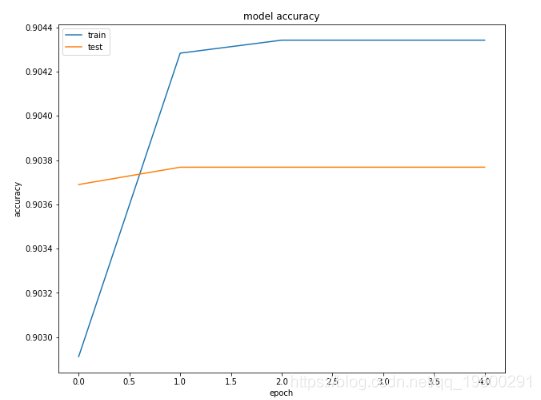
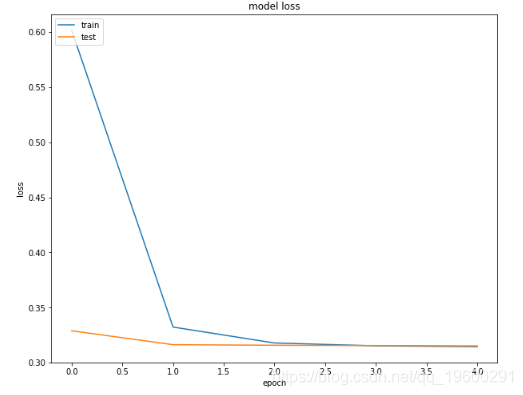
从输出中可以看到,在第一个时期之后,测试(验证)的准确性并未收敛。
结论
多标签文本分类是最常见的文本分类问题之一。在本文中,我们研究了两种用于多标签文本分类的深度学习方法。在第一种方法中,我们使用具有多个神经元的单个密集输出层,其中每个神经元代表一个标签。
在第二种方法中,我们为每个带有一个神经元的标签创建单独的密集层。结果表明,在我们的情况下,具有多个神经元的单个输出层比多个输出层的效果更好。