目录

1.什么是正则化？

2.简化正则化：Lambda

3.两个练习

3.1 问题一

3.2 问题二

4.参考文献

---

1.什么是正则化？

考虑以下泛化曲线，它显示了训练集和验证集相对于训练迭代次数的损失。

图 1. 训练集和验证集的损失

图 1 显示了一个模型，其中训练损失逐渐减少，但验证损失最终上升。换句话说，这条泛化曲线表明模型对训练集中的数据过度拟合。在实践中，通常可以通过惩罚复杂模型来防止过度拟合，这一原则称为正则化（Regularization）。简言之，训练模型不是简单地以最小化损失为目标（经验风险最小化）：

我们现在将【损失+复杂性】最小化，这称为结构风险最小化：

我们的训练优化算法现在是两项的函数：损失项（衡量模型对数据的拟合程度）和正则化项（衡量模型复杂性）。在初级阶段，我们主要关注两种常见（且有些相关）的模型复杂性评估方法：

• 模型复杂性是模型中所有特征权重的函数
• 将模型复杂性作为具有非零权重的特征总数的函数 

如果模型复杂度是权重的函数，则绝对值高的特征权重比绝对值低的特征权重更复杂。我们可以使用  正则化 公式来量化复杂性，该公式将正则化项定义为所有特征权重的平方和：

在这个公式中，接近于零的权重对模型复杂性影响很小，而异常值权重可能会产生巨大的影响。例如，具有以下权重的线性模型：

 正则化项为 26.915：

但 （上面粗体显示）的平方值为 25，几乎贡献了所有的复杂性。所有其他五个权重的平方和仅向  正则化项添加 1.915。

2.简化正则化：Lambda

模型开发人员通过将正则化项的值乘以称为 lambda 的标量（也称为 正则化率）来调整正则化项的整体影响。也就是说，模型开发人员的目标是执行以下操作：

• 鼓励权重值接近 0（但不完全是 0）
• 鼓励权重均值接近 0，呈正态（钟形或高斯）分布。

增加 lambda 值会增强正则化效果。例如，高 lambda 值的权重直方图可能如图 2 所示。

图 2 权重直方图

降低 lambda 值往往会产生更平坦的直方图，如图 3 所示。

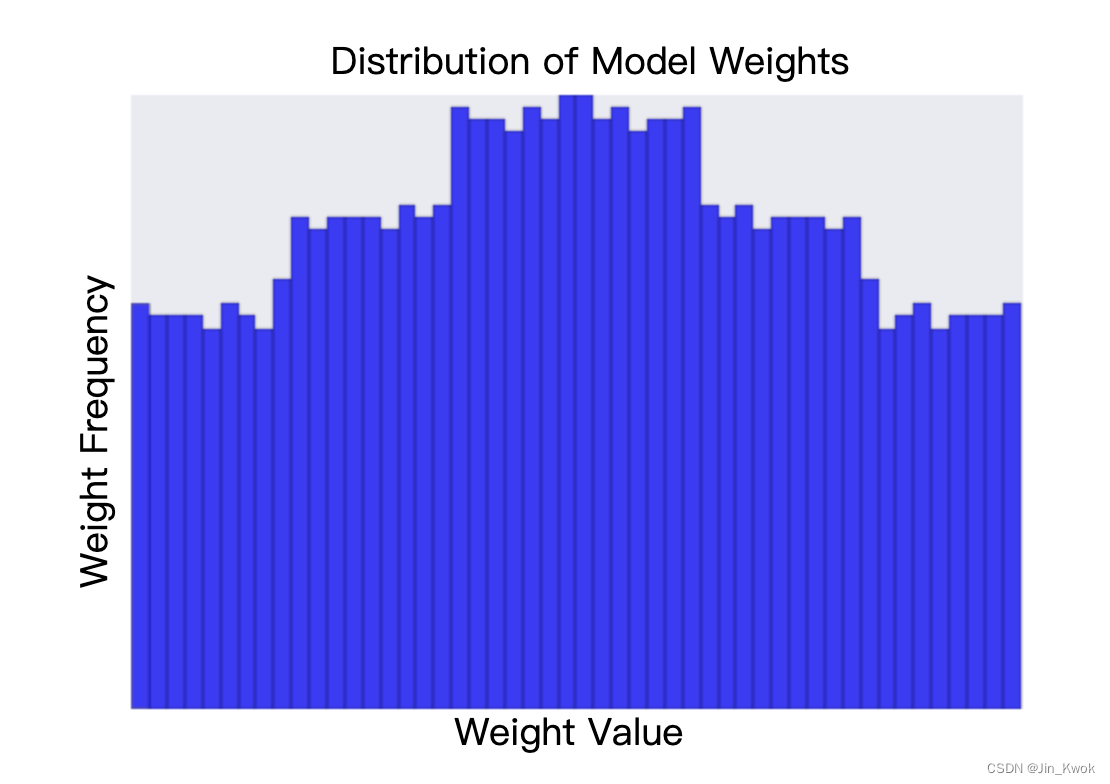
图 3 较低 lambda 值生成的权重直方图

选择 lambda 值时，目标是在简单性和训练数据拟合之间取得适当的平衡：

• 如果 lambda 值太高，虽然模型会很简单，但会面临数据【拟合不足】的风险。最终模型无法充分刻画训练数据，无法做出有用的预测。

• 如果 lambda 值太低，模型将会更加复杂，并且将面临数据【过度拟合】的风险。模型会将训练数据的特殊性也学习到，从而导致泛化能力变差。

注意：将 lambda 设置为零会完全消除正则化。在这种情况下，训练只专注于最小化损失，这会带来最高的过度拟合风险。

理想的 lambda 值生成的模型可以很好地泛化（推广）到新的、以前未见过的数据。不幸的是，理想的 lambda 值取决于数据，因此需要进行一些调整。

3.两个练习

3.1 问题一

4.参考文献

链接-简化正则化：Lambda  |  Machine Learning  |  Google for Developers