12-C++算法笔记-递推

news2024/9/22 4:19:31

📖 引入

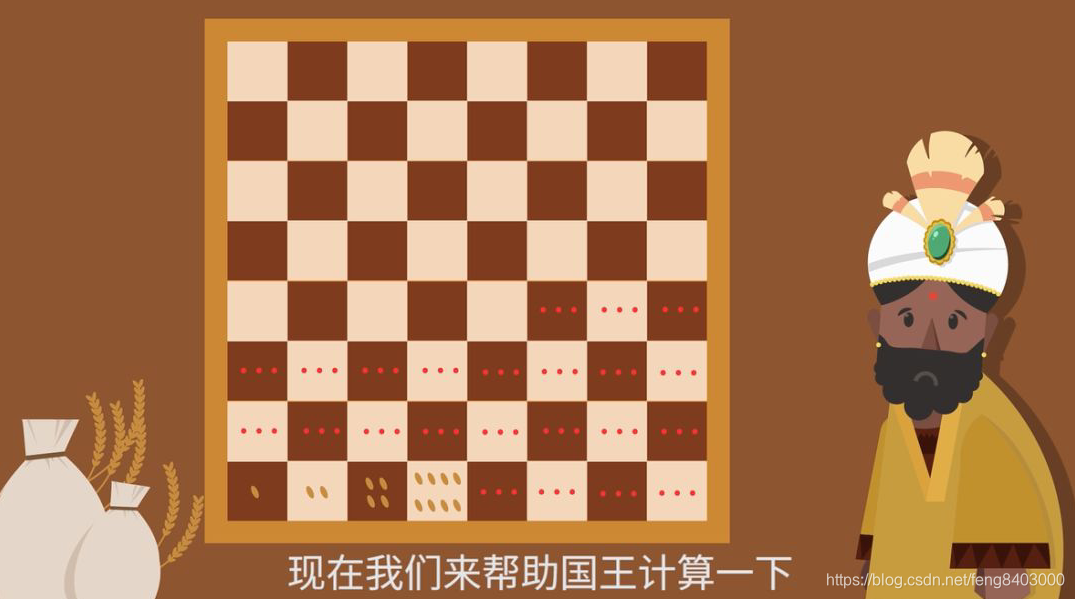
在这里插入图片描述

让我们从一个有趣的例子开始，棋盘放米的问题。假设有一个 $8\times8$ 的棋盘，皇帝想要奖赏一位大臣。大臣提出的要求是在棋盘上按如下规则领赏：第一个格子上放一粒米，随后的每个格子都放置前一个格子上两倍数量的米。

这个问题涉及到一种算法思想，即递推。在递推算法中，我们使用已知的初始条件和递推规则来计算出问题的解。接下来，让我们深入了解递推算法的概念和应用。

📖 什么是递推

递推是一种基于已知条件和规则的算法思想，通过不断利用前面计算的结果来推导出后续的结果。它可以将复杂的问题拆解成简单的子问题，并使用递推规则来解决这些子问题，最终得到问题的解。

递推算法的关键是确定好初始条件和递推规则。初始条件是指已知的起始值，而递推规则则是根据已知值计算下一个值的规则。通过不断迭代应用递推规则，我们可以逐步推导出问题的解。

递推算法常用于处理具有递推关系的问题，例如数列、排列组合、动态规划等。它在编程中具有广泛的应用，能够简化问题的求解过程，并提高算法的效率。

在这里插入图片描述

很多时候，一步登天很难，但如果有个楼梯可以让我们拾阶而上，问题就会变得简单许多。

📖 递推算法练习题

现在，让我们通过两个经典的递推算法练习题来加深对递推算法的理解。

🌟 斐波那契数列

斐波那契数列是指这样的数列：数列的第一个和第二个数都为 1，接下来每个数都等于前面两个数之和。

给出一个正整数 $a$ ，要求斐波那契数列中第 $a$ 个数是多少。

对于斐波那契数列，我们以输入 $a = 7$ 为例，展示推演过程：

月份	第1个数	第2个数	第3个数	第4个数	第5个数	第6个数	第7个数
数值	1	1	2	3	5	8	13

描述：

第一个数和第二个数都为 1，作为斐波那契数列的初始值。
第三个数等于前两个数之和，即 1 + 1 = 2。
第四个数等于前两个数之和，即 1 + 2 = 3。
第五个数等于前两个数之和，即 2 + 3 = 5。
第六个数等于前两个数之和，即 3 + 5 = 8。
第七个数等于前两个数之和，即 5 + 8 = 13。

通过例子推导，可以得到递推式： $F (n) = F (n - 1) + F (n - 2)$ ，其中 $F (n)$ 表示第 $n$ 个斐波那契数。

下面是使用递推算法计算斐波那契数列的代码：

#include <iostream>
using namespace std;

int fibonacci(int n) {
    if (n == 1 || n == 2) {
        return 1;
    }
    int prev = 1;
    int curr = 1;
    for (int i =

 3; i <= n; i++) {
        int temp = curr;
        curr = prev + curr;
        prev = temp;
    }
    return curr;
}

int main() {
    int a;
    cout << "请输入正整数 a：";
    cin >> a;
    int result = fibonacci(a);
    cout << "斐波那契数列中第 " << a << " 个数为：" << result << endl;
    return 0;
}

通过运行上述代码，我们可以输入一个正整数 $a$ ，然后计算并输出斐波那契数列中第 $a$ 个数的值。

🌟 兔子问题

已知有一对兔子，每个月会繁殖一对新的小兔子，新的兔子第二个月会长成成年兔子，能继续进行繁殖。现在想知道过了 $N$ 个月后，总共有多少对兔子？

对于兔子问题，我们以输入 $N = 6$ 为例，展示推演过程：

月份	第1个月	第2个月	第3个月	第4个月	第5个月	第6个月
新生兔子	1	1	1	2	3	5
可以繁殖的兔子对数	0	1	1	2	3	5
总的兔子对数	1	2	2	4	6	10

描述：

第一个月，只有一对兔子，属于新生兔子。
第二个月，还是只有一对兔子，属于可以繁殖的兔子对数。
第三个月，第一对兔子长大并开始繁殖，所以有一对新生兔子，仍然只有一对可以繁殖的兔子。
第四个月，第一对兔子继续繁殖，产生了一对新生兔子，第二对兔子长大并开始繁殖，所以有两对可以繁殖的兔子。
第五个月，第一对兔子和第二对兔子继续繁殖，每对兔子都产生了一对新生兔子，第三对兔子长大并开始繁殖，所以有三对可以繁殖的兔子。
第六个月，第一对兔子、第二对兔子和第三对兔子继续繁殖，每对兔子都产生了一对新生兔子，第四对兔子长大并开始繁殖，所以有五对可以繁殖的兔子。

由此可以推得， $f (n) = f (n - 1) + f (n - 2)$ ，问题转换为求斐波那契数列问题，每个月的兔子总数等于前一个月的兔子总数加上两个月前的成年兔子总数。

下面是使用递推算法计算兔子数量的代码：

#include <iostream>
using namespace std;

int rabbit(int n) {
    if (n == 1 || n == 2) {
        return 1;
    }
    int prev1 = 1;  // n-1 个月的兔子数量
    int prev2 = 1;  // n-2 个月的兔子数量
    int curr = 2;  // n 个月的兔子数量
    for (int i = 3; i <= n; i++) {
        curr = prev1 + prev2;
        prev2 = prev1;
        prev1 = curr;
    }
    return curr;
}

int main() {
    int N;
    cout << "请输入经过的月份数 N：";
    cin >> N;
    int result = rabbit(N);
    cout << "经过 " << N << " 个月后，总共有 " << result << " 对兔子" << endl;
    return 0;
}