“中兴捧月”是由中兴通讯面向在校大学生举办的全球性系列赛事活动,致力于培养学生建模编程、创新、方案策划和团队合作能力。今年是在学校的宣传下了解到比赛,最初抱着学习的态度报名了比赛,最终进入了决赛,完成了封闭的开发与赛题提交,本文记录自己在比赛过程中的主要思路及一些感悟。
初赛
赛题描述:
未来纪元,“宇宙地球人”在节假日会进行星际旅游,欣赏不同星球的地貌风光。但由于宇宙辐射大,各个星球的生存环境恶劣,导致自驾游成本很高,为满足打工人对于诗和远方的追求,星际旅游社规划了不同的星际旅游路线,供众多宇宙人做出自己喜欢的选择。每个旅游星球设置多个旅游入境口,可供旅游飞船进出。宇宙存在多个星系,不同星系间过于遥远,短时间内不可能跨星系旅游。现在宇宙局想了解每个旅游路线的年度旅游人数。(已知每个星球每个入境口的进入星球人数和离开星球人数已经被统计。)

已知:
旅游路径:
旅游路径经过的星球入境口,以path_n命名旅游路径,n为路径编号;xx_yy命名入境口,xx为星球,yy为入境口编号,
示例如下:
path_1:22_4,22_2,23_1,23_3
path_2:22_4,22_3,23_2,23_1
路径说明:旅游路径path_1, 经过星球22,从4号入境口进入,2号入境口离开;然后到达星球23,从1号入境口进入,3号入境口离开
星球入境口人数统计:
入境口名:进入人数,出去人数。
示例如下:
22_1:0,0
22_2:0,10
22_3:0,20
22_4:30,0
23_1:10,20
23_2:20,0
23_3:0,10
赛题思路:

同时已知:

本问题即是一个给定端口流量求路径流量的问题
设路径1的人数为 x 1 x_1 x1,路径2的人数为 x 2 x_2 x2

写成矩阵形式

主要求解问题及解决思路:
1方程组的系数矩阵A不是方阵,列数大于行数,是超定方程组超定方程常用最小二乘法进行求解,即通过最小化残差平方和来找到解。
2根据题目要求,要控制算法的时间复杂度及空间复杂度矩阵A中零元素居多,采用稀疏矩阵进行存储及计算可提升算法效率及减小空间存储
实现方法:
最小二乘法求解超定方程组:
设Ax=b是一个超定方程组,其中A为m行n列的矩阵(m<n),b为m维向量,x为n维向量。对于该方程组的任意一个解
x
0
x_0
x0,定义其残差为:
r
=
b
−
A
x
0
r = b − Ax_0
r=b−Ax0
残差表示方程组的解与实际值之间的误差。最小二乘法的思想就是寻找一个最优解x*,使得其残差平方和最小,即:
‖
r
‖
2
=
‖
b
−
A
x
∗
‖
2
‖r‖^2=‖b − Ax^∗‖^2
‖r‖2=‖b−Ax∗‖2
将残差平方和展开,可以得到:
‖
r
‖
2
=
(
b
−
A
x
∗
)
T
(
b
−
A
x
∗
)
=
b
T
b
−
2
x
∗
T
A
T
b
+
x
∗
T
A
T
A
x
∗
‖r‖^2=(b − Ax^∗)^T(b − Ax^∗)= b^Tb−2x^∗TA^Tb+x^∗TA^TAx^∗
‖r‖2=(b−Ax∗)T(b−Ax∗)=bTb−2x∗TATb+x∗TATAx∗
为了求解最优解x*,我们需要对残差平方和进行求导,并令其等于0。即:
∇
‖
r
‖
2
=
−
2
A
T
(
b
−
A
x
∗
)
=
0
∇‖r‖^2=−2A^T(b − Ax^∗)=0
∇‖r‖2=−2AT(b−Ax∗)=0
解得:
x
∗
=
(
A
T
A
)
−
1
A
T
b
x^∗=(A^TA)^−1 A^Tb
x∗=(ATA)−1ATb
其中,
(
A
T
A
)
−
1
(A^TA)^−1
(ATA)−1
A
T
A^T
AT是A的伪逆矩阵(广义逆矩阵),可以用来求解超定方程组的最小二乘解。但由于题目中的数据量较大,求伪逆矩阵较为耗时,故采取迭代算法.
LSQR 是一种迭代算法,目标是在残差和解向量的误差相等的条件下,找到最小二乘解。 LSQR是利用 Lanezos 方法求解最小二乘问题的一种投影法。由于在求解过程中用到 QR 因子分解,故称最小平方 QR 因子分解法。

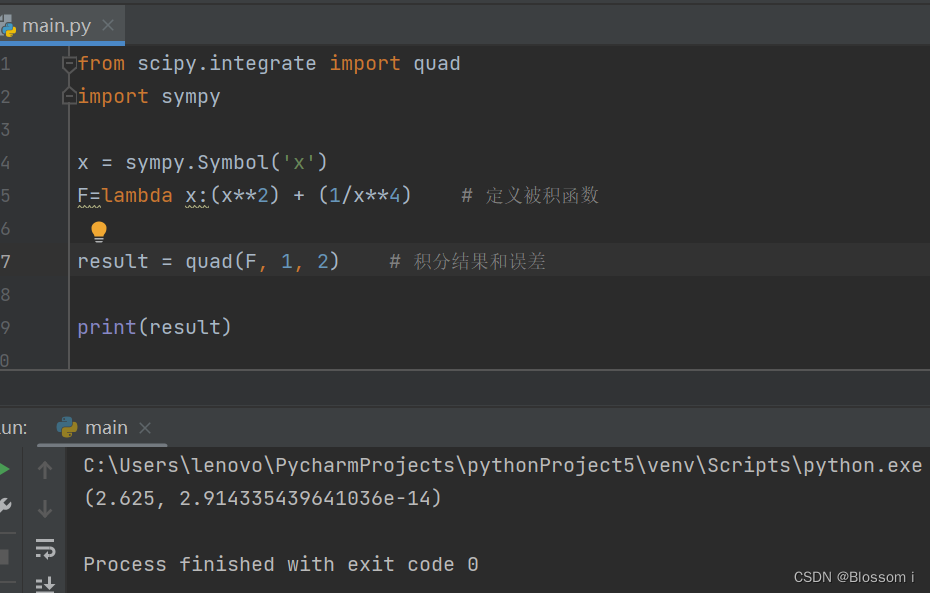
使用python库scipy即可完成求解
from scipy.sparse import csc_matrix
from scipy.sparse.linalg import lsqr
A = csc_matrix([[1., 0.], [1., 1.], [0., 1.]], dtype=float)
b = np.array([0., 0., 0.], dtype=float)
x, istop, itn, normr = lsqr(A, b)[:4]
istop 0
x array([ 0., 0.])
但在求解过程中存在负数解,需要对负数进行约束求解:
非负最小二乘
非负最小二乘(non-negative least squares)是一种优化问题,其目标是在给定约束条件下找到一组非负系数
(
P
)
:
a
r
g
m
i
n
x
≥
0
f
(
x
)
:
=
1
/
2
∥
A
x
−
b
∥
2
2
(P):argmin_{x≥0}f(x):=1/2∥Ax−b∥_2^2
(P):argminx≥0f(x):=1/2∥Ax−b∥22
展开
1
/
2
∥
A
x
−
b
∥
2
2
1/2∥Ax−b∥_2^2
1/2∥Ax−b∥22得到
f
(
x
)
=
1
/
2
(
A
x
−
b
)
T
(
A
x
−
b
)
=
1
/
2
(
x
⊤
A
⊤
A
x
−
x
⊤
A
⊤
b
−
b
⊤
A
x
+
b
⊤
b
)
=
1
/
2
(
x
⊤
A
⊤
A
x
−
2
b
⊤
A
x
+
∥
b
∥
2
2
)
=
1
/
2
x
⊤
A
⊤
A
x
−
b
⊤
A
x
+
1
/
2
∥
b
∥
2
2
.
\begin{array}{cc} f(x)= & 1 / 2(A x-b)^T(A x-b) \\ = & 1 / 2\left(x^{\top} A^{\top} A x-x^{\top} A^{\top} b-b^{\top} A x+b^{\top} b\right) \\ = & 1 / 2\left(x^{\top} A^{\top} A x-2 b^{\top} A x+\|b\|_2^2\right) \\ = & 1 / 2 x^{\top} A^{\top} A x-b^{\top} A x+1 / 2\|b\|_2^2 . \end{array}
f(x)====1/2(Ax−b)T(Ax−b)1/2(x⊤A⊤Ax−x⊤A⊤b−b⊤Ax+b⊤b)1/2(x⊤A⊤Ax−2b⊤Ax+∥b∥22)1/2x⊤A⊤Ax−b⊤Ax+1/2∥b∥22.
令
Q
=
A
⊤
A
,
p
=
(
b
⊤
A
)
⊤
=
A
⊤
b
,
c
=
1
/
2
∥
b
∥
2
2
,
Q=A^⊤A,p=(b^⊤A)^⊤=A^⊤b,c=1/2∥b∥_2^2,
Q=A⊤A,p=(b⊤A)⊤=A⊤b,c=1/2∥b∥22, 非负最小二乘问题转化为一个二次规划:
m
i
n
x
≥
0
1
/
2
x
⊤
Q
x
−
p
⊤
x
+
c
min_{x≥0 }1/2x^⊤Qx−p^⊤x+c
minx≥0 1/2x⊤Qx−p⊤x+c
常数c可忽略,得到:
m
i
n
x
∈
R
+
n
1
/
2
x
⊤
Q
x
−
p
⊤
x
,
Q
=
A
⊤
A
,
p
=
A
⊤
b
min_{x∈ℝ_+^n} 1/2x^⊤Qx−p^⊤x,Q=A^⊤A,p=A^⊤b
minx∈R+n 1/2x⊤Qx−p⊤x,Q=A⊤A,p=A⊤b
梯度投影法:
y
=
x
l
s
=
(
A
T
A
)
−
1
A
T
b
——普通最小二乘法的解
y=x_ls=(A^TA)^−1 A^Tb——普通最小二乘法的解
y=xls=(ATA)−1ATb——普通最小二乘法的解
x = P R + n ( y ) = m a x ( y , 0 ) ——在非负区域的投影 x=P_{ℝ_+^n}(y)=max(y,0)——在非负区域的投影 x=PR+n(y)=max(y,0)——在非负区域的投影
对于方程:
f
(
x
)
=
1
/
2
x
⊤
Q
x
−
p
⊤
x
f(x)=1/2x^⊤Qx−p^⊤x
f(x)=1/2x⊤Qx−p⊤x
梯度为:
∇
f
=
Q
x
−
p
∇f=Qx−p
∇f=Qx−p
投影为:
P
R
+
n
(
x
)
=
[
x
]
+
:
=
m
a
x
(
x
,
0
)
P_{ℝ_+^n}(x)=[x]_+:=max(x,0)
PR+n(x)=[x]+:=max(x,0)
得到算法图

其中: t k t_k tk 步长决定算法的的精度及收敛速度,这里引入Nesterov加速, Nesterov是用于加速梯度下降算法(或其变种)的一种技术。它的主要思想是在更新梯度时,引入一个“动量项”来加速收敛过程。这个动量项是过去一些步骤的平均梯度,它可以帮助算法跳过局部最小值,加速求解全局最小值。

它的求解速度要比nnls快很多:

第一阶段-总流程

第二阶段-总流程

实现效果:

总结:
1.修改了lsqr的收敛判别条件,使其计算速度更快
2.采用了加速投影梯度下降法进行非负最小二乘的求解,在原始非负投影改成区间投影,将负解投影到解的可行空间,保证了解的有效性
3.有针对性的优化,算法仍有很大提升空间(例如一阶段第九组数据对初值较为敏感)
决赛
赛题描述:
假设A君想要从星球甲去往星球乙游玩,他需要乘坐飞船前往。星球停泊口上的飞船按N个班次一轮的规则起飞到下个停泊口,每个班次的飞船最多荷载x人。那么A君就需要选择一个班次的飞船乘坐,飞到一个邻近的星球再选择某个班次的飞船换乘。如此反复换乘之后,最后可以顺利到达星球乙。假设存在大量的游客,他们各自位于不同的起始星球上,想要去往其他星球游览,本套运营系统需要帮他们合理规划飞船换乘路径,并且保证飞船作为公共资源不被大量挤兑也不会被明显浪费。这里A君面临问题包括:
1、如何找到起始地到目的地之间的换乘路径?
2、如果有大量游客同时选择飞船乘坐,如何避免某一班次的荷载高峰?

根据已知数据,得到旅游路线拓扑图

可以看到本题的道路交错复杂,且存在路径交叉点,中转节点较多
赛题思路:
主要问题:
1、如何找到起始地到目的地之间的换乘路径?

可进行遍历查找:

求有向无权图的常用方法是搜索算法:
广度优先搜索(Breadth First Search,BFS ):


•算法效率较低,需要遍历所以节点,直到终点
•空间复杂度高:非常大或者有很多分支,会导致空间占用较高。
迪杰斯特拉算法(Dijkstra):


•基于贪心策略,每次选择当前距离起点最近的节点,并通过该节点更新与它相邻的节点的距离。(本题中,将节点之间的权重设置为1)
2、如果有大量游客同时选择飞船乘坐,如何避免某一班次的荷载高峰?

错峰出行解决拥堵

当班次发生拥堵时:

改换路径解决拥堵

实现方法:

但还要求最大资源利用率以及全局带宽利用率最小化,所以为了降低最大资源利用率,进行容量阈值调整

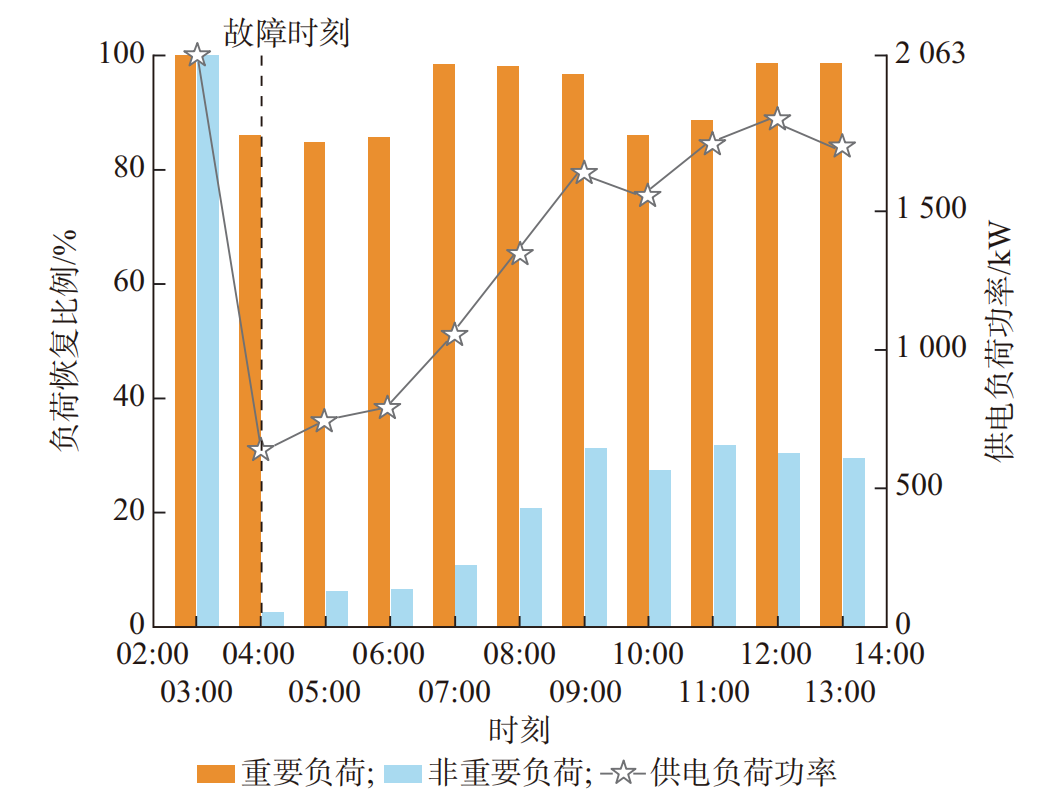
实现效果:

总结:
1.在迪杰斯特拉算法(Dijkstra)的基础上增加运载约束、延误时间约束,保证了路径的可行性与有效性。
2.考虑最大资源利用率以及全局带宽利用率后,引入了班次运载资源约束系数,同时为适应更强的约束条件,在Dijkstra 搜索失败后采用广度优先搜索,保证了在低资源利用率下的路径有效性。
参赛总结
初赛采取线上提交的形式,时间较为充裕,查阅了相关文献并在原有的算法基础上进行了改进,得到了较高得分数,继续优化超参可能分数还会有所提高;决赛在西安线下举行,赛务组准备的很充分,衣食住行各方面考虑的都很周到,还送了水杯、耳塞、眼罩等生活用品,真的很细心。决赛拿到题目的时候还有点不太理解,题目中的对路径的各种约束太多了,评分指标了也有4个,第一天回去后把数据的输入输出接口写好,觉得使用搜索算法是可以将题目求解出来的,但又不想进行这种类似暴力搜索的剪枝求解,看了一些多目标的优化算法,但还是没有什么思路;第二天开始正式的开发,索性先使用搜索算法写一个版本出来,但并没有评判系统(并不是像初赛一样提交可以看到分数,需要将求解数据交给赛道技术人员帮忙跑分)所以就简单写了一个评判系统(这也为我最后数据出现问题却评判失败埋下了种子),使用广度优先搜索速度太慢,又试了试Dijkstra,将节点之间的权重都设置为1,无权图就变成了有权图,速度也得到了较大的提升,下午的时候,可以解出来大部分路径,但在荷载高峰时的判断逻辑还有问题,开发到晚上9点,回到自己住的屋子继续开发,从新梳理了一下思路,把判断逻辑写清楚,所有的路径都可以解出来了,看了评分指标要求最大资源利用率以及全局带宽利用率最小化,这时最大资源利用率为99%,全局带宽利用率为6%,我错误的以为要求最大资源利用率是要求资源利用率尽可能大,看到指标还不错就没有熬夜进行开发,第三天和技术老师交流,才知道自己理解错了,那么主要任务是优化最大资源利用率这个指标,引入了容量阈值,进行约束调整,最终的优化情况三组数据达到了(60%,70%,80%)的最大资源利用率,但在提交数据时却发现第三组数据中一组路径信息是错误的,而我的评判系统漏掉了这条路径,此时距离代码提交不足1个小时的时间,只能回退了一个代码版本,在路径全完成求解的情况下最大资源利用率优化的并不是很好,完成了代码提交。
通过这次参赛,认识到了自己的不足,在解决一个问题时要全方面进行考虑,不能忽略任何一个小细节(评判系统),因为这个小细节可能直接影响成败,同时在参赛过程中结实到了很多优秀的同学,见识了不同的风景,一段很美好的经历,感谢中兴!感谢中兴捧月!