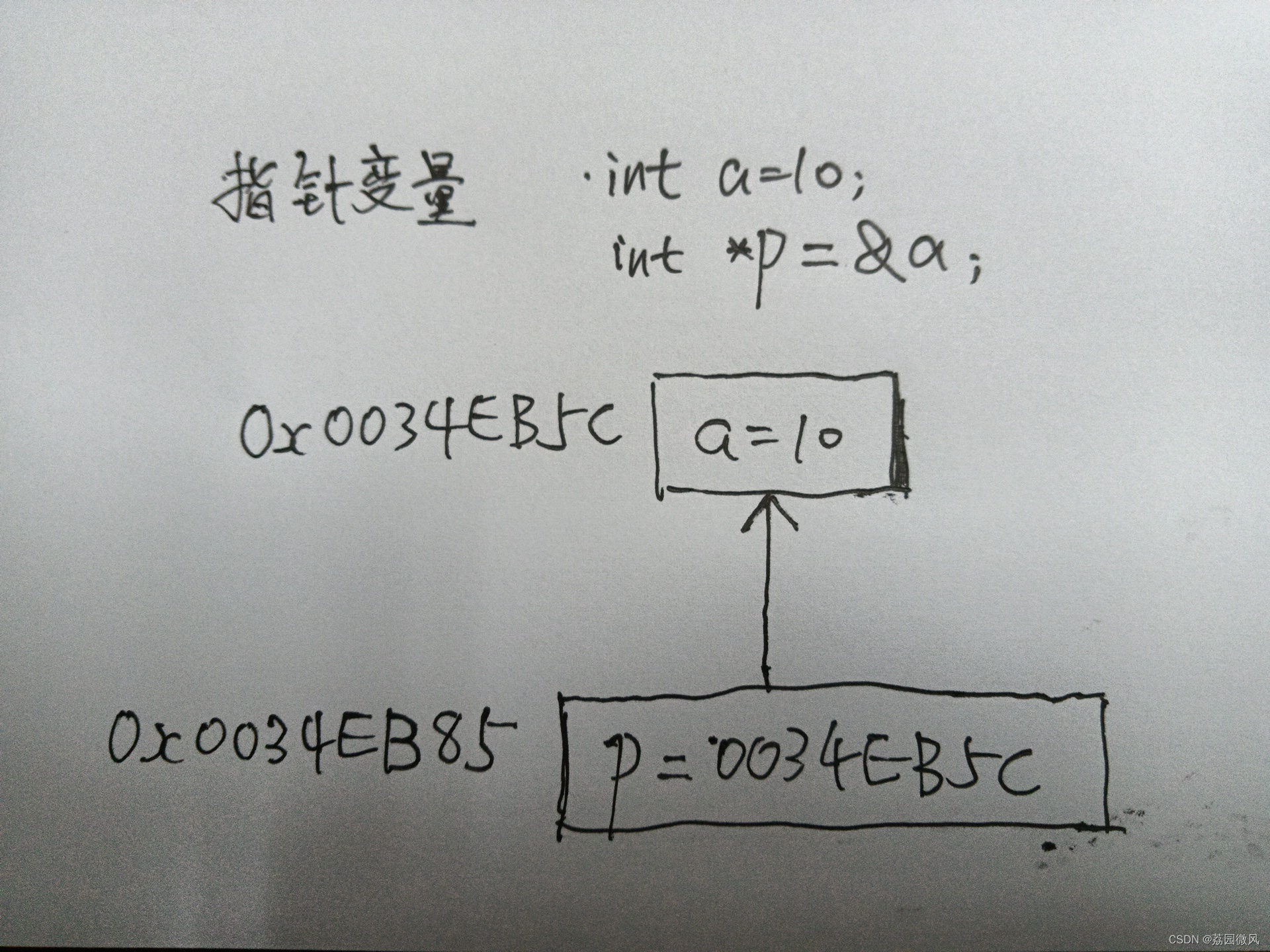
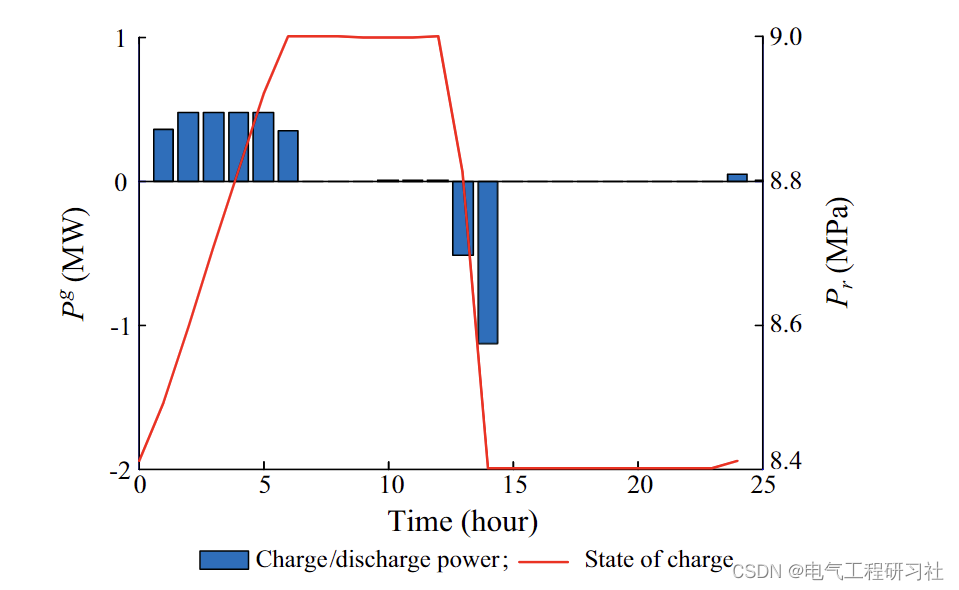
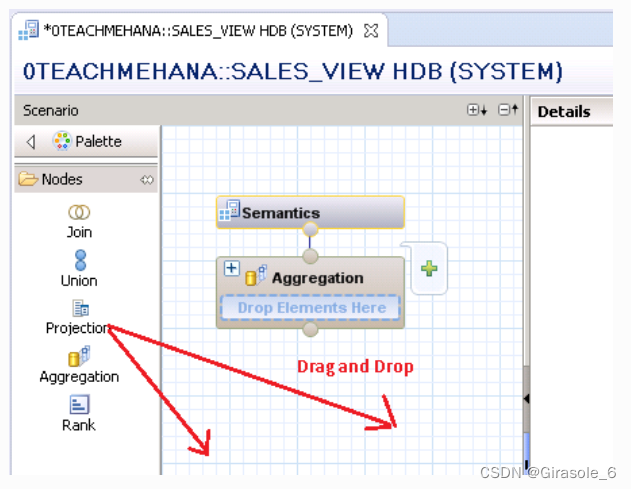
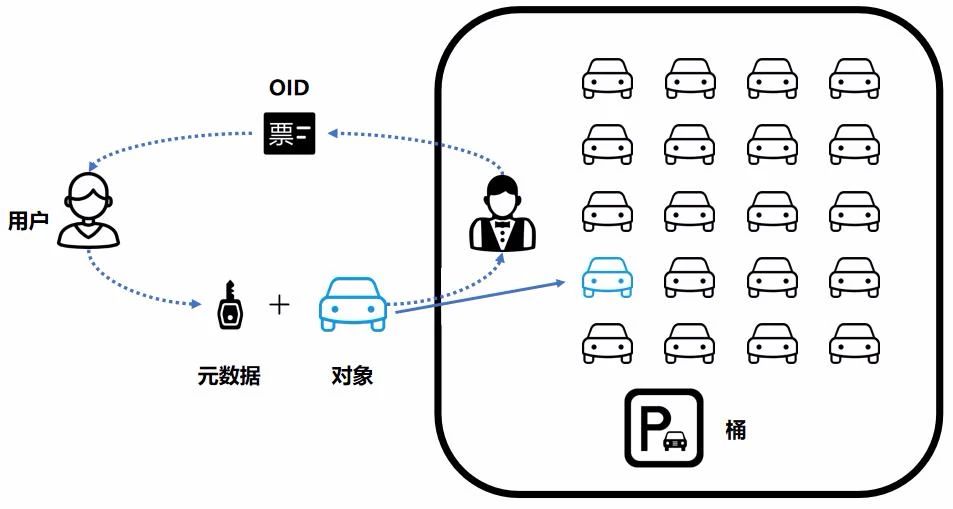
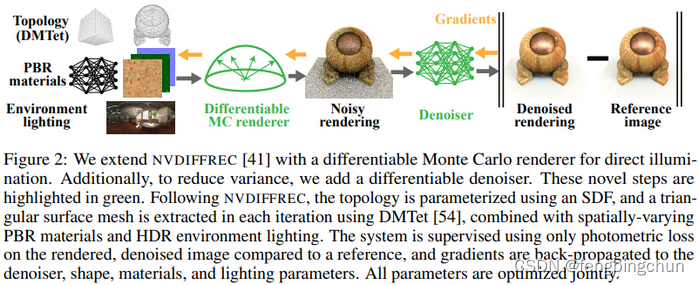
nvdiffrecmc是NVIDIA研究院开源的项目，源代码地址：https://github.com/NVlabs/nvdiffrecmc，论文为《Shape, Light, and Material Decomposition from Images using Monte Carlo Rendering and Denoising》，使用Monte Carlo渲染和去噪对图像进行形状、光照和材质分解，是对nvdiffrec的扩展，输出是triangle mesh和2D纹理，可直接将输出结果导入游戏引擎中：

      Windows上通过Anaconda安装:与nvdiffrec的配置完全一致
      1.安装cuda 11.6
      2.依次执行如下命令：

conda create -n nvdiffrec python=3.9
conda activate nvdiffrec
pip install torch==1.13.1+cu116 torchvision==0.14.1+cu116 torchaudio==0.13.1+cu116 -f https://download.pytorch.org/whl/torch_stable.html
pip install ninja imageio PyOpenGL glfw xatlas gdown
pip install git+https://github.com/NVlabs/nvdiffrast/
pip install --global-option="--no-networks" git+https://github.com/NVlabs/tiny-cuda-nn#subdirectory=bindings/torch
imageio_download_bin freeimage

      3.下载数据集，将Anaconda Powershell Prompt定位到data目录下，执行如下命令：也可根据需要，直接从https://drive.google.com/drive/folders/128yBriW1IG_3NJ5Rp7APSTZsJqdJdfc1 下载

python download_datasets.py

      使用：以lego为例，执行如下命令：比nvdiffrec还耗显存，若显存不够，可减少configs/nerf_lego.json中的batch

python train.py --config configs\nerf_lego.json --display-interval 100

      执行结果如下图所示：

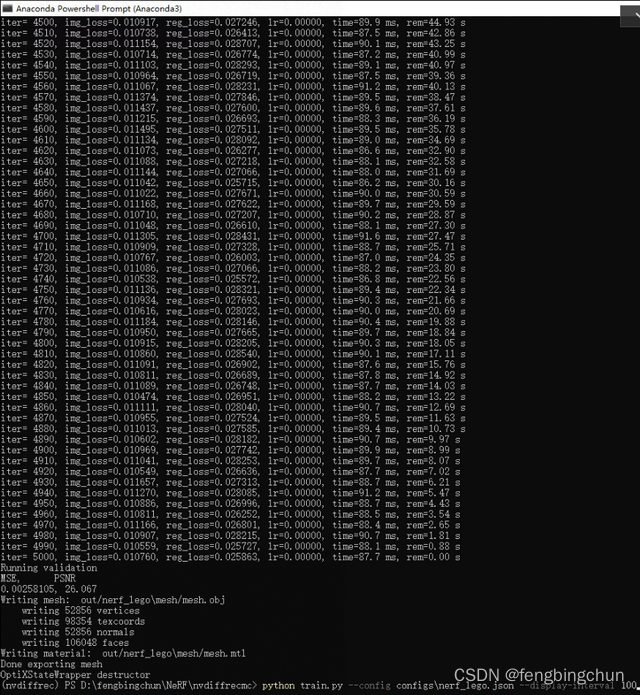
      执行完后会在out/nerf_lego目录下产生一些文件，如下图：我们需要的是mesh目录下产生的6个文件：mesh.obj, mesh,mtl, probe.hdr, texture_kd.png, texture_ks.png, texture_n.png