目录
🍁一.快速排序
🍀Ⅰ.Hoare法
🍇Ⅱ.挖坑法
🍋1.递归版本
🍊2.关于时间复杂度
🍎3.快速排序的优化之三数取中法
🍌4.非递归版本(使用栈实现)
🍐5.非递归的挖坑大法的全部代码
🍑二.冒泡排序(设置flag值)
🍁1.从前往后冒
🏵️2.从后往前冒
🍁一.快速排序
快速排序:英国计算机科学家Tony Hoare于1959年提出。它是基于分治法的思想,具有高效的排序速度和较低的内存消耗。
快速排序的基本思想是通过一个基准元素,将数组分成两个子数组,较小的元素放在左边,较大的元素放在右边,然后对两个子数组递归地进行排序。这样一次划分后,基准元素的位置就已经确定了,它处于最终排序结果的正确位置上。
快速排序的特点是它的平均时间复杂度为O(nlogn),其中n为数组的长度。它具有较低的内存消耗,能够处理大规模的数据集,并且在实践中表现出良好的性能。
由于快速排序的高效性和广泛应用,它成为了经典的排序算法之一,并且在各种编程语言和算法库中被广泛实现和使用。
🍀Ⅰ.Hoare法
Hoare法也就是发明快速排序的大佬以自己名字命名的方法,我也这么牛逼的话(白日做梦,哈哈哈)。
方法的介绍:
1.需要设置一个key值(这个key是下标),一般是数组的第一个位置或者最后一个位置。后面的方法我们都是设置的数组的第一个位置为key值。2.
Ⅰ数组首元素的下标定义为begin,尾元素的下标定义为end,然后我们开始使用a[key]和a[end]的数进行比较,如果a[end]的值大于或者等于a[key]的值,那么这个end位置的值就不动,然后end--,继续找小于a[key]的值,如果找到了,那么就退出循环。
Ⅱ然后就开始比较a[begin]和a[key]的值,和上述的方法是一样的,如果没找到比a[key]大的数,那么begin就一直++,直到找到了比a[key]小的数,退出循环。
Ⅲ然后就是把begin和end位置的交换。3.然后就是重复上面的操作,直到begin的位置和end的位置重合,退出循环,此时把end的位置的值和key位置的值交换一下,再更新一下key的位置为end(因为现在end和begin位置重合,随便哪个都行)。
4.现在的情况是,key位置左边的值全部比a[key]小,而key位置右边的值全部比a[key]大,这时候我们就要缩小区间,继续上述的操作,直到把数组全部变成有序的,这就需要用到递归了。
动图理解:
代码:
//Hoare法
void QuickSort(int* a, int left, int right)
{ //这里的left和right都是下标
if (left >= right)//递归退出的条件
return;
int begin = left;
int end = right;
int key = begin;//key值为数组首元素的下标
while (begin < end)
{
while(begin < end && a[end] >= a[key])
//必须要写begin<end
{
end--;
}
while (begin < end && a[begin] <=a[key])
{
begin++;
}
Swap(&a[begin], &a[end]);//交换begin和end位置的值
}
Swap(&a[begin], &a[key]);
key = begin;//更新key的位置
QuickSort(a, left, key - 1);
QuickSort(a, key + 1, right);
}关于while循环里面的while循环为什么也要写begin<end,这里我们可以举一个例子,你就可以明白了。

🍇Ⅱ.挖坑法
🍋1.递归版本
挖坑法思路讲解:
1.还是一样,选择数组的首元素为pit,也就是为坑。2.然后从最右边的数开始比较,如果大于坑位置的值,就end--,否则就让这个位置的值填到坑的位置,再更新这个位置为坑的位置。
3.然后再继续比较坑和左边的数,和上述操作一样。
4.直到begin和end的位置重合,最后再将end位置的值更新为坑位置的值即可,然后又是递归完成全部的操作。
动图理解:
代码实现:
//挖坑大法
void QuickSort(int* a, int left,int right)
{
if (left >= right)
return;//递归的结束条件
int begin = left;
int end = right;
int pit = begin;
int key = a[pit];
while (begin <end)
{
while (begin < end && key <= a[end])//先找右边的
{
end--;
}
a[pit] = a[end];
pit = end;//更新坑的位置
while (begin < end && key >= a[begin])//再找左边的
{
begin++;
}
a[pit] = a[begin];
pit = begin;
}
pit = begin;
a[pit] = key;//最后把坑的位置给填上
QuickSort(a, 0, pit - 1);
QuickSort(a, pit + 1, right);
}🍊2.关于时间复杂度
关于时间复杂度不是看循环的个数,可能有些老铁理解为,这里的挖坑法while循环里面再嵌套了一个while循环,所以时间复杂度是O(n^2)。这样理解肯定就大错特错了,时间复杂度是看执行的次数,而不是循环的多少个来决定的。
在还没有递归前,循环就是走到begin和end的位置重合即结束,所以就是遍历完了数组,次数就是数组的长度N。
在平均情况下,快速排序的时间复杂度也为O(nlogn)。这是因为快速排序的思想是通过不断地划分和排序子数组来实现整个数组的排序,每次划分可以将一个规模为n的问题划分成两个规模约为n/2的子问题。根据主定理,递归树中每层的总时间复杂度为O(n),递归树的高度为O(logn),因此整个排序的时间复杂度为O(nlogn)。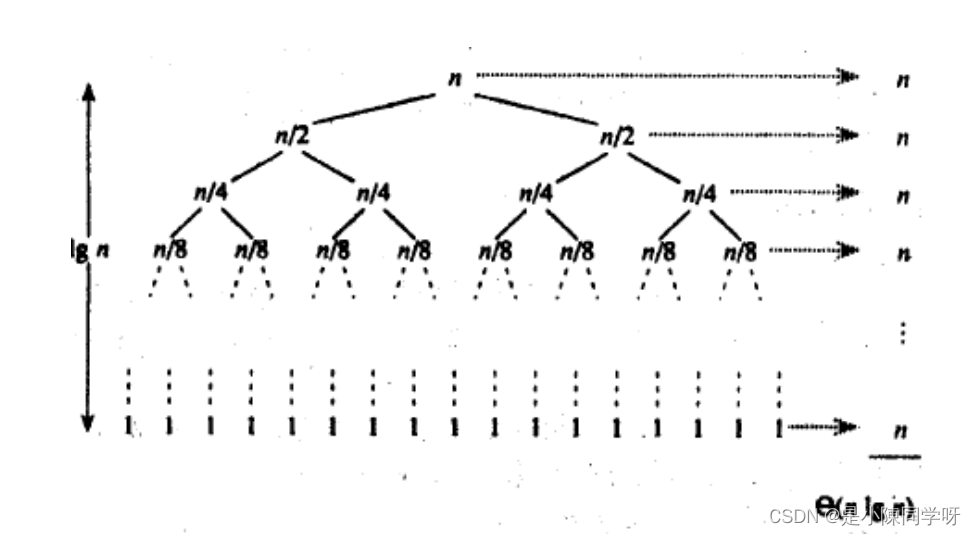
但是当数组已经是有序了之后,不管是升序还是降序, 时间复杂度会变成O(n^2),这是为什么呢?我们可以画图来理解一下。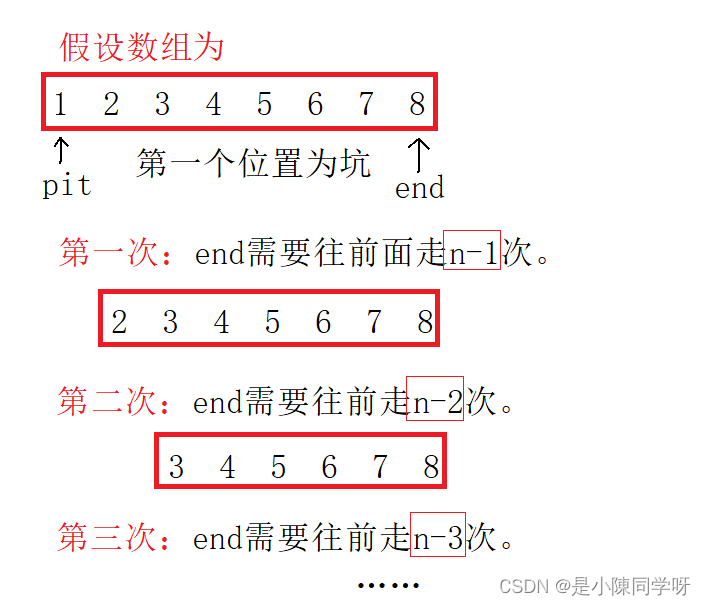
因为有序了之后,就一直不用排左边,一直比较右边,所以次数加起来就是等差数列相加,最坏的时间复杂度就是O(n^2)。那有没有什么办法避免这种情况呢? 接下来就是我们要将的快排的优化。
🍎3.快速排序的优化之三数取中法
之前我们取坑和key的位置都是取的数组的第一个位置,在数组无序的时候确实可以这样取,但是当数组有序了之后,如果你还这样取,坑的位置就是最大或者最小的了,那么就会导致坑这个位置的左端或者右端,永远不会和坑进行比较,这就会导致上述快速排序时间复杂度最坏的情况出现。而三数取中法就可以完美的避开这种麻烦。
三数取中法:
三个数分别是数组的两端和中间的数。也就是在这三个数的中取一个中间大小的数作为坑的位置。这样数组的左右都会和坑进行比较。这样就可以避免数组有序的时候,时间复杂度是O(n^2)。
代码的实现:
int MidSize(int* a, int left, int right)
{
int mid = (left + right) >> 1;
//二进制向左移动一位就是除2的意思,找中间数
while (left < right)
{
if (a[left] > a[mid])
{
if (a[mid] > a[right])
{
return mid;
}
else if (a[right] > a[left])
{
return left;
}
else
{
return right;
}
}
else
{
if (a[right] < a[left])
{
return left;
}
else if (a[right] > a[mid])
{
return mid;
}
else
{
return right;
}
}
}
}这样就可以找到三个数中中间大小的数了。我们还是一样使用第一个位置为坑的位置,只是使用之前先把坑的这个位置和中间大小数的这个位置交换一下,这样就不会存在什么问题了。
int mid = MidSize(a, left, right);
Swap(&a[pit], &a[mid]);🍌4.非递归版本(使用栈实现)
前面我们都是玩的递归法,现在我们来整一个非递归的,递归这么香?为什么还要学习非递归法呢?
这是因为:
递归函数具有很好的可读性和可维护性,但是大部分情况下程序效率不如非递归函数,所以在程序设计中一般喜欢先用递归解决问题,在保证方法正确的前提下再转换为非递归函数以提高效率。
函数调用时,需要在栈中分配新的栈帧,将返回地址,调用参数和局部变量入栈。所以递归调用越深,占用的栈空间越多。如果层数过深,肯定会导致栈溢出,这也是消除递归的必要性之一。
非递归思路:
1.利用栈的先进后出的性质,我们可以先把数组的right入栈,再将left入栈。
2.然后再将依次把栈顶的元素拿出来,所以先把left拿出来,再把right拿出来,这样我们利用一次挖坑法就可以先把坑的左右两端给排好,再利用挖坑法的函数把坑这个位置的下标给返回回来,然后继续把左端和坑的位置-1,坑位置+1和右端依次入栈,上述同样的操作,即可完成非递归的排序。
这里我们是C语言实现的,所以必须自己写一个栈,不像C++,直接有栈的库供我们使用,这就是C语言的弊端所在了,但是没办法,还没学呢?哈哈。
这个非递归的挖坑大法,刚开始不是很好理解,我也看了好几遍,才学会,老铁们也是一样,
反正不急躁,慢慢来,总会搞懂的。
int MidSize(int* a, int left, int right)
{
int mid = (left + right) >> 1;
//二进制向左移动一位就是除2的意思,找中间数
while (left < right)
{
if (a[left] > a[mid])
{
if (a[mid] > a[right])
{
return mid;
}
else if (a[right] > a[left])
{
return left;
}
else
{
return right;
}
}
else
{
if (a[right] < a[left])
{
return left;
}
else if (a[right] > a[mid])
{
return mid;
}
else
{
return right;
}
}
}
}
//挖坑大法
int PartSort(int* a, int left,int right)
{
if (left >= right)
return;//递归的结束条件
int begin = left;
int end = right;
int pit = begin;
int mid = MidSize(a, left, right);
Swap(&a[pit], &a[mid]);
int key = a[pit];
while (begin <end)
{
while (begin < end && key <= a[end])//先找右边的
{
end--;
}
a[pit] = a[end];
pit = end;//更新坑的位置
while (begin < end && key >= a[begin])//再找左边的
{
begin++;
}
a[pit] = a[begin];
pit = begin;
}
pit = begin;
a[pit] = key;//最后把坑的位置给填上
return pit;
}
void QuickSort(int* a, int left, int right)
{
ST st;
StackInit(&st);
StackPush(&st, right);
StackPush(&st, left);
while (!StackEmpty(&st))
{
int begin = StackTop(&st);//出栈顶的元素
StackPop(&st);//
int end= StackTop(&st);
StackPop(&st);
int mid = PartSort(a, begin, end);//返回的mid就坑所在的位置
if (begin < mid - 1)//当begin>=mid-1,那么左区间即排序完毕
{
StackPush(&st, mid-1);//入栈的顺序要区别好,先右再左
StackPush(&st, begin);
}
if (mid + 1 < end)
{
StackPush(&st, end);
StackPush(&st, mid+1);
}
}
StackDestroy(&st);
}🍐5.非递归的挖坑大法的全部代码
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>
typedef int STDataType;
typedef struct Stack
{
STDataType* a;//动态数组
STDataType top;//栈顶
int Capacity;//容量
}ST;
void StackInit(ST* ps)
{
assert(ps);
ps->a = (STDataType*)malloc(sizeof(STDataType) * 4);
if (ps->a == NULL)
{
perror("malloc\n");
return;
}
ps->top = 0;
ps->Capacity = 4;
}
// 入栈
void StackPush(ST* ps, STDataType x)
{
assert(ps);
//判断是否满了
if (ps->top == ps->Capacity)
{
STDataType* temp = (STDataType*)realloc(ps->a, sizeof(STDataType) * ps->Capacity * 2);
if (temp == NULL)
{
perror("realloc\n");
return;
}
ps->Capacity *= 2;//每次增容尾上一次的二倍
ps->a = temp;
}
ps->a[ps->top] = x;
ps->top++;//栈内入一个数据,top就要往上面走一步
}
//出栈
void StackPop(ST* ps)
{
assert(ps);
assert(ps->top > 0);
ps->top--;
}
//判断栈是否为空
bool StackEmpty(ST* ps)
{
assert(ps);
return ps->top == 0;
}
//栈顶的元素是多少
STDataType StackTop(ST* ps)
{
assert(ps);
assert(ps->top > 0);
return ps->a[ps->top - 1];
}
//销毁栈
void StackDestroy(ST* ps)
{
free(ps->a);
ps->a = NULL;
ps->Capacity = 0;
ps->top = 0;
}
void Swap(int* p1, int* p2)
{
int temp = *p1;
*p1 = *p2;
*p2 = temp;
}
int MidSize(int* a, int left, int right)
{
int mid = (left + right) >> 1;
//二进制向左移动一位就是除2的意思,找中间数
while (left < right)
{
if (a[left] > a[mid])
{
if (a[mid] > a[right])
{
return mid;
}
else if (a[right] > a[left])
{
return left;
}
else
{
return right;
}
}
else
{
if (a[right] < a[left])
{
return left;
}
else if (a[right] > a[mid])
{
return mid;
}
else
{
return right;
}
}
}
}
//挖坑大法
int PartSort(int* a, int left,int right)
{
if (left >= right)
return;//递归的结束条件
int begin = left;
int end = right;
int pit = begin;
int mid = MidSize(a, left, right);
Swap(&a[pit], &a[mid]);
int key = a[pit];
while (begin <end)
{
while (begin < end && key <= a[end])//先找右边的
{
end--;
}
a[pit] = a[end];
pit = end;//更新坑的位置
while (begin < end && key >= a[begin])//再找左边的
{
begin++;
}
a[pit] = a[begin];
pit = begin;
}
pit = begin;
a[pit] = key;//最后把坑的位置给填上
return pit;
}
void QuickSort(int* a, int left, int right)
{
ST st;
StackInit(&st);
StackPush(&st, right);
StackPush(&st, left);
while (!StackEmpty(&st))
{
int begin = StackTop(&st);
StackPop(&st);
int end= StackTop(&st);
StackPop(&st);
int mid = PartSort(a, begin, end);
if (begin < mid - 1)//当begin>=mid-1,那么左区间即排序完毕
{
StackPush(&st, mid-1);//入栈的顺序要区别好,先右再左
StackPush(&st, begin);
}
if (mid + 1 < end)
{
StackPush(&st, end);
StackPush(&st, mid+1);
}
}
StackDestroy(&st);
}
void Print(int* a, int n)
{
printf("快速排序后为:\n");
for (int i = 0; i < n; i++)
{
printf("%d ", a[i]);
}
}
int main()
{
int arr[] = { 3,6,8,2,9,5,4,1 };
int n = sizeof(arr) / sizeof(arr[0]);
QuickSort(arr, 0,n-1);
Print(arr, n);
return 0;
}
🍑二.冒泡排序(设置flag值)
🍁1.从前往后冒
冒泡排序是一个非常简单的排序,去年的时候就写过了博客,只是当时还不知道可以设置值来减少冒泡的次数,从而提高效率。
简单的回顾一下思路,冒泡排序中的冒泡就是每次冒泡一个出去,就比如有10个数,我们先把前面的两个数进行比较,如果前面的数大于后面的数,那么它们两个数就进行交换,然后继续后面的数进行比较,10个数只需要交换9次,就可以把最大的一个数给冒泡到数组的末尾。
接着下一次只有9个数交换了,只需要交换8次。最大的也就被冒到最后面了,也就不用管了。
总的就是10个数需要冒9次,冒一次后,交换数的次数也会少一次。
void BubbleSort(int* a, int n)
{ //这里的n是数组的长度,等于8
for (int i = 0; i < n - 1; i++)//8个数需要冒7次,[0-7)总共就是7次
{
int flag = 1;
for (int j = 0; j < n - 1 - i; j++)//冒一次,少一次交换次数
{
if (a[j] > a[j + 1])
{
flag = 0;
//如果没有进入if语句,说明一次都没有交换,即flag恒为1
Swap(&a[j], &a[j + 1]);
}
}
if (flag == 1)//所以flag为真,直接退出循环,冒泡完成
{
break;
}
}
}🏵️2.从后往前冒
void BubbleSort2(int* a, int n)
{
for (int i = 0; i < n-1; i++)
{
int flag = 1;
for (int j = n - 1; j > i; j--)
{
if (a[j] < a[j - 1])
{
flag = 0;
Swap(&a[j], &a[j - 1]);
}
}
if (flag == 1)
{
break;
}
}
}