413. 等差数列划分

点击查看：等差数列划分

---

如果一个数列 至少有三个元素 ，并且任意两个相邻元素之差相同，则称该数列为等差数列。
例如，[1,3,5,7,9]、[7,7,7,7] 和 [3,-1,-5,-9] 都是等差数列。
给你一个整数数组 nums ，返回数组 nums 中所有为等差数组的 子数组 个数。
子数组 是数组中的一个连续序列。

示例 1：
输入：nums = [1,2,3,4]
输出：3
解释：nums 中有三个子等差数组：[1, 2, 3]、[2, 3, 4] 和 [1,2,3,4] 自身。
示例 2：
输入：nums = [1]
输出：0

---

状态转移方程

dp[i]：表示以i位置元素为结尾的所有子数组中等差数列的个数

---

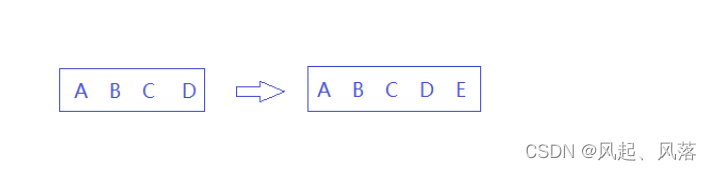
若ABCD为等差数列，而D与B C也能形成等差数列，ABCDE也是一个等差数列

---

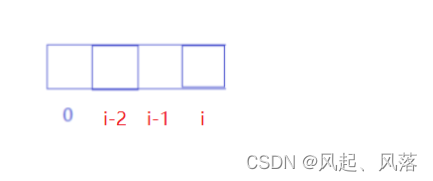
若想求以i为结尾的所有子数组的等差数列的个数，
而子数组是连续的，想要构成等差数列，至少使i位置与 i-1和i-2位置构成等差数列

---

dp[i]分为两种情况

情况1：i i-1 i-2位置元素 可以构成等差数列

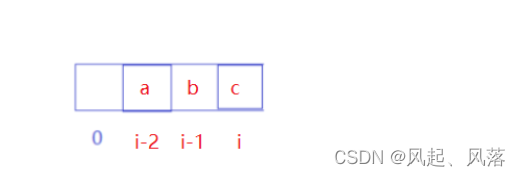
假设i-2位置元素为a，i-1位置元素为b，i位置元素为c
则三者之间的差值相同，即 c-b==b-a

v以a b 为结尾的等差数列 ，由于c 与a b 也能构成等差数列，所以 以 a b c 为结尾也为等差数列
而以 a b为结尾 就相当于 以 b为结尾 即dp[i-1](以i-1位置为结尾的所有等差数列的个数)
而a b c 属于等差数列 ，且不在dp[i-1]的情况之内 ，所以 需要+1

该情况下: dp[i]=dp[i-1]+1

---

情况2：i i-1 i-2位置元素 不构成等差数列

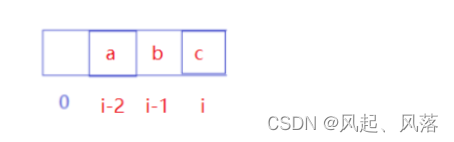
假设i-2位置元素为a，i-1位置元素为b，i位置元素为c
则三者之间的差值不同 即 c-b不等于b-a

因为子数组是连续的，而a b c不构成等差数列，前面构不构成等差数列就没有意义了
该情况下： dp[i]=0

---

状态转移方程为：
dp[i]= c-b==b-a?dp[i-1]+1:0

完整代码

class Solution {
public:
    int numberOfArithmeticSlices(vector<int>& nums) {
         int n=nums.size();
         vector<int>dp(n,0);
         int i=0;
         int sum=0;
         for(i=2;i<n;i++)
         {
             //状态转移方程
             dp[i]=nums[i]-nums[i-1]==nums[i-1]-nums[i-2]?dp[i-1]+1:0;
             sum+=dp[i];
         }
         //返回dp表中所有值之和
         return sum;
    }
};

由于等差数列要求至少有三个元素，当只有一个/两个元素时，不满足要求，所以dp[0]=0 dp[1]=0

978. 最长湍流子数组

点击查看：最长湍流子数组

给定一个整数数组 arr ，返回 arr 的 最大湍流子数组的长度 。
如果比较符号在子数组中的每个相邻元素对之间翻转，则该子数组是 湍流子数组 。
更正式地来说，当 arr 的子数组 A[i], A[i+1], …, A[j] 满足仅满足下列条件时，我们称其为湍流子数组：
若 i <= k < j ：
当 k 为奇数时， A[k] > A[k+1]，且
当 k 为偶数时，A[k] < A[k+1]；
或 若 i <= k < j ：
当 k 为偶数时，A[k] > A[k+1] ，且
当 k 为奇数时， A[k] < A[k+1]。

示例 1：
输入：arr = [9,4,2,10,7,8,8,1,9]
输出：5
解释：arr[1] > arr[2] < arr[3] > arr[4] < arr[5]
示例 2：
输入：arr = [4,8,12,16]
输出：2

---

题目解析

B的值比A大，则呈现上升趋势
C的值比B小，则呈现下降趋势
D的值比C大，则呈现上升趋势
则ABCD数组为湍流子数组

状态转移方程

dp[i]：表示 以i位置为结尾的所有子数组中，最长的湍流数组的长度

刚开始分析写出dp[i]，但是会发现湍流数组有上升和下降趋势的问题，而dp[i]无法解决，所以再次定义f[i]和g[i]

---

f[i]：表示以i位置为结尾的所有子数组中，最后呈现上升趋势的最长湍流数组的长度

---

g[i]：表示以i位置为结尾的所有子数组中，最后呈现下降趋势的最长湍流数组的长度

---

f[i]状态转移方程

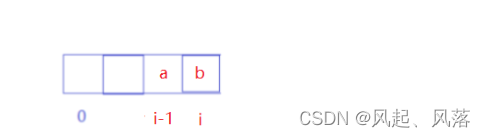
假设i-1位置的元素的值为a，i位置的元素值为b

---

情况1 a>b

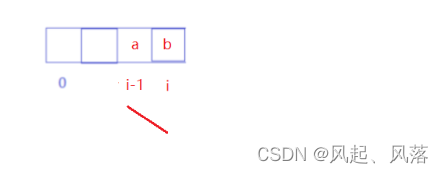
与前面数组结合 只能呈现下降趋势
若想自己呈现上升趋势，单独1个构成子数组，最后一个位置既可以上升，也可以下降
即 f[i]=1

---

情况2 a<b

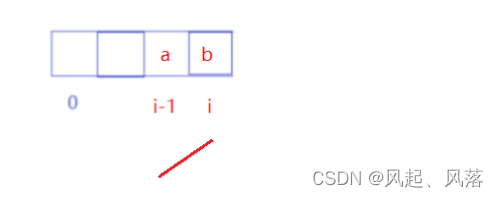
此时呈现上升趋势，符合f[i]的含义

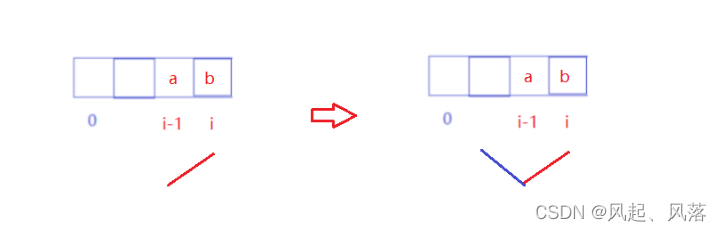
再次寻找以i-1位置为结尾，最后呈现下降趋势的湍流数组的最长的长度 即g[i-1]
再加上由a到b的长度 即+1
该情况下： f[i]=g[i-1]+1

---

情况3 a==b

在该情况下想要使i位置处呈现上升趋势，只能单独1个构成子数组
即 f[i]=1

g[i]状态转移方程

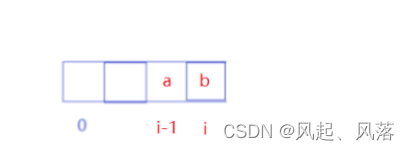
假设i-1位置的元素的值为a，i位置的元素值为b

---

情况1 a>b

此时正好呈现下降趋势， 符合g[i]含义

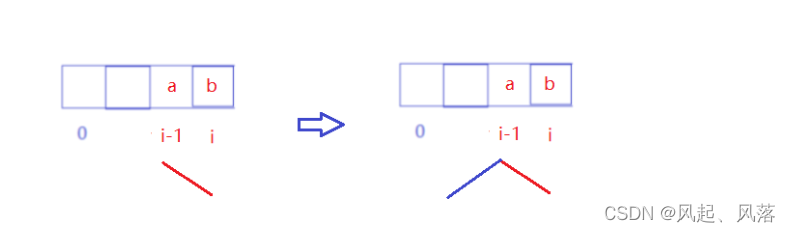
再次寻找以i-1位置为结尾，最后呈现上升趋势的湍流数组的最长的长度 即f[i-1]
再加上由a到b的长度 即+1

该情况下：g[i]=f[i-1]+1

---

情况2 a<b

在该情况下想要使i位置处呈现下降趋势，只能单独1个构成子数组
即g[i]=1

---

情况3 a==b

在该情况下想要使i位置处呈现下降趋势，只能单独1个构成子数组
即g[i]=1

完整代码

class Solution {
public:
    int maxTurbulenceSize(vector<int>& nums) {
       int n=nums.size();
       //f g表 都表示湍流数组的最长长度
       //而单独一个数本身，表示最低长度为1
       //所以f/g 最差长度也为1
       vector<int>f(n,1);
       vector<int>g(n,1);

       int i=0;
       //单独一个数 返回1 ，所以初始值为1
       int fmax=1;
       int gmax=1;
       for(i=1;i<n;i++)
       {
           //f[i] a<b情况
           if(nums[i-1]<nums[i])
           {
               f[i]=g[i-1]+1;
           }
           //g[i] a>b情况
           else if(nums[i-1]>nums[i])
           {
               g[i]=f[i-1]+1;
           }
           fmax=max(fmax,f[i]);
           gmax=max(gmax,g[i]);
       }
       //返回 f和g表中的最大值
       return max(fmax,gmax);
    }
};

单独一个数本身，可以构成上升或者下降趋势 ，所以湍流数组 长度最差也为1
所以可以把f/g表中里面的元素全部初始化为1

139. 单词拆分

点击查看：单词拆分

---

给你一个字符串 s 和一个字符串列表 wordDict 作为字典。请你判断是否可以利用字典中出现的单词拼接出 s 。
注意：不要求字典中出现的单词全部都使用，并且字典中的单词可以重复使用。

示例 1：
输入: s = “leetcode”, wordDict = [“leet”, “code”]
输出: true
解释: 返回 true 因为 “leetcode” 可以由 “leet” 和 “code” 拼接成。
示例 2：
输入: s = “applepenapple”, wordDict = [“apple”, “pen”]
输出: true
解释: 返回 true 因为 “applepenapple” 可以由 “apple” “pen” “apple” 拼接成。
注意，你可以重复使用字典中的单词。
示例 3：
输入: s = “catsandog”, wordDict = [“cats”, “dog”, “sand”, “and”, “cat”]
输出: false

状态转移方程

dp[i]：表示 [0,i]区间内的字符串，能否被字典中的单词拼接而成
若能够拼接而成，则返回true ，若不能则返回false

根据最后一个位置来划分问题

---

若能确定前面这个部分能够拼接成功，并且保证 最后一个单词在字典中，整体字符串就能被拼接而成

设j作为最后一个单词的起始位置的下标
j的范围为 0<=j<=i
0表示整个字符串作为最后一个单词
i表示最后一个字符作为最后一个单词

---

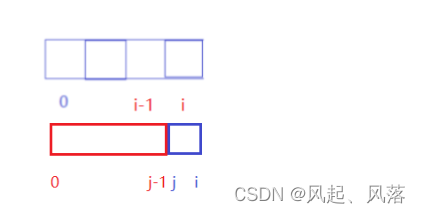
字符串的起始位置为0
j作为最后一个单词的起始位置，所以字符串的终止位置为j-1

[0,j-1]区间内的字符串 需要判断是否能被字典中的单词拼接而成 即dp[j-1]
最后一个单词的范围是 [j,i] ，这段区间内的子串是否在字典中

---

状态转移方程为：
当dp[i-1] 为true 并且 最后一个单词([j-i]范围内)在字典中 两者都满足 ，结果才为true
若有任意一个不成立，则为false

初始化

当j为0时，会发生越界问题

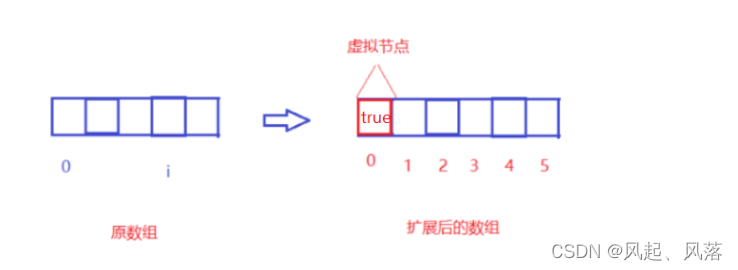
为了防止这种越界问题出现，所以加入一个虚拟节点
扩展后的数组，虚拟节点处下标为0，则 原数组的元素下标从1开始

---

若j为0，表示把0到i这个区间整个看作是最后一个单词，若最后一个单词在字典中，要返回true，
dp[0]=true
这样才能保证两者都为true

---

假设原始字符串为s ，辅助位置一般是空格
s=’ ’ +s
原始字符串加上辅助位置后，原始字符串相当于从1开始计数，正好与新的dp表对应

完整代码

class Solution {
public:
    bool wordBreak(string s, vector<string>& wordDict) {
        unordered_set<string>hash;
        for(auto& s:wordDict)
        {
           hash.insert(s);
        }
         int n=s.size();
         //为了防止越界问题，所以多加一个虚拟节点
         vector<bool>dp(n+1);
         //初始化
         dp[0]=true;
         s=' '+s;//使原始字符串的下标统一+1
         int i=0;
         int j=0;
         for(i=1;i<=n;i++)
         {
             for(j=i;j>=1;j--)
             {
                 //在hash中判断 s中对应的子串在不在 若在返回1 不在返回0
                 if(  dp[j-1]&&  hash.count(s.substr(j,i-j+1)) )
                 {
                     dp[i]=true;
                     break;//找到一种情况即可
                 }
             }
         }
         //因为多加了个虚拟节点，所以下标+1
         return dp[n];
    }
};