文章目录
- 零、总览 / 前言
- 一、冒泡排序
- 1.算法描述
- 2.代码&复杂度
- 二、选择排序
- 1.算法描述
- 2.代码&复杂度
- 三、插入排序
- 1.算法描述
- 2.代码&复杂度分析
- 四、希尔排序
- 1.算法步骤
- 2.代码&复杂度分析
- 五、归并排序
- 1.算法描述
- 2.代码&复杂度分析
- 六、快速排序
- 1.算法描述
- 2.代码&复杂度分析
- 七、堆排序
- 八、计数排序——非比较排序
- 1.算法描述
- 2.代码&复杂度分析
- 九、基数排序——非比较排序
- 十、桶排序——非比较排序
零、总览 / 前言

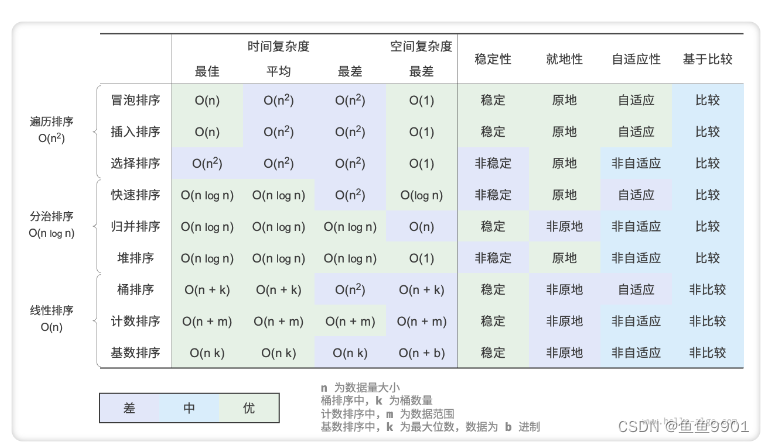
复杂度和稳定性表格一览
| 排序算法 | 平均时间 | 最好时间 | 最坏时间 | 空间 | 稳定性 |
|---|---|---|---|---|---|
| 冒泡 | O ( n 2 ) O(n^2) O(n2) | O ( n ) O(n) O(n) | O ( n 2 ) O(n^2) O(n2) | O ( 1 ) O(1) O(1) | 稳定 |
| 选择 | O ( n 2 ) O(n^2) O(n2) | O ( n 2 ) O(n^2) O(n2) | O ( n 2 ) O(n^2) O(n2) | O ( 1 ) O(1) O(1) | 不稳定 |
| 插入 | O ( n 2 ) O(n^2) O(n2) | O ( n ) O(n) O(n) | O ( n 2 ) O(n^2) O(n2) | O ( 1 ) O(1) O(1) | 稳定 |
| 希尔 | O ( 1 ) O(1) O(1) | 不稳定 | |||
| 归并 | O ( n l o g n ) O(nlogn) O(nlogn) | O ( n l o g n ) O(nlogn) O(nlogn) | O ( n l o g n ) O(nlogn) O(nlogn) | O ( n ) O(n) O(n) | 稳定 |
| 快排 | O ( n l o g n ) O(nlogn) O(nlogn) | O ( n l o g n ) O(nlogn) O(nlogn) | O ( n 2 ) O(n^2) O(n2) | O ( l o g n ) O(logn) O(logn) | 不稳定 |
| 堆排序 | O ( n l o g n ) O(nlogn) O(nlogn) | O ( n l o g n ) O(nlogn) O(nlogn) | O ( n l o g n ) O(nlogn) O(nlogn) | O ( 1 ) O(1) O(1) | 不稳定 |
| 计数排序 | O ( n + k ) O(n+k) O(n+k) | O ( n + k ) O(n+k) O(n+k) | O ( n + k ) O(n+k) O(n+k) | O ( n + k ) O(n+k) O(n+k) | 稳定 |
| 基数排序 | 稳定 | ||||
| 桶排序 | O ( n ) O(n) O(n) | O ( n ) O(n) O(n) | O ( 1 ) O(1) O(1) | 稳定 |
解释一下稳定性:
对于存在相等元素的序列,排序后,原相等元素在排序结果中的 相对位置 相比原输入序列不变 。
例如 nums={3,1,
2
1
2_1
21,
2
2
2_2
22} ,数字 2 出现了两次,下标表示他们出现的次序,若排序方法将 nums 排成了 {1,
2
2
2_2
22 ,
2
1
2_1
21 ,3} ,虽然排序结果正确,但改变了两个 2 的相对位置。只有排序为 {1,
2
1
2_1
21,
2
2
2_2
22,3} 我们才说该排序是稳定的。
如果排序对象只是数值,那么是否稳定没有区别。但若是对引用类型进行排序,排序依据是该类型中的某个可比较的数值字段,那么我们可能会希望该字段相同,但其他字段不同的元素相对位置相比原输入保持不变,这时候就需要稳定排序。
不稳定排序算法
堆排序、快速排序、希尔排序、直接选择排序
稳定排序算法
基数排序、冒泡排序、插入排序、归并排序
一、冒泡排序
1.算法描述
对于要排序的数组,从第一位开始从前往后比较相邻两个数字,若前者大,则交换两数字位置,然后比较位向右移动一位。第1轮从前到后的比较将使得最大的数字 冒泡 到最后
接着第二轮,同样的操作,只不过只需要比到倒数第二个(倒数第一已经最大了)
重复以上操作……
2.代码&复杂度
//冒泡排序,从小到大排序,比较相邻元素,更大的往数组右边移动
static void bubbleSort3(int[] arr)
{
for(int i=arr.length-1;i>0;i--)
{
for(int j=0;j<i;j++)
{
if(arr[j]>arr[j+1])
{
int tmp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = tmp;
}
}
}
}
时间复杂度:O(n^2)
空间复杂度:O(1)
二、选择排序
1.算法描述
步骤:
(1)长度为n的数组中,第一次遍历n-1个数,找到最小的数值与第一个元素交换
(2)第二次遍历n-2个数,找到最小的数值与第二个元素交换
(3)第n-1次遍历,找到最小的数值与第n-1个元素交换,排序完成
2.代码&复杂度
public void selectSort3(int[] arr)
{
for(int i=0;i<arr.length;i++)
{
int minTmp = Integer.MAX_VALUE;
int index=0;
// 开始寻找本轮最小的数字
for(int j=i;j<arr.length;j++)
{
if(minTmp>arr[j])
{
// 每次找到更小的时候记录数字和下标值
minTmp = arr[j];
index = j;
}
}
// 本轮循环结束,将最小值交换到数组前方
int temp = arr[i];
arr[i] = minTmp;
arr[index] = temp;
}
时间复杂度:O(n^2)
空间复杂度:O(1)
三、插入排序
1.算法描述
插入排序是一种最简单直观的排序算法,它的工作原理是通过构建有序序列
算法步骤:
(1)将第一待排序序列第一个元素看做一个有序序列,把第二个元素到最后一个元素当成是未排序序列。
(2)从头到尾依次扫描未排序序列,将扫描到的每个元素插入有序序列的适当位置。如果待插入的元素与有序序列中的某个元素相等,则将待插入元素插入到相等元素的后面。
2.代码&复杂度分析
/*插入排序:从小到大排序,类似于打扑克牌*/
static void insertSort(int[] arr)
{
for(int i=1;i<arr.length;i++)
{
int now=arr[i]; //刚抓的手牌
int j=i-1; //现有最后一张手牌的位置
while (j>=0 && now<arr[j]) //刚抓的手牌小于手上现有的
{
arr[j+1]=arr[j];
j--;
}
arr[j+1]=now;
}
}
时间复杂度:O(n^2)—— i 遍历一次,j遍历了一次,所以n^2
空间复杂度:O(1)—— 原地修改,没有用额外空间
四、希尔排序
1.算法步骤
先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序,待整个序列中的记录"基本有序"时,再对全体记录进行依次直接插入排序。
2.代码&复杂度分析
//希尔排序:从小到大
static void shellSort(int[] arr)
{
for(int interval=arr.length/2;interval>0;interval=interval/2)
{
for(int i=interval;i<arr.length;i++)
{
int temp=arr[i]; //从中间开始
int j=i-interval; //增量是interval的前面的一个元素
while (j>=0 && temp<arr[j])
{
arr[j+interval]=arr[j];
j-=interval;
}
arr[j+interval]=temp;
}
}
}
时间复杂度:
空间复杂度:
五、归并排序
1.算法描述
分而治之,先分治,再合并
2.代码&复杂度分析
public static void main(String[] args) {
int[] arr = {5, 3, 8, 6, 2, 7};
mergeSort(arr, 0, arr.length-1);
System.out.println(Arrays.toString(arr));
}
// 自顶向下,递归实现
public static void mergeSort(int[] arr, int left, int right) {
if (left < right) {
int mid = (left + right) / 2;
mergeSort(arr, left, mid);
mergeSort(arr, mid+1, right);
merge(arr, left, mid, right);
}
}
// 非原地合并
public static void merge(int[] arr, int left, int mid, int right) {
int[] temp = new int[arr.length];
int i = left;
int j = mid + 1;
int k = left;
while (i <= mid && j <= right) {
if (arr[i] <= arr[j]) {
temp[k++] = arr[i++];
} else {
temp[k++] = arr[j++];
}
}
while (i <= mid) {
temp[k++] = arr[i++];
}
while (j <= right) {
temp[k++] = arr[j++];
}
for (int m = left; m <= right; m++) {
arr[m] = temp[m];
}
}
六、快速排序
1.算法描述
首先在数组中确定一个主轴元素 (一般以第一个元素为主轴元素),然后遍历数组,将数组分为两部分, 小于 主轴的元素放在 (最终的) 主轴下标 p 的左侧, 大于等于 主轴的放在右侧。
具体每一轮的操作过程是:
双指针的思想,左指针指向第一个元素,右指针指向最后一个元素。左指针的目标是找到比主轴元素大的,找到后指针就停止,右指针则相反。当两者都找到后,就进行交换。然后继续这个过程,知道两指针相遇。
贴一个简单易懂的快排的排序过程:https://blog.csdn.net/qq_40941722/article/details/94396010
2.代码&复杂度分析
void quickSort(int[] arr,int left,int right)
{
if(left>right)
return;
int pivot=arr[left];
int i=left;
int j=right;
while(i!=j)
{
while (i<j && arr[j]>=pivot)
j--;
while(i<j && arr[i]<=pivot)
i++;
if(i<j)
{
int temp=arr[j];
arr[j]=arr[i];
arr[i]=temp;
}
}
arr[left]=arr[i];
arr[i]=pivot;
quickSort(arr,left,i-1);
quickSort(arr,i+1,right);
}
时间复杂度:O(nlogn)
空间复杂度:O(logn)
七、堆排序
八、计数排序——非比较排序
1.算法描述
计数排序的核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。通常 适用于整数数组,是一种利用整数特点取得 线性复杂度 的非比较排序方法
算法步骤:
(1)找出待排序的数组中最大max和最小min的元素
(2)创建一个计数数组 countArr ,其大小为 arrarr 中的max-min+1
(3)统计数组中每个值为i的元素出现的次数,每读取一个arr[i] ,直接令countArr[arr[i]-min]++
(4) 遍历countArr ,依次输出 counter[i] 个 i ,即为排序结果
2.代码&复杂度分析
static int[] countSort(int[] arr)
{
int minNum=0,maxNum=0;
// 先求出数组中的最大值和最小值
for (int num : arr) {
minNum = Math.min(minNum, num);
maxNum = Math.max(maxNum, num);
}
// 开辟一个新数组:计数数组
int[] count = new int[maxNum-minNum+1];
// 遍历原数组,对应计数数组索引值++
for(int num:arr)
{
count[num-minNum]++;
}
// 开始将计数数组输出
int index=0;
for(int i=0;i<count.length;i++)
{
while(count[i]>0)
{
arr[index++] = i;
count[i]--;
}
}
return arr;
}
时间复杂度: O(n + k),n 为元素个数, k 计数数组大小
空间复杂度:O(k)
上面的还是属于不稳定版本的,稳定版本可以参见:https://leetcode.cn/circle/discuss/eBo9UB/
九、基数排序——非比较排序
十、桶排序——非比较排序
参考链接:https://leetcode.cn/circle/discuss/eBo9UB/