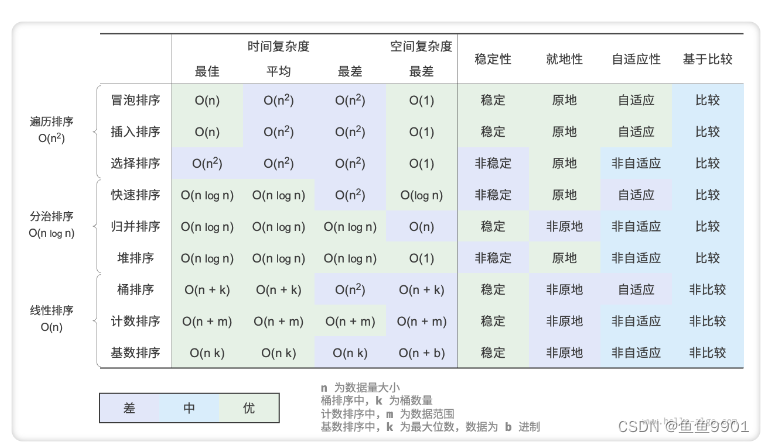
概述：排序算法

在排序算法中，数据类型可以是整数、浮点数、字符或字符串等；顺序的判断规则可根据需求设定，如数字大小、字符 ASCII 码顺序或自定义规则。

评价维度：

运行效率、就地性、稳定性、自适应性（「自适应排序」的时间复杂度会受输入数据的影响，即最佳、最差、平均时间复杂度并不完全相等。如果最差时间复杂度差于平均时间复杂度，说明排序算法在某些数据下性能可能劣化，因此被视为负面属性；而如果最佳时间复杂度优于平均时间复杂度，则被视为正面属性）、通用性。

运行快、原地、稳定、正向自适应、通用性好。显然，迄今为止尚未发现兼具以上所有特性的排序算法。因此，在选择排序算法时，需要根据具体的数据特点和问题需求来决定。

1.选择排序：开启一个循环，每轮从未排序区间选择最小的元素，将其放到已排序区间的末尾。【找的是索引，找到最小元素的索引以后才交换值】

时间复杂度O（n^2)，非自适应排序，空间复杂度O（1），原地排序，非稳定性排序（ 在交换元素时，有可能将 nums[i] 交换至其相等元素的右边，导致两者的相对顺序发生改变）

现实中什么时候会需要规避非稳定性这种情况呢？

在现实中，我们有可能是在对象的某个属性上进行排序。例如，学生有姓名和身高两个属性，我们希望实现一个多级排序：

先按照姓名进行排序：

(A, 180) (B, 185) (C, 170) (D, 170)

接下来对身高进行排序。由于排序算法不稳定，我们可能得到以下结果：学生 D 和 C 的位置发生了交换，姓名的有序性被破坏了，而这是我们不希望看到的。

(D, 170) (C, 170) (A, 180) (B, 185)

2.冒泡排序：通过连续地比较与交换相邻元素实现排序。

从数组最左端开始向右遍历，依次比较相邻元素大小，如果“左元素 > 右元素”就交换它俩。遍历完成后，最大的元素会被移动到数组的最右端。

一共经过n-1轮冒泡结束排序

 如果某轮“冒泡”中没有执行任何交换操作，说明数组已经完成排序，可直接返回结果。

时间复杂度O（n^2)但是加了flag之后，如果输入的是有序数组的话可以达到最佳时间复杂度O（n），也因此它是自适应排序。空间复杂度O（1），原地排序，稳定排序（ 在“冒泡”中遇到相等元素不交换）

3.插入排序：在未排序区间选择一个基准元素，将该元素与其左侧已排序区间的元素逐一比较大小，并将该元素插入到正确的位置。设基准元素为 base ，我们需要将从目标索引到 base 之间的所有元素向右移动一位，然后再将 base 赋值给目标索引。

 时间复杂度O（n^2)但是如果输入的是有序数组的话可以达到最佳时间复杂度O（n），也因此它是自适应排序。空间复杂度O（1），原地排序，稳定排序（在插入操作过程中，我们会将元素插入到相等元素的右侧，不会改变它们的顺序）

插入排序的时间复杂度为 O(n^2)，而即将学习的快速排序的时间复杂度为 O(n log n) 。尽管插入排序的时间复杂度相比快速排序更高，但在数据量较小的情况下，插入排序通常更快。

4.快速排序：选择数组中的某个元素作为“基准数”，将所有小于基准数的元素移到其左侧，而大于基准数的元素移到其右侧。哨兵划分的实质是将一个较长数组的排序问题简化为两个较短数组的排序问题。左侧小于等于基准数小于等于右侧。

注意：哨兵划分这里，以nums[left]作为基准的时候，要先从右往左找首个小于基准数的元素，再从左往右找首个大于基准数的元素

因为先执行从左向右找首个大于基准数的元素的话，i最后会停留在大于基准数的位置，然后再执行找首个小于基准数的元素的时候如果一直没有找到，就会停在j = i 的位置，这个时候交换i 和left 就会把一个大于left的元素交换到最左端了

流程：

1. 首先，对原数组执行一次「哨兵划分」，得到未排序的左子数组和右子数组；
2. 然后，对左子数组和右子数组分别递归执行「哨兵划分」；
3. 持续递归，直至子数组长度为 1 时终止，从而完成整个数组的排序；

 

时间复杂度O（nlogn)，自适应排序（在最差情况下，每轮哨兵划分操作都将长度为 n的数组划分为长度为 0和 n - 1 的两个子数组，使用O（n^2)时间，空间复杂度O（n）（在输入数组完全倒序的情况下，达到最差递归深度 \(n\) ，使用 O(n) 栈帧空间），原地排序，非稳定性排序（在哨兵划分的最后一步，基准数可能会被交换至相等元素的右侧）

为了进一步改进，我们可以在数组中选取三个候选元素（通常为数组的首、尾、中点元素），并将这三个候选元素的中位数作为基准数。

 为了防止栈帧空间的累积，我们可以在每轮哨兵排序完成后，比较两个子数组的长度，仅对较短的子数组进行递归。此这种方法能确保递归深度不超过 log n ，从而将最差空间复杂度优化至 O(log n) 。

 5.归并排序：基于分治思想实现排序，包含“划分”和“合并”两个阶段：

1. 划分阶段：通过递归不断地将数组从中点处分开，将长数组的排序问题转换为短数组的排序问题；
2. 合并阶段：当子数组长度为 1 时终止划分，开始合并，持续地将左右两个较短的有序数组合并为一个较长的有序数组，直至结束；

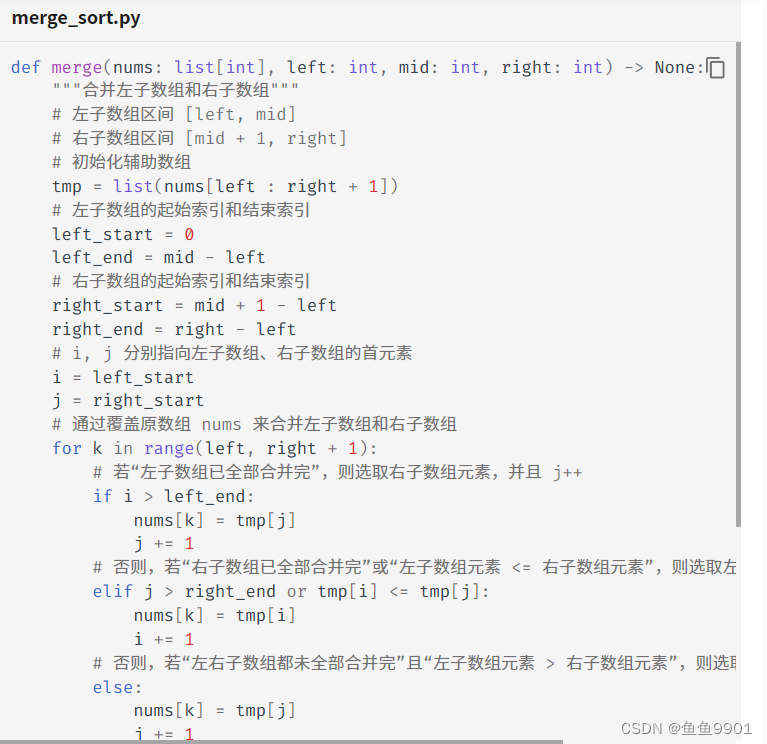
时间复杂度O（nlogn)，非自适应排序，空间复杂度O（n），非原地排序，稳定排序

6.堆排序：是一种基于堆数据结构实现的高效排序算法。

算法流程：

1. 输入数组并建立大顶堆。完成后，最大元素位于堆顶。
2. 将堆顶元素（第一个元素）与堆底元素（最后一个元素）交换。完成交换后，堆的长度减 1 ，已排序元素数量加 1 。
3. 从堆顶元素开始，从顶到底执行堆化操作。完成堆化后，堆的性质得到修复。
4. 循环执行第 2. 和 3. 步。循环 n−1 轮后，即可完成数组排序

 

时间复杂度O（nlogn），非自适应排序，空间复杂度O（1），原地排序，非稳定性排序（在交换堆顶元素和堆底元素时，相等元素的相对位置可能发生变化。） 

7.桶排序：它通过设置一些具有大小顺序的桶，每个桶对应一个数据范围，将数据平均分配到各个桶中；然后，在每个桶内部分别执行排序；最终按照桶的顺序将所有数据合并。

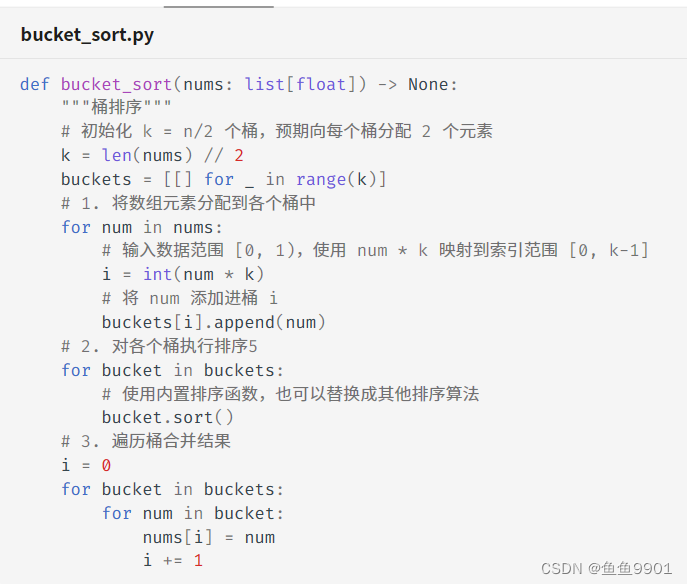
桶排序适用于体量很大的数据， 由于空间限制，系统内存无法一次性加载所有数据。此时，可以将数据分成 1000 个桶，然后分别对每个桶进行排序，最后将结果合并。

时间复杂度O（n+k）（ n个元素，k个桶）自适应排序（在最坏情况下，所有数据被分配到一个桶中，且排序该桶使用 n^2 时间），空间复杂度O（n+k），非原地排序，桶排序是否稳定取决于排序桶内元素的算法是否稳定。

桶排序的时间复杂度理论上可以达到 O(n） ，关键在于将元素均匀分配到各个桶中

8.计数排序：通过统计元素数量来实现排序，通常应用于整数数组。（本质上是桶排序在整形数据下的一个特例，将counter的每个索引可以视为一个桶，将统计数量的过程看做将各个元素分配到对应的桶中）

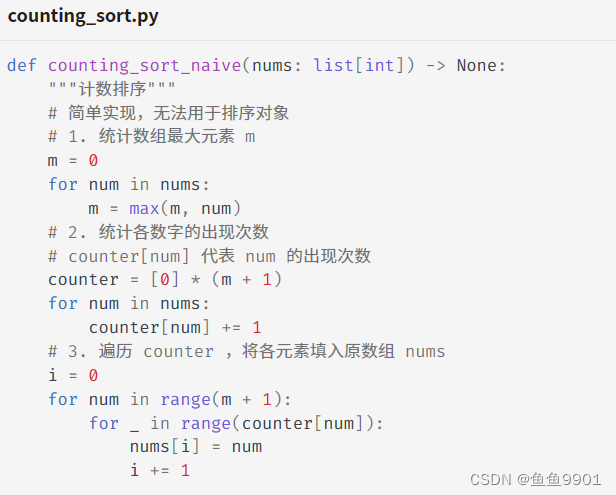
 以下是为了保持稳定性的代码：

 时间复杂度O（n+m），空间复杂度O（n+m），非原地排序，稳定排序

计数排序只适用于非负整数。若想要将其用于其他类型的数据，需要确保这些数据可以被转换为非负整数，并且在转换过程中不能改变各个元素之间的相对大小关系。例如，对于包含负数的整数数组，可以先给所有数字加上一个常数，将全部数字转化为正数，排序完成后再转换回去即可。

计数排序适用于数据量大但数据范围较小的情况。

9.基数排序：核心思想与计数排序一致，也通过统计个数来实现排序。在此基础上，基数排序利用数字各位之间的递进关系，依次对每一位进行排序，从而得到最终的排序结果。

（k从1开始） 

 

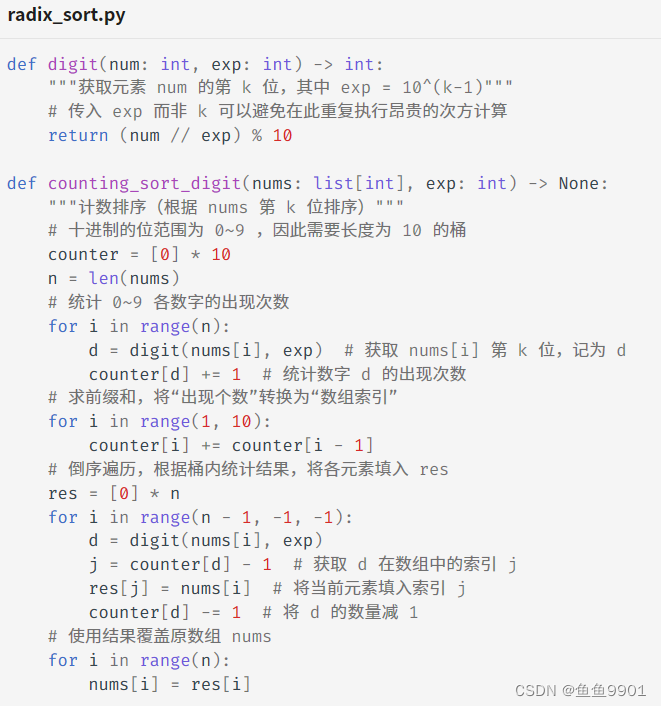
 相较于计数排序，基数排序适用于数值范围较大的情况，但前提是数据必须可以表示为固定位数的格式，且位数不能过大。

时间复杂度O（nk）（最大位数为k），空间复杂度O（n+d）（数据是d进制），非原地排序，稳定排序

这个代码实在是太难了我根本看不懂，只能看懂原理，就先这样吧真的看不懂555

 总结：