目录
🍊一、数据结构概念和分类
🍊二、数组特点&存储方式
🍊三、矩阵
特殊矩阵
非特殊矩阵
🍊四、栈和队列
🍊 五、二叉树的性质
🍊六、二叉树的遍历
(1)前序遍历(先根遍历,先序遍历)
(2)中遍历(中根遍历)
(3)后序遍历(后根遍历,后序遍历)
🍊七、二叉排序树
🍊八、最优二叉树/哈夫曼树
🍊九、完全图和连通图
🍊十、图和矩阵的转化
🍊十一、查找算法
一、数据结构概念和分类
结构:结构是指元素之间的关系。
逻辑结构:元素之间的相互关系称为数据的逻辑结构,可划分为线性结构和非线性结构。
常用的线性结构有:线性表,栈,队列、数组和串。
常见的非线性结构有:二维数组,多维数组,广义表,树(二叉树等),图。
存储结构:数据元素及元素之间关系的存储形式称为存储结构,可分为顺序存储和链接存储两种其本方式。
顺序存储时,相邻数据元素的存放地址也相邻(逻辑与物理统一);要求内存中可用存储单元的地址必须是连续的。
链式存储时,相邻数据元素可随意存放,但所占存储空间分两部分,一部分存放结点值,另一部分存放表示结点间关系的指针。
二、数组特点&存储方式
数组特点:数据元素数目固定。数据元素具有相同的类型。数据元素的下标关系具有上下界的约束且下标有序。
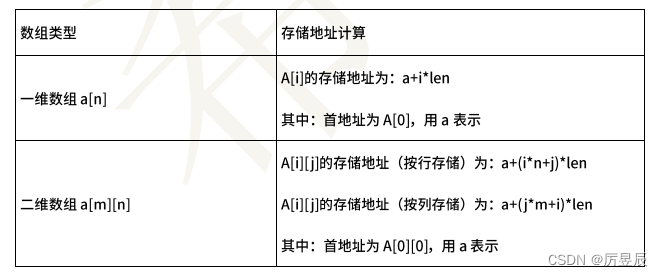
其中:len表示单个元素所占用的存储单元。
三、矩阵
特殊矩阵
三角矩阵:非零元素集中在矩阵的对角线的一边,包括上三角矩阵和下三角矩阵。
对角矩阵:矩阵中的非零元素都集中在以主对角线为中心的带状区域中
对称矩阵/反对称矩阵:Ann中的元素具有ai=ap的特点,则称之为阶对称矩阵。Ann中的元素具有aij=-a的特点,则称之为阶反对称矩阵。
非特殊矩阵
稀疏矩阵:非零元素的个数远远少于零元素的个数,且非零元素的分布没有规律;对于稀疏矩阵,存储非零元素时必须同时存储其位置(即行号和列号),所以三元组(i,i,ai)可唯一确定矩阵中的一个元素。
四、栈和队列
栈是只能在一端进行插入和删除操作的线性表,其中允许插入和删除的一端叫做栈顶,另一端叫做栈底。栈是一种后进先出(LIFO)的数据结构,先入栈的元素要比后入栈的元素后出栈。故将一串数据全部入栈后再全部出栈,数据的次序将前后颠倒。
栈主要应用于函数调用或中断调用过程中。
队列是只能在一端插入,在另一端删除的线性表,其中允许插入元素的一端称为队列头或队头,允许删除元素的一端称为队列尾或队尾。队列是一种先进先出(FIFO)的数据结构,先入队列的元要先于后入队列的元素出队列。故一串数据无论以何种操作次序通过队列,其次序都不会发生变化。
循环队列:
队空条件:head=tail
队满条件:(tail+1)%size=head
队列长度:(tail-head+size)%size
循环队列的优点:入队和出队操作都不需要移动队列中的其他元素
五、二叉树的性质
(1)在二叉树的第i层上最多有2i-1个结点(i≥1);
(2)深度为k的二叉树最多有2k1个结点(k≥1);
(3)叶子结点数为no,度为2的结点数为n2,则no=n2+1
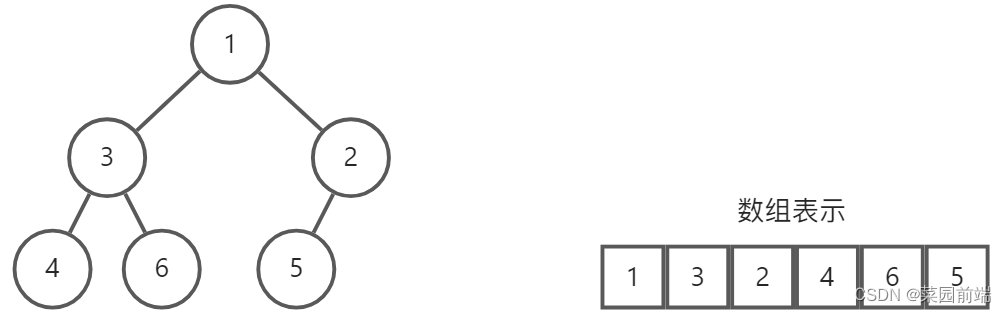
(4)如果对一棵有n个结点的完全二叉树的结点按层序编号(从第1层到Llogn+1层,每层从左到右),
则对任一结点i(1≤i≤n),有:
如果i=1,则结点i无父结点,是二叉树的根;如果i>1,则父结点是Li/2j;
如果2i>n,则结点i为叶子结点,无左子结点:否则,其左子结点是结点2i:
如果2i+1>n,则结点i无右子叶点,否则,其右子结点是结点2i+1。
六、二叉树的遍历
(1)前序遍历(先根遍历,先序遍历)
首先访问根结点,然后前序遍历根结点的左子树,最后再前序遍历根结点的右子树。
(2)中遍历(中根遍历)
首先中序遍历根结点的左子树,然后访问根结点,最后再中序遍历根结点的右子树。
(3)后序遍历(后根遍历,后序遍历)
首先后序遍历根结点的左子树,然后后序遍历根结点的右子树,最后再访问根结点。
二叉树可用来描述算术表达式,此时对二叉树的先序、中序和后序遍历序列分别对应了表达式的前级表示(波兰式)、中缀表示和后缀表示(逆波兰式)。
七、二叉排序树
二叉排序树(BinarySortTree)又称为二叉搜索树,或者是一棵空树,或者是具有下列性质的二叉树:
(1)若左子树不空,则左子树上所有结点的值均小于根结点的值。
(2)若右子树不空,则右子树上所有结点的值均大于根结点的值。
(3)左右子树也都是二叉排序树。
二叉排序树的中序遍历是一个递增的序列。
八、最优二叉树/哈夫曼树
树中连接两个结点之间的分支数目称为此两结点的路径长度,结点的带权路径长度为从树根到该结点之间的路径长度与该结点上权的乘积,树的带权路径长度是指从树的根结点到其他各个结点的路径长度之和,带权路径长度最小的二叉树称为最优二叉树或哈夫曼树。
九、完全图和连通图
完全图:在无向图中,若每对顶点之间都有一条边相连,则称该图为完全图(completegraph)。在有向图中,若每对顶点之间都有二条有向边相互连接,则称该图为完全图。
连通图:指任意两个结点之间都有一个路径相连。
十、图和矩阵的转化
邻接矩阵可简化为一个nxn的二维数组,假设数组为A[1n,.n],则数组元素Ai,i]描述了顶点i与顶
点i之间的相邻信息,即此二顶点之间的边或弧信息。在“图”中,数组元素分别使用1和0描述顶点之间是否相邻。
十一、查找算法
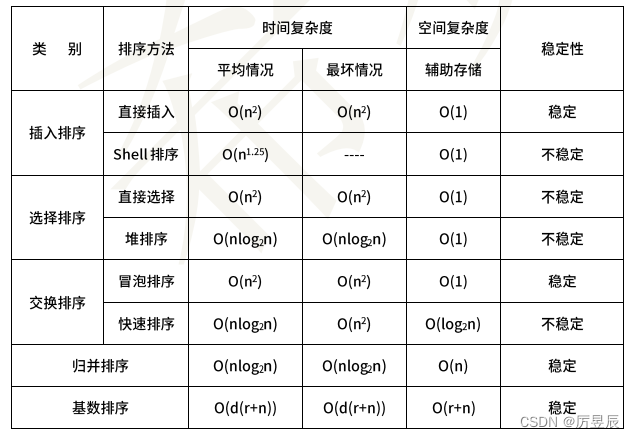
排序总表: