概要

提示：这里可以添加技术概要

       上世纪 50、60 年代，积分非线性度、差分非线性度、单调性、无失码、增益误差、 失调误差、漂移等直流性能规格主要用于表示数据转换器的性能特性。在当时，这些 规格数据就足够了，因为多数早期应用（PCM 和雷达除外）都仅涉及工业测量和过程 控制等应用中的直流或低频信号。到了 70、80 年代，随着微处理器和数字信号处 理(DSP)技术的出现，为了满足更加复杂的信号处理应用的需要，转换器需要测定信 噪比(SNR)、无杂散动态范围(SFDR)等动态性能规格。

整体架构流程

提示：这里可以添加技术整体架构

      现代的数据转换器应用覆盖从低频工业测量到宽带无线电接收器的整个频谱。虽然直 流特性的重要性随着信号频率的增加而降低，但在许多应用中仍然占有重要地位。例 如，在 IF 采样应用中，较大的增益和/或失调误差可能导致信号削波，从而降低 SNR 和 SFDR 性能。在要求匹配转换器的应用中，如交错、同步采样、I/Q 信号处理等，各转换器之间的相对增益和失调相匹配显得至关重要。 本文旨在说明数据转换器的各项直流性能特性，便于读者了解 ADC 或 DAC 数据手册 中相应部分的重要性。

技术名词解释

提示：这里可以添加技术名词解释

ADC:
      模拟数字转换器即A/D转换器，或简称ADC，通常是指一个将模拟信号转变为数字信号的电子元件。通常的模数转换器是将一个输入电压信号转换为一个输出的数字信号。由于数字信号本身不具有实际意义，仅仅表示一个相对大小。故任何一个模数转换器都需要一个参考模拟量作为转换的标准，比较常见的参考标准为最大的可转换信号大小。而输出的数字量则表示输入信号相对于参考信号的大小
 

技术细节

提示：这里可以添加技术细节

需要注意的是，对于 DAC 和 ADC 来说，要么输入要么输出为数字信号，因此其信号 具有量化性质。换言之，一个 N 位字代表了 2 N种可能状态之一，因此，一个 N 位 DAC （具有固定基准电压）只能有 2 N个可能模拟输出，一个 N 位 ADC 只能有 2 N个可能数 字输出。如前所述，模拟信号一般为电压或电流。 数据转换器的分辨率有几种不同的表述方式：最低有效位(LSB)、满量程百万分率 (ppm FS)、毫伏(mV)等。不同的器件（即使来自同一制造商）采用不同的特性规格方 式，因此，转换器用户必须了解如何在不同规格间进行转换，才能对不同器件进行有 意义的比较。各种分辨率的最低有效位大小如图所示

 显示了一个 3 位单极 DAC 和一个 3 位单极 ADC 的理想传递特性。在 DAC 中，输 入和输出都经过量化处理，其图形由 8 个点构成——虽然可以探讨这些点形成的直线， 但必须记住，实际的传递特性并非直线，而是多个离散的点

         ADC 的输入为模拟性质，未经过量化处理，但其输出却具有量化属性。因此，传递特 性由 8 个水平阶梯构成。在考虑 ADC 的失调、增益和线性度时，我们会关注这些阶梯 中点的连线——通常称为码中心。 对于 DAC 和 ADC，数字满量程（全“1”）相当于比模拟满量程(FS)低 1 个 LSB。（理 想）ADC 转换发生在比零高½LSB 时，其后，每增加 1LSB，就转换一次，直到比模拟 满量程低 1½LSB 时。由于 ADC 的模拟输入可以接受任何值，然而数字输出经量化处 理，所以，实际模拟输入与数字输出的确切值之间可能存在最高½LSB 的误差。这称 之为量化误差或量化不确定性，如图 所示。在交流（采样）应用中，这种量化误差 会导致量化噪声，其他文章对此有详细描述。

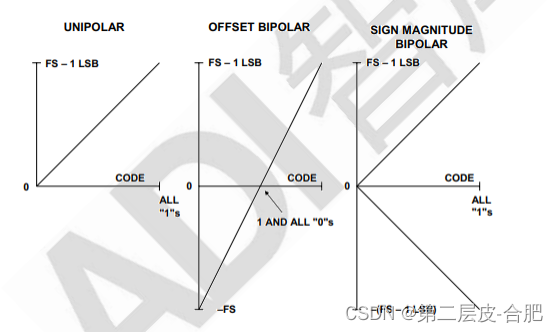
    的示例采用单极转换器，其模拟端口仅有单一极性。这属于最简单的类型，但 双极性转换器一般在现实应用中更有效。双极性转换器分为两类：较简单的一类只是 一种单极性转换器，负失调正好为 1MSB（许多转换器采用特别设计，可以根据需要 开启或关闭该失调，从而可以当作单极性或双极性转换器使用）；另一类称为符号幅 度转换器，更加复杂，具有 N 位幅度信息，另有一位相当于模拟信号的符号位。符号 幅度 DAC 非常罕见，符号幅度 ADC 主要用于数字电压表(DVM)中。单极性、偏移二进 制和符号幅度如图 所示。

      数据转换器的四项直流误差为失调误差、增益误差和两种线性度误差（差分和积分）。 失调误差和增益误差类似于放大器中的失调误差和增益误差，如图所示，图中为双 极性输入范围。（尽管失调误差和零误差在放大器和单极性数据转换器中相等，但在 双极性转换器中并不相等，必须仔细区别。

小结

提示：这里可以添加总结

       DAC 和 ADC 的传递特性可以表示为由 D=K+GA 得到的直线，其中，D 为数字码，A 为 模拟信号，K 和 G 为常数。在单极性转换器中，K 的理想值为 0；在失调双极性转换 器中，该值为–1MSB。失调误差为 K 的实际值与理想值之差。 增益误差为 G 与其理想值之差，一般表示为两者之间的百分比差，不过也可定义为满 量程下增益误差对总误差的贡献（单位：mV 或 LSB）。通常情况下，数据转换器的 用户可以调整这些误差。但请注意，放大器失调在零输入下调整，增益在近满量程下 调整。双极性数据转换器的调整算法比较复杂。