本文主要介绍粒子群算法的背景与理论,并结合对应部分的MATLAB程序对其实现流程做了阐述,代码获取方式见文末。
00 文章目录
1 粒子群优化算法
2 问题导入
3 MATLAB程序实现
4 改进策略
5 展望
01 粒子群优化算法
1.1 粒子群优化算法背景
近年来,人们通过对社会型生物群体行为的模拟提出了一类新型的生物启发式计算方法——群体智能优化算法。群体智能优化算法的核心思想主要来源于大自然的某种特殊现象或者群体动物的某种特殊行为,尤其是生物群体之间的高智能性协调合作机制,比如鸟群与鱼群的协同运动(见图2.8)、大雁群体的迁徙、蚂蚁群体的协同工作、狼群的协同扑食等。群体智能优化算法一经提出,便引起多个学科领域研究人员的广泛关注,成为人工智能以及社会、经济、生物等交叉学科的热点和前沿领域。

图源于网络,侵删
粒子群算法(particle swarm optimization,PSO)是在1995年由美国社会心理学家Kennedy和电气工程师 Eberhart 提出的[1],主要思想来源于对鸟类群体行为的研究,他们的模型和仿真算法主要利用了生物学家Heppner 提出的模型[2]。
PSO算法解决问题是先初始化一组随机解,通过迭代搜寻最优值。在PSO算法中,每个优化问题的解看做搜索空间的一只鸟,称为“粒子”。所有的粒子对应着优化问题的适应值,粒子的速度决定其飞行的方向和距离,粒子通过追寻群体中的最优粒子来完成在解空间的搜索。PSO算法自提出以来,由于其计算简单、易于实现、控制参数少等特点,引起了国内外相关领域众多学者的关注和研究。
对 PSO算法的研究主要体现在3个方面:一是对PSO算法理论的研究,二是对PSO算法的性能改进研究,三是将PSO算法应用在各个领域。从目前的研究情况来看,对后两方面的研究占了绝大多数。
1.2 标准粒子群优化算法
PSO算法的基本思想是通过群体中个体之间的协作和信息共享来寻找最优解,是一种基于群体智能的仿生智能计算方法。首先,随机初始化一群没有体积和质量的粒子,将每个粒子视为优化问题的一个可行解,粒子的好坏由一个事先设定的适应度函数来确定。每个粒子将在可行解空间中运动,并由一个速度变量决定其方向和距离。通常粒子将追随当前的最优粒子,并经过逐代搜索后得到最优解。在每一代中,粒子将跟踪两个最优解:一是粒子本身迄今为止找到的最优解;另一个是整个群体迄今为止找到的最优解。
假设一个由n个粒子组成的群体在D维的搜索空间以一定的速度飞行。粒子i状态属性设置如下:
位置(也即代表了决策变量):
其中,粒子每维的数值应在其搜索空间的上下限内,根据目标函数即可计算出每个粒子位置Xi对应的适应度值。
速度: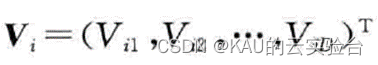
个体极值: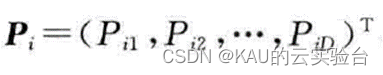
种群的群体极值:
其中,i=1,2,…,N
在每次迭代过程中,粒子通过个体极值和群体极值更新自身速度和位置,即: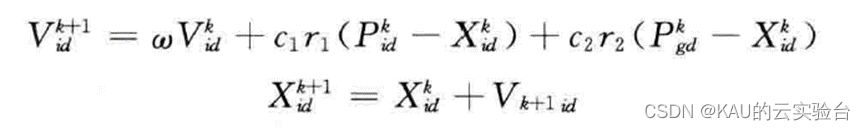
式中,w为惯性权重;d=1,2,…,D;i=1,2,…,n;k为当前迭代次数;Vid为粒子速度;r1,r2,为区间(0,1)内均匀分布的随机数;c1,c2,分别称为个体认知因子和社会学习因子(二者统称加速度因子),通常取c1=c2。为防止粒子的盲目搜索,一般建议将其位置和速度限制在一定的区间。
对于上式中的: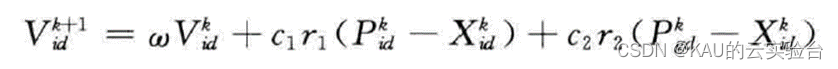
其右边由三部分组成:
第一部分为“惯性”部分﹐反映了粒子的运动“习惯”,代表粒子有维持自己先前速度的趋势;
第二部分为“认知”部分,反映了粒子对自身历史经验的记忆,代表粒子有向自身历史最佳位置逼近的趋势;
第三部分为“社会”部分,反映了粒子间协同合作与知识共享的群体历史经验,代表粒子有向群体或邻域历史最佳位置逼近的趋势。
由此看来,粒子群算法的通用性比较好,适合处理多种类型的目标函数和约束,并且容易与传统的优化方法结合,从而改进自身的局限性,更高效地解决问题。
02 问题导入
引入一个多峰的非线性函数来验证PSO算法的性能,函数如下: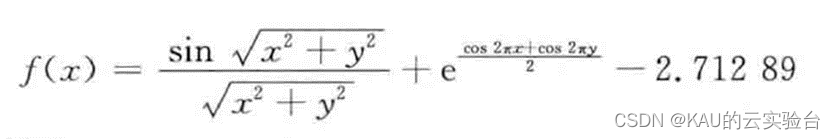
其图像如下: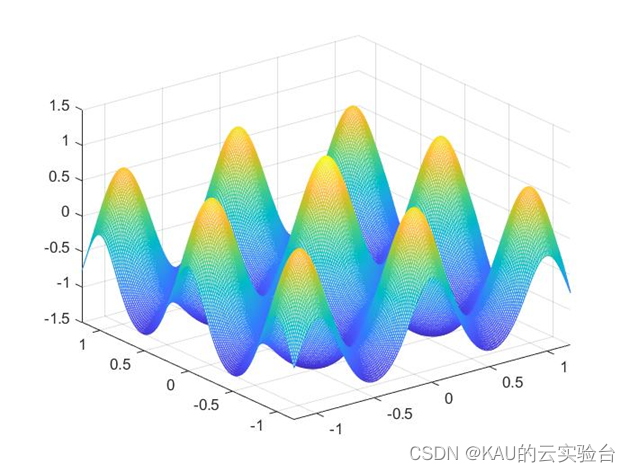
其极限位置是在(0,0)附近取得极大值,极大值为1.0054
03 MATLAB程序实现
粒子群算法的执行流程如下,按照图中的思路进行编码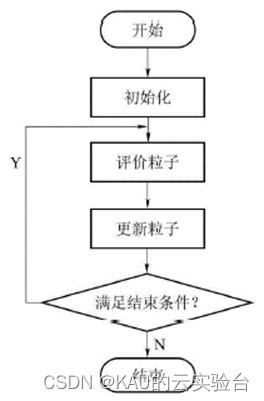
其中,本文在惯性权重部分采用线性递减的权重策略,因为Shi等[3] 指出了惯性权重的作用,即较大的惯性权重有利于全局寻优,而较小的惯性权重则有利于局部寻优。因此,如果在迭代计算过程中惯性权重呈线性递减,例如由0.9到0.4等,则 PSO 算法在开始时具有良好的全局搜索性能,能够迅速定位到接近全局最优点的区域,而在后期具有良好的局部搜索性能,能够精确得到全局最优解。线性递减公式如下: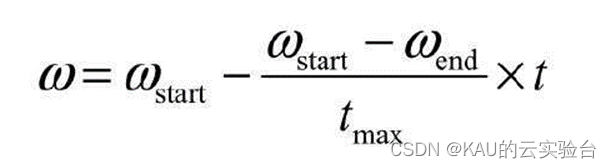
式中,tmax,为最大迭代次数;t为当前迭代次数;wstrat为初始惯性权重; wend为终止惯性权重。
3.1 初始化
初始化包括设置粒子群参数与初始化粒子位置以及速度。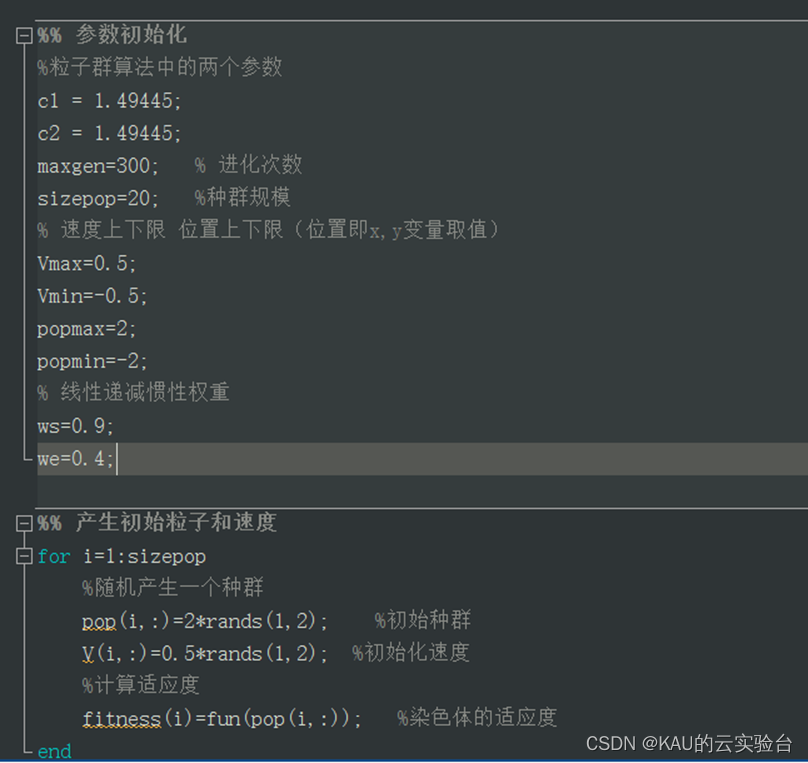
3.2 评价粒子
即寻找最优粒子与赋值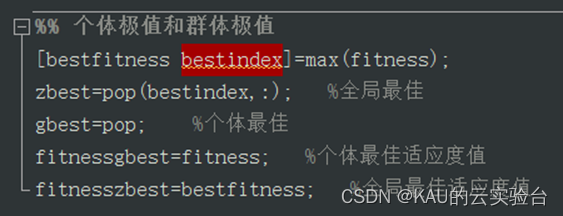
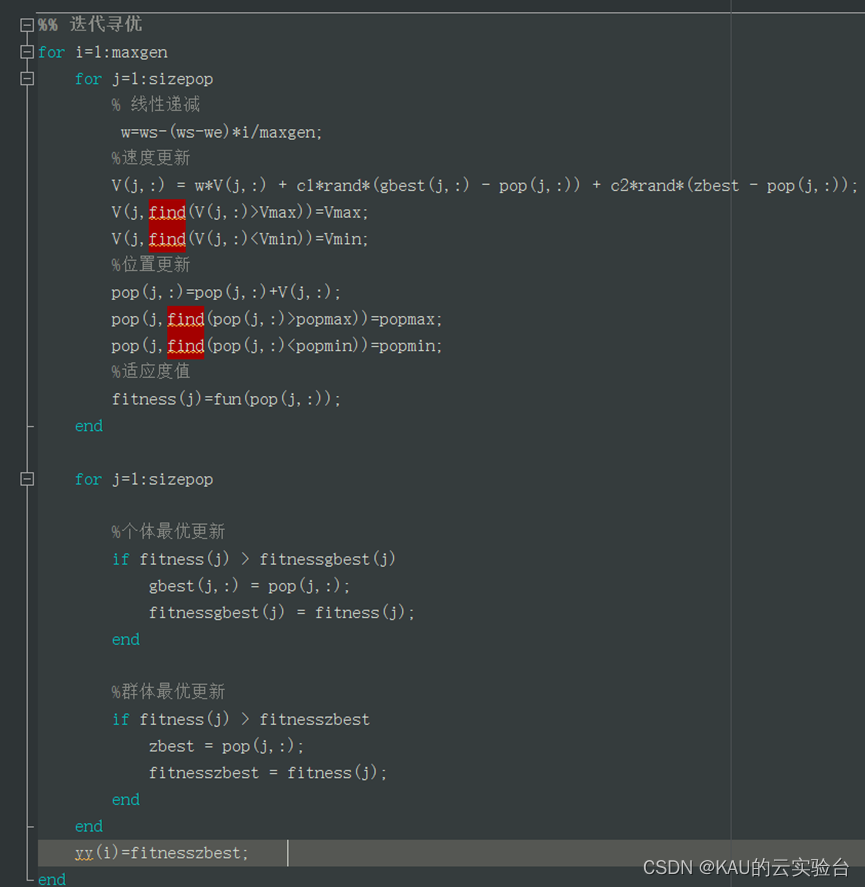
3.3 更新粒子并迭代
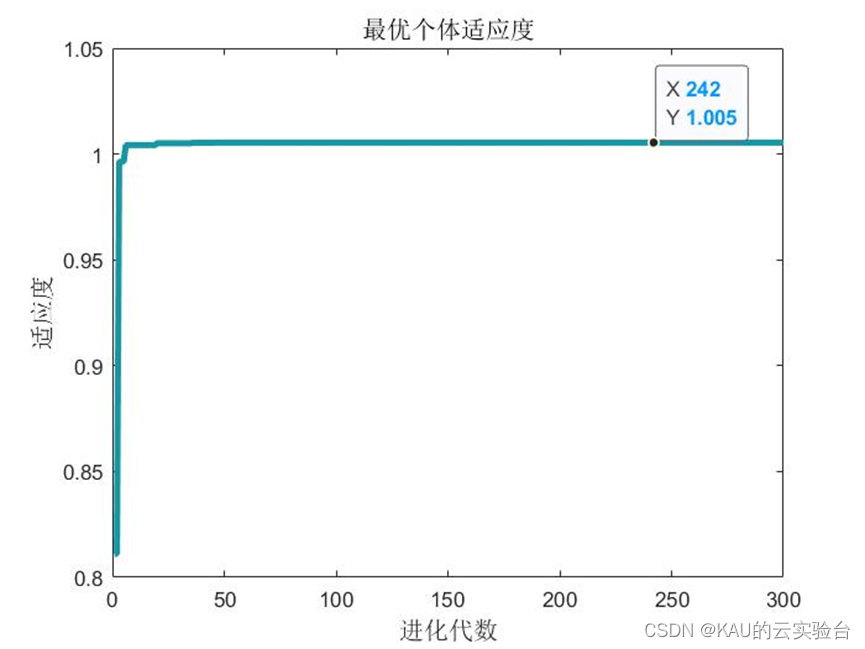
3.4 运行结果
运行出的最优适应度、最优位置为: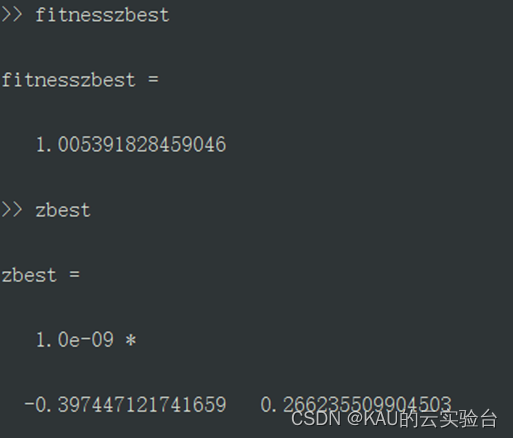
由此看出差不多取到了极限值了。
04 改进策略
Clerc于1999年在进化方程中引入压缩因子以保证算法的收敛性,同时使得速度的限制放松,使PSO算法具有更好的收敛速度;
Angeline于 1998年和1999年借鉴进化计算中的选择和杂交概念,将其引入PSO算法中以提高算法的收敛性;
Lovbjerg等人于2001年将遗传算法中的子群体概念引人PSO算法中,同时引人繁殖算子以进行子群体的信息交流宏;
窦全胜等人于2005年从增强粒子群优化能力出发,将模拟退火和分工策略两种机制引入到了PSO算法中;
刘宇等人于2006年充分利用粒子速度信息,改变了粒子速度的更新方式,并且引人了精英集团策略,提出了简约PSO算法﹔
刘洪波等人于2006年在分析了PSO算法的收敛性的基础上利用混沌特性提高群体的多样性和搜索遍历性,提高了粒子的持续搜索能力;
…
本文粒子群代码获取方式,
##########################################################
微信公众号 KAU的云实验台 回复 PSO
##########################################################
这些改进方法作者也将在后面的文章中陆续更新,如果这篇文章对你有帮助或启发,可以点赞或关注哦 (ง •̀_•́)ง(不点也行)
参考文献
[1] Ozcan E,Mohan C. Particle swarm optimization:Surfing the waves[C].Proceedings of 1999 Congresson Evolutionary Computation,1999,1939~1943.
[2] Heppner F , Grenander U. A stochastic nonlinear model for coordinated bird flocks[ M]. AAASPublications,1990.
[3] Shi Y, Eberhart R. A modified particle swarm optimizer [C]. In: Proceedings ofIEEE International Conference on Evolutionary Computation, 1998: 69-73.