文章目录
- 918. 环形子数组的最大和
- 题目解析
- 状态转移方程
- f[i]状态转移方程
- g[i]状态转移方程
- 初始化
- 返回值
- 完整代码
- 152. 乘积最大子数组
- 题目解析
- 状态转移方程
- f[i]状态转移方程
- g[i]状态转移方程
- 初始化
- 完整代码
- 1567. 乘积为正数的最长子数组长度
- 题目解析
- 状态转移方程
- f[i]状态转移方程
- g[i]状态转移方程
- 初始化
- 完整代码
918. 环形子数组的最大和
点击查看: 环形子数组的最大和
给定一个长度为 n 的环形整数数组 nums ,返回 nums 的非空 子数组 的最大可能和 。
环形数组 意味着数组的末端将会与开头相连呈环状。形式上, nums[i] 的下一个元素是 nums[(i + 1) % n] , nums[i] 的前一个元素是 nums[(i - 1 + n) % n] 。
子数组 最多只能包含固定缓冲区 nums 中的每个元素一次。形式上,对于子数组 nums[i], nums[i + 1], …, nums[j] ,不存在 i <= k1, k2 <= j 其中 k1 % n == k2 % n 。
示例 1:
输入:nums = [1,-2,3,-2]
输出:3
解释:从子数组 [3] 得到最大和 3
示例 2:
输入:nums = [5,-3,5]
输出:10
解释:从子数组 [5,5] 得到最大和 5 + 5 = 10
题目解析

可以只取3,或者取3和-2
由于数组是环形的,所以在3和-2的基础上再取1 和-2
通过比较,取3是最大和
状态转移方程
先将环形数组转化为 普通的数组 ,然后再解决
情况1:

当前数组想要取最大和,则只需取3 即可
则当前数组的最大和就在数组内部,该数组在当前情况下可看作是普通数组
可以使用 最大子数组和的解法来解决当前问题
情况2:

当前数组想要取最大和,则需取后面的5以及 环形连接的前面的5
整段数组的和为定值,若想取 当前红色区域的最大值,则需取空白区域的最小值
由于红色区域是不连续的,而空白区域为连续区间
所以可以先求 空白区域的最小子数组和
再通过整体数组和减去 空白区域的最小数组和 则为 红色区域的最大子数组和
情况1的最大子数组和 用 f 表示
情况2的最小子数组和用 g 表示

f[i]:表示以i为结尾的所有子数组中的最大和
g[i]:表示以i为结尾的所有子数组中的最小和
f[i]状态转移方程
将子数组划分为两类
1. i位置元素本身(长度为1)
该情况下:f[i]=nums[i]
2. i位置元素加上前面元素结合(长度大于1)
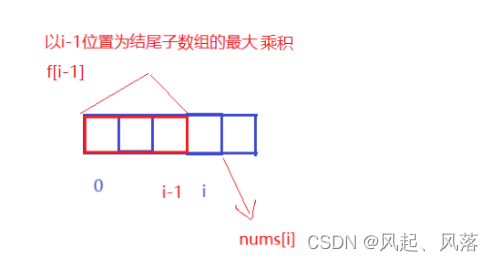
因为要求的是以i位置为结尾的子数组最大和,所以应该先求 以i-1位置为结尾的子数组的最大和 即 f[i-1]
在加上nums[i] ,就为以i位置为结尾的子数组最大和
该情况下:f[i]=f[i-1]+nums[i]
状态转移方程为:
f[i]=max(nums[i],f[i-1]+nums[i])
g[i]状态转移方程
g[i]与f[i]不同的是,f[i]要的是最大值,而g[i]要的是最小值,其他分析都是相同的
g[i]可以分为两类
情况1:i位置元素本身(长度为1)
该情况下:g[i]=nums[i]
情况2:i位置元素与前面元素结合(长度大于1)
想求以i为结尾的最小子数组和,就需要先求 以i-1为结尾的最小子数组和 即g[i-1]
在加上nums[i],就为 以i为结尾的最小子数组和
该情况下:g[i]=g[i-1]+nums[i]
状态转移方程为:
g[i]=min(nums[i],g[i-1]+nums[i])
初始化
根据状态转移方程,若i为0,则会发生越界问题

为了防止这种越界问题出现,所以加入一个虚拟节点
扩展后的数组,虚拟节点处下标为0,则 原数组的元素下标从1开始

对于f[i]状态转移方程来说,若i为1,则f[1]=max(nums[1],f[0]+nums[1])
由于下标为0处为虚拟节点,所以应使f[0]不干扰结果 ,所以将f[0]置为0

对于g[i]状态转移方程来说,若i为1,则g[1]=max(nums[1],g[0]+nums[1])
由于下标为0处为虚拟节点,所以应使g[0]不干扰结果 ,所以将g[0]置为0
返回值
对于刚开始分析的两种情况
情况1
取f表中的最大值 即 fmax
fmax即 情况1的最大子数组和
情况2
取g表中的最小值即 gmin
由于情况2的红色区域的最大子数组和 为 数组整体减去 白色区域子数组和
所以 情况2的最大子数组和 为 sum-gmin
环形数组的最大子数组和 为: max(fmax,sum-gmin)

g为一个连续的子数组,和为最小,所以gmin为当前数组的三个元素全部加上才为最小和
使用sum-gmin,则会导致 情况2的最大子数组和为0
使最终求环形数组的最大子数组和 时,预期为最大负数,结果为0,造成错误
所以要加上判断条件
若 sum==gmin (数组内元素全为负),直接返回fmax 即可
若上述判断不成立,则 返回 max(fmax,sum-gmin)
完整代码
class Solution {
public:
int maxSubarraySumCircular(vector<int>& nums) {
int n=nums.size();
//为了防止越界问题,所以多开辟一个空间
vector<int>f(n+1,0);
vector<int>g(n+1,0);
//初始化
f[0]=0;
g[0]=0;
int i=0;
//sum为整体数组和
int sum=0;
for(i=0;i<n;i++)
{
sum+=nums[i];
}
//取f表中的最大值
int fmax=INT_MIN;
//取g表中的最小值
int gmin=INT_MAX;
for(i=1;i<=n;i++)
{
//由于当前下标为扩展数组f/g的下标
//想要使用当前下标 去寻找 对应nums的值
//需要下标减1
f[i]=max(nums[i-1],f[i-1]+nums[i-1]);
g[i]=min(nums[i-1],g[i-1]+nums[i-1]);
fmax=max(fmax,f[i]);
gmin=min(gmin,g[i]);
}
//有可能存在数组元素全为负的情况,所以需要判断
return sum==gmin?fmax:max(fmax,sum-gmin);
}
};
152. 乘积最大子数组
点击查看:乘积最大子数组
给你一个整数数组 nums ,请你找出数组中乘积最大的非空连续子数组(该子数组中至少包含一个数字),并返回该子数组所对应的乘积。
测试用例的答案是一个 32-位 整数。
子数组 是数组的连续子序列。
示例 1:
输入: nums = [2,3,-2,4]
输出: 6
解释: 子数组 [2,3] 有最大乘积 6。
示例 2:
输入: nums = [-2,0,-1]
输出: 0
解释: 结果不能为 2, 因为 [-2,-1] 不是子数组。
题目解析

取2和3乘积为 子数组最大乘积
乘积变为6
若在此基础上再取 -2 ,乘一个负数就会导致 越乘越小
乘积变为 -12
状态转移方程

f[i]:表示 以i位置为结尾的 所有子数组的 最大乘积
g[i]:表示以i位置为结尾的 所有子数组的 最小乘积
f[i]状态转移方程
f[i]可以分为两类:
情况1:i位置处元素本身(长度为1)
该情况下:f[i]=nums[i]
情况2:i位置处元素与前面元素结合(长度大于1)
情况1 若nums[i]大于0
想求i位置处的最大乘积,就要先求i-1位置处的最大乘积即f[i-1]
再乘以nums[i],即 nums[i]大于0情况下,i位置处的最大乘积
即 f[i]=f[i-1]*nums[i]
情况2 若nums[i]小于0
若nums[i]为负,而f[i-1]为以i-1为结尾的最大乘积,就会造成越乘越小
所以需要在前面应乘以一个最小乘积 这样就会使两者越乘越大
即 以i-1为结尾的所有子数组的最小乘积 g[i-1]
再乘以nums[i] 即为 nums[i]小于0情况下,i位置处的最大乘积
即 f[i]=g[i-1]*nums[i]
状态转移方程为:
f[i]=max(nums[i] , max(f[i-1]*nums[i],g[i-1]*nums[i]) )
g[i]状态转移方程
情况1 i位置处元素(长度为1)
g[i]=nums[i]
情况2 i位置处元素加上前面元素结合(长度大于1)
若nums[i]大于0
想求i位置处的最小乘积,就要先求i-1位置处的最小乘积即g[i-1]
再乘以nums[i],即 nums[i]大于0情况下,i位置处的最小乘积
即 g[i]=g[i-1]*nums[i]
若nums[i]小于0
想求i位置处的最小乘积,就要先求i-1位置处的最大乘积即f[i-1]
再乘以nums[i],即 nums[i]小于0情况下,i位置处的最小乘积
即 g[i]=f[i-1]*nums[i]
状态转移方程为:
g[i]=min(nums[i] ,min(g[i-1]*nums[i],f[i-1]*nums[i]) )
初始化
若i为0时,就会发生越界问题

当i为1时
g[1]=min(nums[1] ,min(g[0]*nums[1],f[0]*nums[1]) )
为了不让f[0]或者g[0] 干扰结果,所以将 f[0]和g[0] 都置为1
完整代码
class Solution {
public:
int maxProduct(vector<int>& nums) {
int n=nums.size();
//为了防止越界问题,所以进行将数组多加一个虚拟节点
vector<int>f(n+1,0);
vector<int>g(n+1,0);
//初始化
f[0]=1;
g[0]=1;
int i=0;
int ret=INT_MIN;
for(i=1;i<=n;i++)
{
//当前下标为扩展数组f/g的下标
//想要使用当前下标 去寻找对应的原数组的值
//需要将下标减1
f[i]=max(nums[i-1],max(f[i-1]*nums[i-1],g[i-1]*nums[i-1]));
g[i]=min(nums[i-1],min(g[i-1]*nums[i-1],f[i-1]*nums[i-1]));
ret=max(ret,f[i]);
}
return ret;
}
};
因为返回值为 最大乘积 ,所以只需返回f表中最大值即可
1567. 乘积为正数的最长子数组长度
点击查看:乘积为正数的最长子数组长度
给你一个整数数组 nums ,请你求出乘积为正数的最长子数组的长度。
一个数组的子数组是由原数组中零个或者更多个连续数字组成的数组。
请你返回乘积为正数的最长子数组长度。
示例 1:
输入:nums = [1,-2,-3,4]
输出:4
解释:数组本身乘积就是正数,值为 24 。
示例 2:
输入:nums = [0,1,-2,-3,-4]
输出:3
解释:最长乘积为正数的子数组为 [1,-2,-3] ,乘积为 6 。
注意,我们不能把 0 也包括到子数组中,因为这样乘积为 0 ,不是正数。
题目解析
子数组必须为连续的,子数组的乘积为正,找到所有乘积为正的子数组中 长度 最长的哪一个

选择乘积 1 -2 -3,乘积为正数,长度为 3
选择乘积 -2 -3 4,乘积为正数,长度为 3
选择乘积 1 -2 -3 4,乘积为正数,长度为 4
所以最长 长度为4
状态转移方程
f[i]:表示以i位置为结尾的 所有子数组中 乘积为正数的 最长长度
g[i]:表示以i位置为结尾的 所有子数组中 乘积为负数的 最长长度
f[i]状态转移方程
情况1 i位置处元素本身 (长度为1)

若num[i]大于0,则f[i]为1
若nums[i]小于0,则f[i]为0
情况2 i位置元素 加上前面元素结合(长度大于1)
若nums[i[大于0,则前面需乘以乘积为正数的最长长度

想求以i位置为结尾的 所有子数组中 乘积为正数的 最长长度,因为nums[i]大于0,则需先求以i-1位置结尾的 所有子数组中 乘积为正数的 最长长度即 f[i-1]
在加上后面i位置处的长度 即+1
该情况下: f[i]=f[i-1]+1
若nums[i]小于0 ,则前面需乘以乘积为负数的最长长度
这样才可以保证整体 乘积为正数

想求以i位置为结尾的 所有子数组中 乘积为正数的 最长长度,因为nums[i]小于0,则需先求以i-1位置结尾的 所有子数组中 乘积为负数的 最长长度即 g[i-1]
在加上后面i位置处的长度 即+1
如果直接写成 f[i]=g[i-1]+1
若数组中以i-1为结尾的乘积全都大于0,i位置处小于0,则没办法生成乘积为正数的长度,预期结果为0,f[i]值为1,造成结果错误
所以需先判断 g[i-1]是否等于0(若等于0说明以i-1为结尾的乘积全都大于0)
若g[i-1]等于0,则f[i]=0
若g[i-1]不等于0,则f[i]=g[i-1]+1
即 f[i] =g[i-1]==0?0:g[i-1]+1
状态转移方程为:
if(nums[i]>0)
f[i]=f[i-1]+1
if(nums[i]<0)
f[i]=g[i-1]==0?0:g[i-1]+1
g[i]状态转移方程
情况1 长度为1

g[i]表示以i结尾的所有子数组中 乘积为负的最长长度
若nums[i]大于0,则g[i]为0
若num[i]小于0,则g[i]为1
情况2 长度大于1
若nums[i]大于0 ,则前面需乘以 乘积为负的最长长度
使整体数组 乘积 为负

想求以i位置为结尾的 所有子数组中 乘积为负数的 最长长度,因为nums[i]大于0,则需先求以i-1位置结尾的 所有子数组中 乘积为负数的 最长长度即 g[i-1]
在加上后面i位置处的长度 即+1
如果直接写成 g[i]=g[i-1]+1
若数组中以i-1为结尾的乘积全都大于0,i位置处大于0,则没办法生成乘积为负数的长度,预期结果为0,f[i]值为1,造成结果错误
所以需先判断 g[i-1]是否等于0(若等于0说明以i-1为结尾的乘积全都大于0)
若g[i-1]等于0,则g[i]=0
若g[i-1]不等于0,则g[i]=g[i-1]+1
即 g[i] =g[i-1]==0?0:g[i-1]+1
若nums[i]小于0,则前面需乘以乘积为正的最长 长度
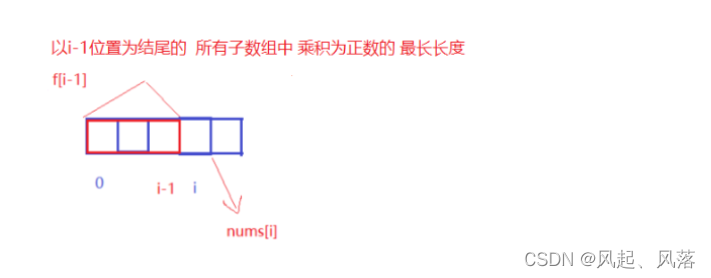
想求以i位置为结尾的 所有子数组中 乘积为负数的 最长长度,因为nums[i]小于0,则需先求以i-1位置结尾的 所有子数组中 乘积为正数的 最长长度即 f[i-1]
在加上后面i位置处的长度 即+1
该情况下: g[i]=f[i-1]+1
状态转移方程为:
if(nums[i]>0)
g[i]=g[i-1]==0?0:g[i-1]+1
if(nums[i]<0)
g[i]=f[i-1]+1
初始化
若i为0时,就会发生越界问题

当nums[i]小于0时,若i为1,则g[1]=f[0]+1
为了不让f[0]干扰结果,所以将f[0]=0
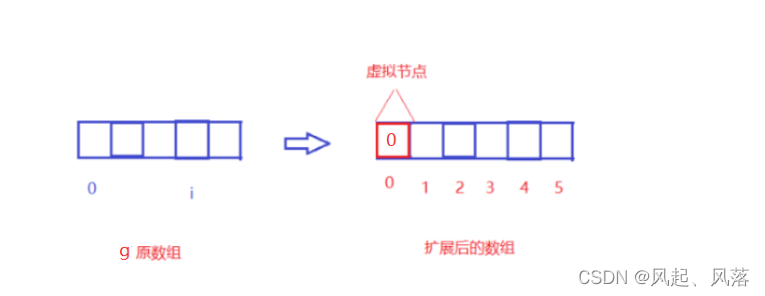
由于当前使用下标为f/g扩展数组的下标
所以想要使用当前下标 ,寻找到对应nums的值
需要下标减1
所以当i为1时,取nums[0]值,若nums[0]>0,则g[0]==0
(g[0]表示以下标0为结尾的所有子数组的乘积负数的最长长度)
nums[0]大于0,说明没有乘积为负的情况,所以g[0]取0
完整代码
class Solution {
public:
int getMaxLen(vector<int>& nums) {
int n=nums.size();
//为了避免越界问题,所以设置一个虚拟节点
vector<int>f(n+1,0);
vector<int>g(n+1,0);
//初始化
f[0]=0;
g[0]=0;
int i=0;
int ret=INT_MIN;
for(i=1;i<=n;i++)
{
//由于当前使用下标为f/g扩展数组的下标
//所以想要使用当前下标 ,寻找到对应nums的值
//需要下标减1
if(nums[i-1]>0)
{
f[i]=f[i-1]+1;
g[i]=g[i-1]==0?0:g[i-1]+1;
}
else if(nums[i-1]<0)
{
f[i]=g[i-1]==0?0:g[i-1]+1;
g[i]=f[i-1]+1;
}
ret=max(ret,f[i]);
}
//返回 f表中的最大值
return ret;
}
};
因为f表 表示乘积为正的子数组的最长长度,所以返回f表的最大值