动态规划中级阶段
- 前言
- 一、三角形最小路径和
- 1.1、思路
- 1.2、代码实现
- 二、买卖股票的最佳时机 II
- 2.1、思路
- 2.2、代码实现
- 总结
前言
动态规划(Dynamic Programming,简称 DP)是一种解决多阶段决策过程最优化问题的方法。它是一种将复杂问题分解成重叠子问题的策略,通过维护每个子问题的最优解来推导出问题的最优解。
动态规划的主要思想是利用已求解的子问题的最优解来推导出更大问题的最优解,从而避免了重复计算。因此,动态规划通常采用自底向上的方式进行求解,先求解出小规模的问题,然后逐步推导出更大规模的问题,直到求解出整个问题的最优解。
动态规划通常包括以下几个基本步骤:
- 定义状态:将问题划分为若干个子问题,并定义状态表示子问题的解;
- 定义状态转移方程:根据子问题之间的关系,设计状态转移方程,即如何从已知状态推导出未知状态的计算过程;
- 确定初始状态:定义最小的子问题的解;
- 自底向上求解:按照状态转移方程,计算出所有状态的最优解;
- 根据最优解构造问题的解。
动态规划可以解决许多实际问题,例如最短路径问题、背包问题、最长公共子序列问题、编辑距离问题等。同时,动态规划也是许多其他算法的核心思想,例如分治算法、贪心算法等。
动态规划是一种解决多阶段决策过程最优化问题的方法,它将复杂问题分解成重叠子问题,通过维护每个子问题的最优解来推导出问题的最优解。动态规划包括定义状态、设计状态转移方程、确定初始状态、自底向上求解和构造问题解等步骤。动态规划可以解决许多实际问题,也是其他算法的核心思想之一。
一、三角形最小路径和
给定一个三角形 triangle ,找出自顶向下的最小路径和。
每一步只能移动到下一行中相邻的结点上。相邻的结点 在这里指的是 下标 与 上一层结点下标 相同或者等于 上一层结点下标 + 1 的两个结点。也就是说,如果正位于当前行的下标 i ,那么下一步可以移动到下一行的下标 i 或 i + 1 。
示例 1:
输入:triangle = [[2],[3,4],[6,5,7],[4,1,8,3]]
输出:11
解释:如下面简图所示:
2
3 4
6 5 7
4 1 8 3
自顶向下的最小路径和为 11(即,2 + 3 + 5 + 1 = 11)。
示例 2:
输入:triangle = [[-10]]
输出:-10
来源:力扣(LeetCode)。
1.1、思路
定义二维 dp 数组,将解法二中「自顶向下的递归」改为「自底向上的递推」。
1、状态定义:dp[i][j] 表示从点 (i,j) 到底边的最小路径和。
2、状态转移:dp[i][j]=min(dp[i+1][j],dp[i+1][j+1])+triangle[i][j] 。
1.2、代码实现
class Solution {
public int minimumTotal(List<List<Integer>> triangle) {
int n = triangle.size();
// dp[i][j] 表示从点 (i, j) 到底边的最小路径和。
int[][] dp = new int[n + 1][n + 1];
// 从三角形的最后一行开始递推。
for (int i = n - 1; i >= 0; i--) {
for (int j = 0; j <= i; j++) {
dp[i][j] = Math.min(dp[i + 1][j], dp[i + 1][j + 1]) + triangle.get(i).get(j);
}
}
return dp[0][0];
}
}
时间复杂度:
O
(
N
2
)
O(N^2)
O(N2),N 为三角形的行数。
空间复杂度:
O
(
N
2
)
O(N^2)
O(N2),N 为三角形的行数。
二、买卖股票的最佳时机 II
给你一个整数数组 prices ,其中 prices[i] 表示某支股票第 i 天的价格。
在每一天,你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买,然后在 同一天 出售。
返回 你能获得的 最大 利润 。
示例 1:
输入:prices = [7,1,5,3,6,4]
输出:7
解释:在第 2 天(股票价格 = 1)的时候买入,在第 3 天(股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4 。
随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出, 这笔交易所能获得利润 = 6 - 3 = 3 。
总利润为 4 + 3 = 7 。
示例 2:
输入:prices = [1,2,3,4,5]
输出:4
解释:在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4 。
总利润为 4 。
示例 3:
输入:prices = [7,6,4,3,1]
输出:0
解释:在这种情况下, 交易无法获得正利润,所以不参与交易可以获得最大利润,最大利润为 0 。
来源:力扣(LeetCode)。
2.1、思路
(1)第 1 步:定义状态。
状态 dp[i][j] 定义如下:
dp[i][j] 表示到下标为 i 的这一天,持股状态为 j 时,我们手上拥有的最大现金数。
注意:限定持股状态为 j 是为了方便推导状态转移方程,这样的做法满足 无后效性。
其中:
- 第一维 i 表示下标为 i 的那一天( 具有前缀性质,即考虑了之前天数的交易 );
- 第二维 j 表示下标为 i 的那一天是持有股票,还是持有现金。这里 0 表示持有现金(cash),1 表示持有股票(stock)。
(2)第 2 步:思考状态转移方程
状态从持有现金(cash)开始,到最后一天我们关心的状态依然是持有现金(cash);
每一天状态可以转移,也可以不动。状态转移用下图表示:

说明:
- 由于不限制交易次数,除了最后一天,每一天的状态可能不变化,也可能转移;
- 写代码的时候,可以不用对最后一天单独处理,输出最后一天,状态为 0 的时候的值即可。
(3)第 3 步:确定初始值
起始的时候:
- 如果什么都不做,dp[0][0] = 0;
- 如果持有股票,当前拥有的现金数是当天股价的相反数,即 dp[0][1] = -prices[i];
(4)第 4 步:确定输出值;终止的时候,上面也分析了,输出 dp[len - 1][0],因为一定有 dp[len - 1][0] > dp[len - 1][1]。
2.2、代码实现
class Solution {
public:
int maxProfit(vector<int>& prices) {
int n = prices.size();
int dp[n][2];
dp[0][0] = 0, dp[0][1] = -prices[0];
for (int i = 1; i < n; ++i) {
dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
}
return dp[n - 1][0];
}
};
时间复杂度:O(N),这里 N 表示股价数组的长度;
空间复杂度:O(N),虽然是二维数组,但是第二维是常数,与问题规模无关。
优化:
class Solution {
public:
int maxProfit(vector<int>& prices) {
int n = prices.size();
int dp0 = 0, dp1 = -prices[0];
for (int i = 1; i < n; ++i) {
int newDp0 = max(dp0, dp1 + prices[i]);
int newDp1 = max(dp1, dp0 - prices[i]);
dp0 = newDp0;
dp1 = newDp1;
}
return dp0;
}
};
时间复杂度:O(N),这里 N 表示股价数组的长度;
空间复杂度:O(1)。
总结
动态规划(Dynamic Programming)是一种解决多阶段决策最优化问题的方法,它将复杂问题分解成重叠子问题并通过维护每个子问题的最优解来推导出问题的最优解。动态规划可以解决许多实际问题,例如最短路径问题、背包问题、最长公共子序列问题、编辑距离问题等。
动态规划的基本思想是利用已求解的子问题的最优解来推导出更大问题的最优解,从而避免了重复计算。它通常采用自底向上的方式进行求解,先求解出小规模的问题,然后逐步推导出更大规模的问题,直到求解出整个问题的最优解。
动态规划通常包括以下几个基本步骤:
- 定义状态:将问题划分为若干个子问题,并定义状态表示子问题的解;
- 定义状态转移方程:根据子问题之间的关系,设计状态转移方程,即如何从已知状态推导出未知状态的计算过程;
- 确定初始状态:定义最小的子问题的解;
- 自底向上求解:按照状态转移方程,计算出所有状态的最优解;
- 根据最优解构造问题的解。
动态规划的时间复杂度通常为 O ( n 2 ) O(n^2) O(n2)或 O ( n 3 ) O(n^3) O(n3),空间复杂度为O(n),其中n表示问题规模。在实际应用中,为了减少空间复杂度,通常可以使用滚动数组等技巧来优化动态规划算法。


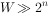

![[洛谷]P1162 填涂颜色(搜索连通块)](https://img-blog.csdnimg.cn/ba2ed2f2d4ae43e78043ae96f4f58bf6.png)