【问题描述】

题目6：数阵问题

        每个局面是三行三列的数字方阵，每个位置为0-8的一个数码且互不相同，求从初始局面（自己设定）如何“最快”移动到终止局面（自己设定）。

移动规则：每次只能0与其上下左右四个方向相邻的某个数字交换！可能有解，可能无解。

0	1	2		?		1	2	3
3	4	5		=》		4	5	6
6	7	8				7	8	0

 

【需求分析】

一、基本功能

1.用户自己设定初始界面、终止界面，九宫格上方块可移动；

2.根据初始界面和终止界面，打印出移动的路径。

 

二、附加功能

1.用户移动九宫格的回退功能；

2. 使用了A*搜索、全局择先、宽度优先三种算法，对移动路径进行搜索；

3. 针对A*搜索和全局择先算法，设计了四种估值函数；

4. 判断在指定估值函数、指定算法的情况下，移动的步数及时间，将结果存储至数据库，并在前端回显。

 

【概要设计】

一、系统信息

开发的硬件环境

        CPU：11th Gen Intel(R) Core(TM) i7-11800H @ 2.30GHz    2.30 GHz

        RAM：16.0 GB

开发该系统的操作系统

        版本：Windows 10 家庭中文版

软件开发环境/开发工具

        Intellij IDEA2021.1.1

        Visual Studio Code

        HBuilder X

         Postman、ApiPost7

编程语言

        Java

技术点

        后端技术：Springboot、SpringMVC、knife4j、Mybatis-plus、MySQL、maven、lombok

        前端技术：HTML、CSS、JavaScript、Vue、JQuery、Element-ui、Layui、axios

 

二、功能模块

        根据需求，设计的八数码求解系统的功能有，九宫格的移动、搜索移动路径、状态记录这三大类。详情如图 1所示：

 

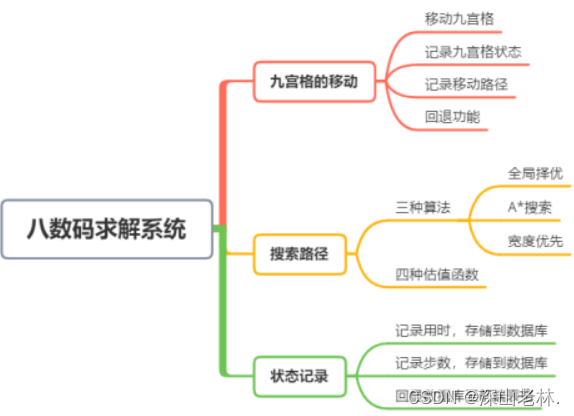
图 1 系统功能图

 

三、项目架构

（一）MVC三层架构

表 1 MVC架构表

层次	作用	设计原则
模型层（MODEL）	封装应用的一系列数据，并定义操作，处理这些数据的逻辑和计算规则	通过调用接口对控制器进行反馈
视图层 （VIEW）	视图对象的主要目的之一是将应用模型对象中的数据显示出来，并允许用户编辑该数据	通过ajax发送异步请求，和控制器进行反馈
控制器层（CONTROLLER）	控制器是在视图层和若干个模型层的中间人	直接操作模型层和视图层

 

（二）包结构

        项目使用的是基本的MVC三层架构，其中common包下存放通用实体类，config下是对tomcat服务器的配置信息，controller包下是控制层，mapper层下是数据库操作的Interface接口，service是业务层，system下是实体类，vo包下定义的类是值对象，用来传递数据和信息。包目录结构如图 2所示。

 

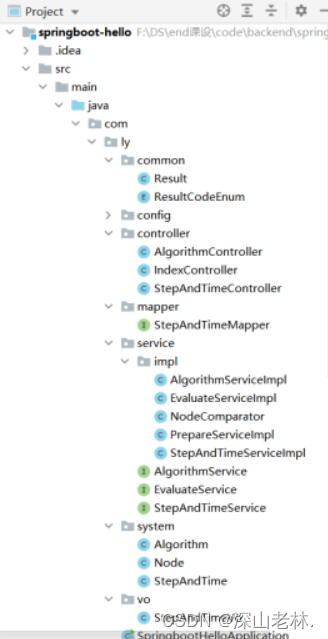
图 2 项目包目录

 

四、存储结构

        在JavaEE开发设计的过程中，和C语言的结构体类似，Java中的存储放在一个实体类中。比如跟三种算法相关的信息，我存放在了Node节点和Algorithm节点中，节点Node的存储结构如图 9所示

表 2 节点Node的存储结构

数据项名称	数据项系统表示	数据类型	数据长度	备注
存放顶点数据	num	int[][]	3*3
移动步数/深度	depth	int
逆序数	Reverse_order_number	int
父节点移动方向	direction	int
估值函数值	worth	int

        Node类的代码如下：

public class Node {



public int[][] num =new int [3][3]; //用于存放节点数据



public int depth; //移动步数/深度



int Reverse_order_number; //逆序数



public int direction;//1 2 3 4 分别为上下左右



public int worth; //启发式函数的值

}

        节点Algorithm的存储结构如表 3所示：

表 3 Algorithm的存储结构

数据项名称	数据项系统表示	数据类型	数据长度	备注
num的初始状态	num_Initial	int[][]	3*3
num的结束状态	num_Eventual	int[][]	3*3
开始时间	starTime	long
最大搜索长度	MAX_SEARCH_DEPTH	int

        类Algorithm的源码如下所示：

public class Algorithm {



    public static int[][] num_Initial =new int [3][3];



    public static int[][] num_Eventual =new int [3][3];



    public static long starTime;



    public static int MAX_SEARCH_DEPTH=100;

}

        函数执行结果的存储类为StepAndTime，存储结构如下：

表 4 StepAndTime存储结构

数据项名称	数据项系统表示	数据类型	数据长度	备注
主键	id	String
算法名	algorithm_name	String
估值函数	algorithm_value_estimate	String
时间花费	time_cost	String
步数	step	int

        StepAndTime类的代码如下：

public class StepAndTime {



    private String id;



    private String algorithm_name;



    private String algorithm_value_estimate;



    private String time_cost;



    private int step;

}

        这里的StepAndTime节点存放至了数据库，可实现数据库的增删改查的功能，其中表step_and_time的结构如图 3所示。

 

 图 3 数据库存储

 

【详细设计】

一、九宫格的移动

（一）移动九宫格

        在前端界面中放置了两个九宫格，每个九宫格里都是1-8的八个数，第一个九宫格代表初始状态，第二个九宫格代表的是目标状态，用户点击空块，即九宫格除8个有数字的块以外的块时，该块会和空块做交换，交换逻辑如图 4所示。

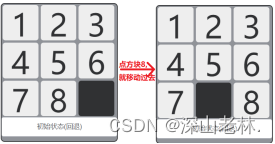
图 4 点击方块的移动效果

（二）记录九宫格状态、移动状态

        用一个ti2数组对九宫格状态进行记录，用字符串拼接的方式对九宫格移动的状态进行记录(用于回退)，将内容打印在控制台中。

 

 

图 5 记录九宫格状态

（三）回退功能

        点击下面的回退按钮，会返回前一个九宫格状态。

 

二、搜索路径

（一）全局择优算法

         全局择优搜索属于启发式搜索，即利用已知问题中的启发式信息指导问题求解，而非蛮力穷举的盲目搜索。

启发式信息：即，可用于指导搜索过程，且与具体问题求解有关的控制性信息。

启发函数：用于描述启发式信息的数学模型，称为启发函数，根据问题特点和看待问题的角度不同，同一问题，可以定义多个启发函数。

 

        全局择优算法的执行流程是先把初始节点S0放入OPEN表中，根据当前结点的深度和当前结点和目标结点差异的度量，计算出启发函数f(S0),如果OPEN表为空，那么问题没有解，直接退出程序，如果OPEN表还不为空，那就把OPNE表的第一个节点n放入CLOSED表，考察该节点是否是目标结点，如果是的，那就可以直接得出问题解，从而退出程序，如果还没找到目标节点，则节点n不可以扩展，转到Step2,如果节点n可以扩展，则扩展该节点，用估值函数f(n)计算每个节点的估价值，并给每个子结点配置指向父结点的指针，把这些子节点都放入OPEN表中，然后对OPEN表中的所有节点按照估值函数f(n)的大小进行排序，再转到Step2去，全局择优算法的执行流程如表 5所示。

表 5 全局择优算法执行流程

步骤	全局择优算法流程
Step1	把初始节点SO放入OPEN表，f(S0)
Step2	如果OPEN表为空，则问题无解，退出
Step3	把OPEN表的第一个节点(记为节点n)取出放入CLOSED表
Step4	考察节点n是否为目标节点。若是，则求得问题的解，退出
Step5	若节点n不可扩展，则转Step2
Step6	扩展节点n，用启发函数f(x)计算每个子节点的估价值，并为每个子节点配置指向父节点的指针，把这些子节点都送入OPEN表中，然后对OPEN表中的全部节点按估价值从小到大的顺序进行排序，然后转Step2

（二）A*搜索算法

        A*搜索算法相对于全局择优算法改动非常小，只增加了个别函数，全局择优、A算法和A*算法的定义、区别介绍如表 6所示：

表 6  A算法、A*算法定义

定义	全局择优算法流程
定义1	在GRAPHSEARCH过程中，如果重排OPEN表是依据f(x)=g(x)+h(x)进行的，则称该过程为A算法
定义2	在A算法中，如果对所有的x，h(x)<=h*(x）成立,则称h(x)为h*(x)的下界，它表示某种偏于保守的估计
定义3	采用h(x)的下界h*(x)为启发函数的A算法称为A*算法

        A*算法是在A算法的基础上，每生成一个新节点，即查找closed表，如果closed表中有相同排列的结点，那么则比较他们的权重(f(n))，如果新节点的权重更小，则替代原结点，即，刷新原结点的深度，这样就很有可能找到更短、更快的到达目标结点的路径。A*算法执行的流程图如图 6所示

 

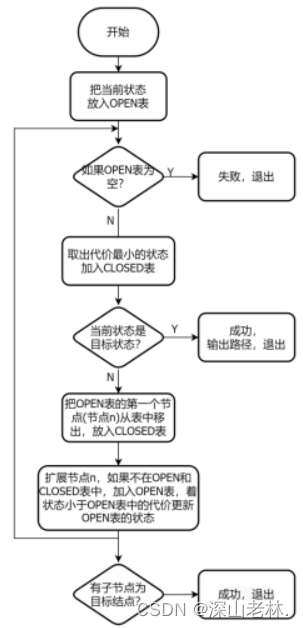
图 6 A*算法执行流程图

（三）宽度优先算法

        宽度优先算法是一种盲目搜索算法，即，蛮力法；需要一个Open表，把起始节点放入Open表中，如果Open表为空，则无解并退出，否则，继续把第一个节点n从Open表中移除，并放入CLOSED扩展节点表中。这里要考察节点n是不是目标节点，如果是的话，就代表求出答案了，则可以退出，如果节点n往下不可以接着扩展了，那么转到第二步，继续从OPEN表中选节点，放入CLOSED表考察。如果节点n可扩展，则把所有n的子节点放入OPEN表的尾部，配置父节点指针，继续转Step2开始下一轮判断。算法流程如表 7所示。

表 7 宽度优先算法流程表

步骤	宽度优先算法流程
Step1	把起始节点放到OPEN表中
Step2	如果OPEN是个空表，则没有解失败退出;否则继续
Step3	把第一个节点 (节点n) 从OPEN表移出，并把它放入CLOSED扩展节点表中
Step4	考察节点n是否为目标节点。如果是，则求得了问题的解，退出
Step5	如果节点n不可扩展，则转Step2
Step6	把n的所有子节点放到OPEN表的尾部，并为其配置指向父节点的指针然后转第Step2步

 

算法流程图如图 7所示

 

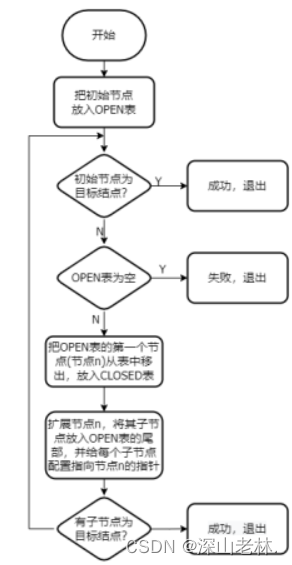
图 7 宽度优先算法流程图

 

（四）四种估值函数

        对于全局择优和A*搜索这两种算法，为了求取最优解，可以设置不同的估值函数，测试看不同的效果。这里选择了四种估值函数，估值函数的解释如图 8所示。

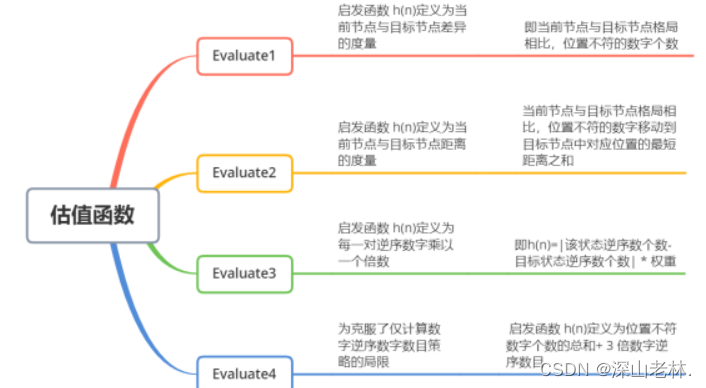
图 8 四种估值函数

 

        这里的Evaluate1和Evaluate2的启发函数定义为当前结点与目标结点差异的度量，这里的“差异”，可以是当前节点与目标节点相比，位置不符的数字个数，也可以是当前节点和目标节点格局相比，位置不符的数字移动到目标节点中对应位置的最短距离之和。

        Evaluate3定义为每一对逆序数字乘以一个倍数，即该状态下 逆序数个数与目标状态逆序数个数的绝对值乘以权重。

        Evaluate4是为了克服仅在计算数字逆序数字量策略的局限，启发函数定义为位置不符数字个数的总和+3倍逆序数字序列。

 

三、状态记录

前端使用了el-table表格，对八数码路径查找执行时的用时、步数等进行了数据的持久化存储，并利用axios调用后端接口，实现了数据的回显。在前端显示的表格中，部分数据如图 9所示。

 

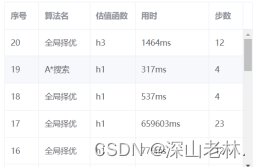
图 9 数据记录表的部分数据

【编码实现】

        由于主要功能的实现是通过估值函数类&&算法类实现的，所以在这里，仅对四种估值函数和三种算法做介绍。

一、估值函数

（一）估值函数1

        启发函数 h(n)定义为当前节点与目标节点差异的度量：即当前节点与目标节点格局相比，位置不符的数字个数。其中，估值函数Evaluate1的代码如下：

    public int Evaluate1(int a[][],int[][] num_Finish) {

        int n = 0;

        for (int i = 0; i < 3; ++i) {

            for (int j = 0; j < 3; ++j) {

                if (a[i][j] != num_Finish[i][j])

                    ++n;//找两个状态有多少个格子位置错了

            }

        }

        return n;

    }

（二）估值函数2

        启发函数 h(n)定义为当前节点与目标节点距离的度量：当前节点与目标节点格局相比，位置不符的数字移动到目标节点中对应位置的最短距离之和。其中估值函数Evaluate2如下：

public int Evaluate2(int a[][],int[][] num_Finish) {

        int h = 0;// 代价

        //找到这个数在初始状态和目标状态的位置在哪

        for (int i = 0; i < 9; ++i) {

            int m, n;

            for (m = 0; m < 9; ++m)

//二维数组遍历找0-8中的数字i，找到就往下

                if (a[m / 3][m % 3] == i) break;

            for (n = 0; n < 9; ++n)

                if (num_Finish[n / 3][n % 3] == i)//找到就往下

                    break;

            //行序差+列序差

            h += Math.abs((m / 3) - (n / 3)) + Math.abs((m % 3) - (n % 3));

        }

        return h;

    }

 

（三）估值函数3

        启发函数 h(n)定义为每一对逆序数字乘以一个倍数，即h(n)=|该状态逆序数个数-目标状态逆序数个数| * 权重

public int Evaluate3(int a[][],int[][] num_Finish) {

int weight=Math.abs(ReverseNumber(a)-ReverseNumber(num_Finish));

return weight*Math.abs(ReverseNumber(a)-ReverseNumber(num_Finish));

}

 

（四）估值函数4

        为克服了仅计算数字逆序数字数目策略的局限 启发函数 h(n)定义为位置不符数字个数的总和+ 3 倍数字逆序数目。

public int Evaluate4(int a[][],int[][] num_Finish) {

return Evaluate1(a,num_Finish) + 3 * Math.abs(ReverseNumber(a) - ReverseNumber(num_Finish));

}

 

二、搜索算法

（一）全局择先算法

        全局择优算法的执行流程是先把初始节点S0放入OPEN表中，根据当前结点的深度和当前结点和目标结点差异的度量，计算出启发函数f(S0),如果OPEN表为空，那么问题没有解，直接退出程序，如果OPEN表还不为空，那就把OPNE表的第一个节点n放入CLOSED表，考察该节点是否是目标结点，如果是的，那就可以直接得出问题解，从而退出程序，如果还没找到目标节点，则节点n不可以扩展，转到Step2,如果节点n可以扩展，则扩展该节点，用估值函数f(n)计算每个节点的估价值，并给每个子结点配置指向父结点的指针，把这些子节点都放入OPEN表中，然后对OPEN表中的所有节点按照估值函数f(n)的大小进行排序，再转到Step2去，全局择优算法的执行流程如表 5所示。其中，全局择先函数如下：

public int[][][]  GlobalSearch2(long info[],int nEvaluate,int[][] num_Begin,int[][] num_Finish) {



        starTime = System.nanoTime();



        Vector<Node> OPEN=new Vector<Node>();

        Vector<Node> CLOSED=new Vector<Node>();



        // 添加根节点

        OPEN.add(new Node(num_Begin, 0, evaluateService.ReverseNumber(num_Begin), 0, null, evaluateService.Evaluate(num_Begin, 0, nEvaluate,num_Finish)));



        while(!OPEN.isEmpty()) {



            // 计算可达性,限制搜索深度

            if (!isAvailable(OPEN.get(0).num,num_Finish) || OPEN.get(0).depth > MAX_SEARCH_DEPTH) {

                return null;

            }



            CLOSED.add(OPEN.get(0));

            OPEN.remove(0);



            if(isEqual(CLOSED.lastElement().num,num_Finish)) {



                return Route2(CLOSED.lastElement(),info);

            }

            else {



                Node father=CLOSED.lastElement();

                int i = 0, j = 0;



                // 找到空格

                for (int k = 0; k < 9; ++k) {

                    if (father.num[k / 3][k % 3] == 0) {

                        i = k / 3;

                        j = k % 3;

                        break;

                    }

                }



                int dir=father.direction,dep=father.depth;

                int a[][]=new int[3][3];



                //1 上

                if (i != 0&& dir!=2) {



                    for (int m = 0; m < 3; ++m) {

                        for (int n = 0; n < 3; ++n) {

                            a[m][n]=father.num[m][n];

                        }

                    }



                    a[i][j]=a[i-1][j];

                    a[i-1][j]=0;



                    OPEN.add(new Node(a, dep + 1, evaluateService.ReverseNumber(a), 1, father,evaluateService.Evaluate(a, dep + 1, nEvaluate,num_Finish)));



                }

              //参照“1 上”，执行下、左、右三个方向的扩展

        }

        return null;



    }

 

（二）A*搜索算法

        A*搜索算法相对于全局择优算法改动非常小，只增加了个别函数，因此在此处省略。

（三）宽度优先算法

        宽度优先算法是一种盲目搜索算法，即，蛮力法；需要一个Open表，把起始节点放入Open表中，如果Open表为空，则无解并退出，否则，继续把第一个节点n从Open表中移除，并放入CLOSED扩展节点表中。这里要考察节点n是不是目标节点，如果是的话，就代表求出答案了，则可以退出，如果节点n往下不可以接着扩展了，那么转到第二步，继续从OPEN表中选节点，放入CLOSED表考察。如果节点n可扩展，则把所有n的子节点放入OPEN表的尾部，配置父节点指针，继续转Step2开始下一轮判断。算法流程如表 7所示。WideSearch2函数如下所示：

public int[][][] WideSearch2(long info[],int[][] num_Begin,int[][] num_Finish) {

    int[][][] result = {};

    starTime = System.nanoTime();

    Vector<Node> OPEN = new Vector<Node>();//声明不定长数组
    Vector<Node> CLOSED = new Vector<Node>();

    // 把初始节点送入OPEN表
    OPEN.add(new Node(num_Begin, 0, evaluateService.ReverseNumber(num_Begin), 0, null, 0));

    //初始节点是否是目标节点？
    if(isEqual(OPEN.get(0).num,num_Finish)){

        String s = "-----第1步-----\n";

        for (int k = 0; k < 3; ++k) {
            for (int j = 0; j < 3; ++j) {
                s += CLOSED.lastElement().num[k][j] + "  ";
                //最后一个元素的节点数据
                result[0][k][j] = CLOSED.lastElement().num[k][j];
            }
            s += "\n";
        }
        s += "-----结束-----\\n";
        info[0] = 0; // 移动步数
        info[1] = System.nanoTime() - starTime;

        return result;
    }

    while (!OPEN.isEmpty()) {

        // 计算可达性,限制搜索深度
        if (!isAvailable(OPEN.get(0).num,num_Finish) || OPEN.get(0).depth > MAX_SEARCH_DEPTH) {
            return null;
        }

        CLOSED.add(OPEN.get(0));
        OPEN.remove(0);

        int i = 0, j = 0;

        // 找到空格
        for (int k = 0; k < 9; ++k) {
            if (CLOSED.lastElement().num[k / 3][k % 3] == 0) {
                i = k / 3;
                j = k % 3;
                break;
            }
        }

        int dir = CLOSED.lastElement().direction, dep = CLOSED.lastElement().depth;
        int a[][] = new int[3][3];

        // 1 上
        if (i != 0 && dir != 2) {

            for (int m = 0; m < 3; ++m) {
                for (int n = 0; n < 3; ++n) {
                    a[m][n] = CLOSED.lastElement().num[m][n];
                }
            }

            a[i][j] = a[i - 1][j];
            a[i - 1][j] = 0;

            Node temp = new Node(a, dep + 1, evaluateService.ReverseNumber(a), 1, CLOSED.lastElement(), 0);

            // 子节点是否是目标节点？
            if (isEqual(temp.num,num_Finish)) {
                return Route2(temp, info);
            }
            OPEN.add(temp);

        }
        //参照“1 上”，执行下、左、右三个方向的扩展

 
    }

    return null;

}

【实验结果与分析】

一、执行逻辑

介绍	运行截图
初始化界面由九宫格的初始状态和目标状态、估值函数选择区、算法选择区、路径打印区、结果记录表组成。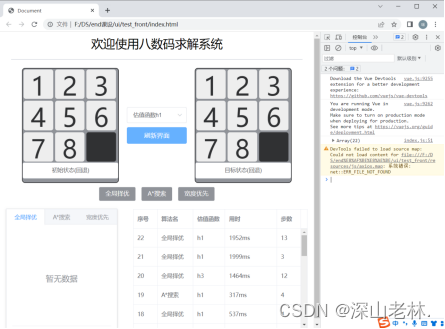
打乱九宫格后，点击“全局择先”按钮，跳出confirm框，询问是否确定进行路径查找。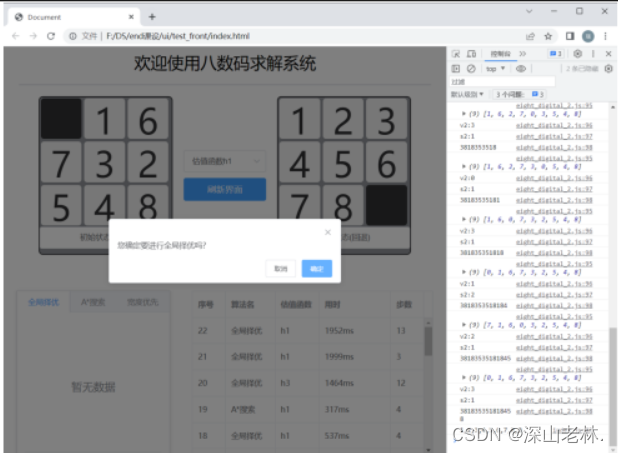
选择确定后，打印出初始状态到目标状态需要走的步数，显示在标签页内嵌的表格中。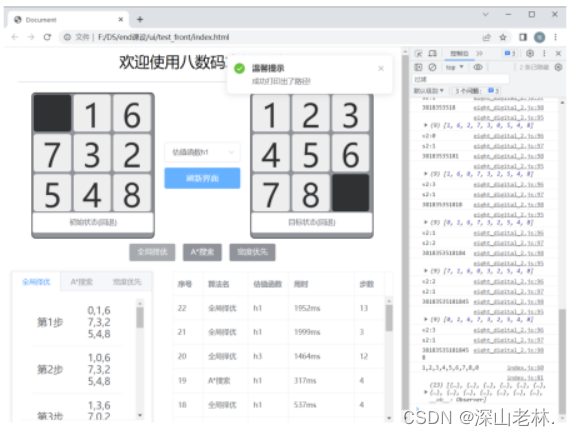
刷新界面后数据会从数据库回显到表格中，三种算法、四种估值函数均可用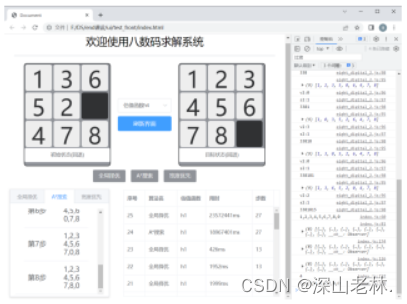

 

 

二、结果测试

信息	测试截图
--测试用例1       全局择先 h1 10步 132ms
--测试用例2         全局择先 h2 10步 166ms
--测试用例3         A*搜索 h3 10步 319ms
--测试用例4         宽度优先 10步 655ms

 

三、结果分析

从上面的对比结果来看可以得到以下的结果分析：

1. 选取不同的估值函数，有时还是会得到相同的路径结果；
2. A*搜素和全局择先的运行速度比较接近；
3. 在初始状态和目标状态相同的情况下，宽度优先的效率低于两种启发式搜索算法，即全局择先和A*算法。

 

【总结】

        现在是凌晨3点20，课设报告终于收尾了，回想这几天的课设制作，也确实是感想颇深。

    我是上周四开始写课设的，第一天，当然是储备基础知识，像典型的A*算法，还有全局择先，宽度优先这些，都认真学了一遍。当然还构思了一下课设的思路，因为不限语言，不限技术，脑子里一大堆天马行空的想实现的东西，一开始设计是想对比三种算法的优劣+用深度学习的方法训练一下它去玩这个华容道，看看到底是跑出个什么东西，或者就是想做一个联网的平台，可以让用户自行在网站pk拼图速度，或是打乱让用户还原，比较看和三种算法相比，谁的还原步数少。还想了一个点子就是用户自行上传图片––>裁剪成九宫格的样子––>玩自定义拼图，但都碍于时间有限，就没做了。

    当然，由于我目前为止主要学过的也是全栈开发，所以，在这次的课设中，最终呈现的效果，就是一个前后端交互的网页端系统了。

    周五，写课设的第二天，想着把后端架子先搭好，结果一下是pom出问题，找半天发现是maven仓库路径写错了，一下又是springboot报错，找半天，然后对着重新敲一遍就又可以运行了，气得我肝疼。好不容易加载出Spring标标了，结果又因为tomcat配的是2.9.5以上版本，配高了它有些东西不认识，又得重新写配置，总而言之就是突然发现，从头搭一个Springboot项目，对经验不丰富的人确实挺困难的呐。

     然后下午的时候，开始写逻辑，数据库如果做了实时回显的话，倒也不会显得我那张记录存储表那么没用，还是遇到了很玄学的问题，局部刷新不了+数据回显它只读第一次的，后面无法修改数据+reload整个界面又把我的路径给刷没了，所以最后这个问题就没解决了，后期有时间的话还是做成分页，elementui里倒是有个el-pagenation，今天试了绑定不了数据就没做了，下次有时间再试试。

    总之，后端遇到的困难主要是搭框架，还有就是写算法逻辑的问题，估值函数还挺好写的，三个算法对着流程图敲就完了，但一开始设计的时候，图方便，设计的字符串输出，结果就是，前端写完之后，改的我肝疼。

    分别测试了三种接口写法，一种是String直接打印结果的，非常丑，而且，不好裁。第二种是返回的三维数组，相当于是吧每种状态都存在了数组中，而每种状态本身就是个二维数组，但因为用了是数组，数组就肯定定长，定长没排满，结果就是一堆0，太心累了，找了一堆办法没裁好，最后想着，要不要就还是用Node存储Service层返回的结果，结果因为设计的问题，它递归了，嵌套了十几二十层，才能找到最里面的节点，前端拿到的json文件，一看，我是真束手无策。最后求助大佬，大佬用三维数组的那个接口，给我裁好了，但我还是追求界面美观，于是又花了一个多小时，把路径结果从直线存成了3x3的了。

    然后第三天，周六，开始写前端。前端倒是没啥难点，九宫格是改的一个4x4华容道，把人家网页扒下来，把4x4的逻辑看明白之后改成3x3的了，改这个是真挺累的，4x4的逻辑都是n%4，n÷4，那3x3就是把4改成3？no，4x4的九宫格，可移动也是4个方向，直接改的话肯定是出问题的，逻辑就是一定要能大致看得懂。我主要是卡在了回退函数那里，他那写的是n*3-v啥的，心想，3？这还不对，结果就是，这个用来记录的是移动方向和步数，3x3方格中一共有8种移动方式，所以就是0-8，并且移动两格和移动一格，对plc的修改存在一个二倍关系的，所以swith到break的排序还有要求。不过还得是我，总算还是写出来了。

    总之最后呈现的课设效果还算不错，美中不足就是，数据库到最后还是没做到实时回显，数据库在设计的时候缺乏对初始状态和终止状态的记录，and没写自定义拼图这个功能了，还有canvas实现自动还原或打乱九宫格这个功能其实也是有必要的，但也没写了。还有设计实体类的时候，忘屏蔽变量了，全public是非常不安全的做法。

   但感觉自己写的还是可以的，这应该也是我再次挑战自我，3天一个Springboot项目，离全栈工程师又近了一步。并且，通过这次的课设，也学习到了贪心、启发式搜索等算法，相信这些都会给我未来的学习带来收获。

    最后，课设做完了，感谢老师这学期的辛苦教导！