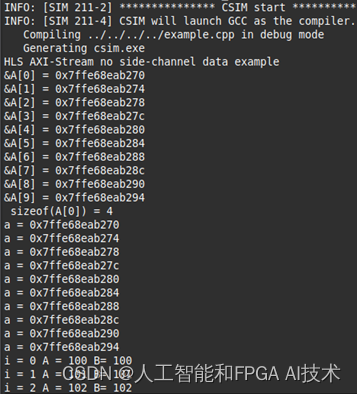
【程序员面试金典】面试题 17.21. 直方图的水量
- 题目描述
- 解题思路
题目描述
描述:给定一个直方图(也称柱状图),假设有人从上面源源不断地倒水,最后直方图能存多少水量?直方图的宽度为 1。

上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的直方图,在这种情况下,可以接 6 个单位的水(蓝色部分表示水)。 感谢 Marcos 贡献此图。
示例:
输入: [0,1,0,2,1,0,1,3,2,1,2,1]
输出: 6
解题思路
思路:最直观的想法是,当前直方图所能存储水量等于左边最大值和右边最大值之间的最小值减去当前高度,直方图的水量即所有直方图的水量之和。首先分别前向遍历、后向遍历求出当前直方图左边(包含当前)、右边(包含当前)的最大值,然后再前向遍历求出当前直方图水量即可。
int trap(vector<int>& height)
{
int n=height.size();
//特殊判断
if(n==0)
return 0;
//存储当前元素左边(包含当前)的最大值
vector<int> left(n,0);
//存储当前元素右边(包含当前)的最大值
vector<int> right(n,0);
left[0]=height[0];
right[n-1]=height[n-1];
for(int i=1;i<n;i++)
left[i]=max(left[i-1],height[i]);
for(int i=n-2;i>=0;i--)
right[i]=max(right[i+1],height[i]);
int res=0;
//所能存储水量等于左边最大值和右边最大值之间的最小值减去当前高度
for(int i=0;i<n;i++)
res+=min(left[i],right[i])-height[i];
return res;
}
总结:注意,之所以包含当前,是为了方便计算,因为有可能当前就是最高的。