【线性代数】快速复习笔记

news2025/1/12 6:58:26

线性代数快速复习

  • 行列式
    • 行列式的基础计算
      • 某行（列加上或减去另一行（列的几倍，行列式不变
      • 某行列乘k,等于k乘此行列式
      • 互换两行列，行列式变号
    • 行列式的性质
      • 1 主对角线是X，其余是其他常数a
      • 2 范德蒙德行列式
      • 3 行列式加减法
      • 4 余子式M和代数余子式A
      • 5 利用代数余子式计算行列式的值
      • 6 多个A或M相加减
      • 7 解齐次与非齐次方程组
  • 矩阵
    • 矩阵相乘
      • 基本运算
      • 单位矩阵及其他注意事项
      • 矩阵的绝对值
    • 其他
      • 转置矩阵
      • 证明矩阵可逆
      • 求逆矩阵
      • 利用逆矩阵进行矩阵乘法运算
      • 伴随矩阵
      • 矩阵的秩
  • 向量组与线性空间
    • 线性表示（矩阵和增广矩阵秩相等）
    • 向量组线性相关（组成的矩阵秩小于向量个数）
    • 求向量在某基底坐标
    • 求极大无关组
  • 解方程组
    • 判断解的情况
    • 解方程组
      • 特解、通解、基础解系
      • 已知多个非齐次特解求齐次通解
      • 线性无关的解个数
  • 方阵对角化及应用
    • 规范正交化
    • 求特征值
    • 特征向量
    • 与对角阵相似
  • 二次型
    • 系数矩阵
    • 化为标准型（用特征值求）
    • 化为规范形
    • 配方法化为标准型
    • 正定矩阵

行列式

行列式的基础计算

某行（列加上或减去另一行（列的几倍，行列式不变

在这里插入图片描述

某行列乘k,等于k乘此行列式

在这里插入图片描述

互换两行列，行列式变号

在这里插入图片描述

在这里插入图片描述

计算的书写步骤和规范
在这里插入图片描述

行列式的性质

1 主对角线是X，其余是其他常数a

在这里插入图片描述

2 范德蒙德行列式

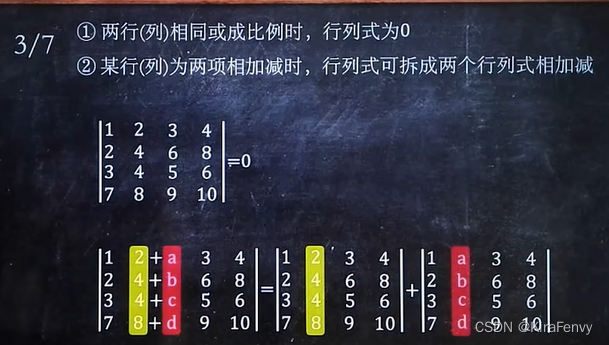
在这里插入图片描述

3 行列式加减法

在这里插入图片描述
例题：
在这里插入图片描述

4 余子式M和代数余子式A

在这里插入图片描述

5 利用代数余子式计算行列式的值

在这里插入图片描述

6 多个A或M相加减

在这里插入图片描述
在这里插入图片描述

7 解齐次与非齐次方程组

齐次方程组没有常数项，而非齐次有
在这里插入图片描述

在这里插入图片描述

矩阵

矩阵相乘

基本运算

前行乘后列，以前面的行数和后面的列数确定结果行列数，而前面的列数和后面的行数需要相等才能相乘
在这里插入图片描述

单位矩阵及其他注意事项

注意矩阵乘法满足分配律但不满足交换律

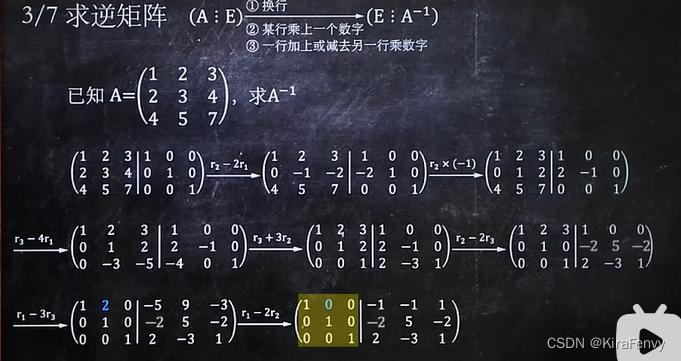
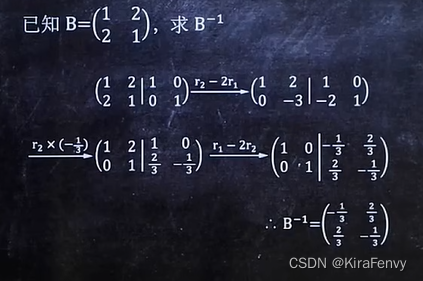
在这里插入图片描述

在这里插入图片描述

矩阵的绝对值

在这里插入图片描述

其他

转置矩阵

在这里插入图片描述

证明矩阵可逆

在这里插入图片描述
在这里插入图片描述

求逆矩阵

在这里插入图片描述
在这里插入图片描述

利用逆矩阵进行矩阵乘法运算

在这里插入图片描述

伴随矩阵

在这里插入图片描述

矩阵的秩

在这里插入图片描述

其实只要0的数量递增就行，不用最后一行一定全是0，此时R(A)=3
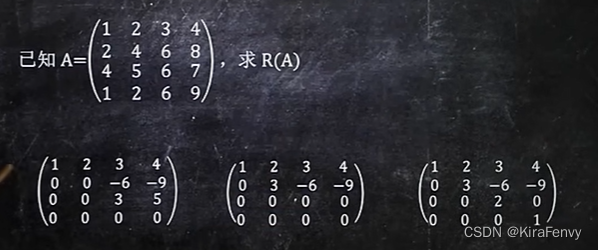
在这里插入图片描述
在这里插入图片描述

向量组与线性空间

线性表示（矩阵和增广矩阵秩相等）

在这里插入图片描述

向量组线性相关（组成的矩阵秩小于向量个数）

在这里插入图片描述

求向量在某基底坐标

在这里插入图片描述

求极大无关组

在这里插入图片描述

解方程组

判断解的情况

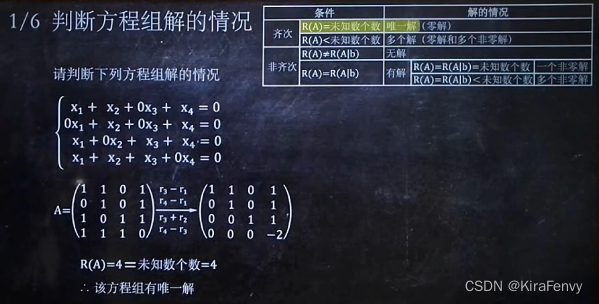
在这里插入图片描述

齐次示例：

在这里插入图片描述
非齐次示例
在这里插入图片描述

解方程组

例1：
在这里插入图片描述
例2：
在这里插入图片描述
如果是齐次：
在这里插入图片描述

特解、通解、基础解系

特解
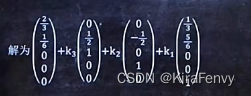
在这里插入图片描述

通解
在这里插入图片描述

基础解系
在这里插入图片描述

已知多个非齐次特解求齐次通解

在这里插入图片描述

下面的X1和X2不成比例，所以线性无关

线性无关的解个数

在这里插入图片描述

方阵对角化及应用

规范正交化

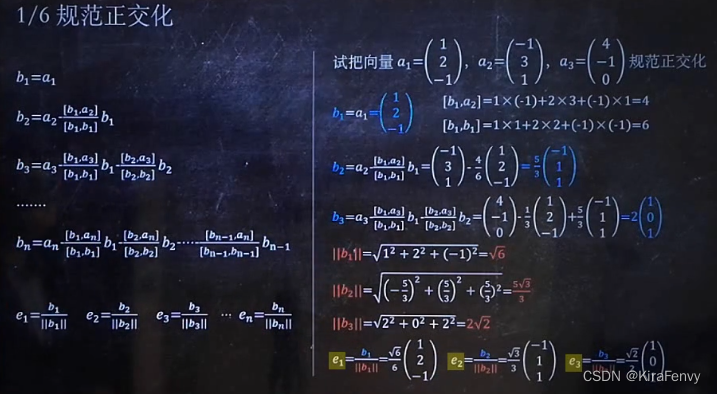
在这里插入图片描述

求特征值

在这里插入图片描述

特征向量

在这里插入图片描述

与对角阵相似

在这里插入图片描述

在这里插入图片描述
在这里插入图片描述

二次型

系数矩阵

在这里插入图片描述

化为标准型（用特征值求）

在这里插入图片描述

化为规范形

在这里插入图片描述

配方法化为标准型

在这里插入图片描述

正定矩阵

在这里插入图片描述
在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/703946.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Linux中安装配置启动Redis

Linux中安装配置启动Redis

Linux中安装配置启动Redis 一、下载redis 使用命令下载： wget https://download.redis.io/releases/redis-6.0.10.tar.gzls du sh redis-6.0.10.tar.gz解压 [rootnode02 ~]# tar xzf redis-6.0.10.tar.gz [rootnode02 ~]# cd redis-6.0.10 [rootnode02 redis-6.…
阅读更多...
低代码：改变未来的智慧力量！打造智能产业新纪元！

低代码：改变未来的智慧力量！打造智能产业新纪元！

前言 在数智时代的浪潮中，智慧产业成为推动经济发展的重要引擎。随着科技的不断进步，传统工厂也在加速转型为智能工厂，实现产业体系的智能化建设已经成为当今企业追求的目标。 概念 产业体系智能化是指借助信息技术手段，对传统产业…
阅读更多...
redis高可用（二）

redis高可用（二）

redis高可用（二） 一、主从复制 1.概念 主从复制，是指将一台Redis服务器的数据，复制到其他的Redis服务器。前者称为主节点(Master)，后者称为从节点(Slave)；数据的复制是单向的，只能由主节点到…
阅读更多...
Dlib —— 对图片进行人脸检测并绘出特征（附C++源码）

Dlib —— 对图片进行人脸检测并绘出特征（附C++源码）

效果 注意&#xff1a;Dlib检测人脸在Release版耗时与CPU有关,本人I7 10代约100ms左右。建议人脸检测可以考虑使用Yolov5进行&#xff0c;之后将检测到的人脸输入给Dlib做特征或其他。 代码 #include <iostream>#include <dlib/image_processing/frontal_face_detecto…
阅读更多...
【胖虎的逆向之路】——GOT/PLT Hook详解针对自定义so库的Hook实操

【胖虎的逆向之路】——GOT/PLT Hook详解针对自定义so库的Hook实操

文章目录 [TOC](文章目录) 前言一、ELF 是什么&#xff1f;1、ELF 的概念2、ELF 的组成2.1、 两种视图是什么呢&#xff1f;2.2、 ELF文件头又是什么西西&#xff1f;2.2、 ELF中节头表是什么南南呢&#xff1f;2.2、 ELF中程序头表是什么北北呢&#xff1f; 二、动态库装载、动…
阅读更多...
uni-app 微信小程序发布时，主包超过2M限制

uni-app 微信小程序发布时，主包超过2M限制

小程序发布时&#xff0c;提示超过2M&#xff0c;无法通过&#xff0c;此时可以尝试以下几种方法&#xff1a; 1、对图片做压缩 图片尽量放在服务器端&#xff0c;使用的时候&#xff0c;通过URL路径获取&#xff0c;若不得已放在本地时&#xff0c;可以对图片进行压缩&#…
阅读更多...
基于springboot+Redis的前后端分离项目之分布式锁-redission（五）-【黑马点评】

基于springboot+Redis的前后端分离项目之分布式锁-redission（五）-【黑马点评】

&#x1f381;&#x1f381;资源文件分享 链接&#xff1a;https://pan.baidu.com/s/1189u6u4icQYHg_9_7ovWmA?pwdeh11 提取码&#xff1a;eh11 分布式锁-redission 分布式锁-redission1 分布式锁-redission功能介绍2 分布式锁-Redission快速入门3 分布式锁-redission可重入锁…
阅读更多...
NoSQL之Redis优化（一）

NoSQL之Redis优化（一）

Redis的高可用 一、Redis 持久化RDB 持久化AOF 持久化RDB和AOF的优缺点 二、Redis 性能管理内存碎片如何产生的&#xff1f;解决碎片率大的问题&#xff1a;内存使用率内回收key 在web服务器中&#xff0c;高可用是指服务器可以正常访问的时间&#xff0c;衡量的标准是在多长时…
阅读更多...
【Java可执行命令】（四）反编译工具javap：深入解析应用程序反编译工具javap ~

【Java可执行命令】（四）反编译工具javap：深入解析应用程序反编译工具javap ~

Java可执行命令详解之javap 1️⃣ 概念2️⃣ 优势和缺点3️⃣ 使用3.1 语法格式3.1.1 可选参数&#xff1a;-l3.1.2 可选参数&#xff1a;-c3.1.3 可选参数&#xff1a;-s3.1.4 可选参数&#xff1a;-verbose3.1.5 可选参数&#xff1a;-version 4️⃣ 应用场景5️⃣ 注意事项&…
阅读更多...
6.21、设计模式 单例设计模式

6.21、设计模式 单例设计模式

1 设计模式&#xff08;Design pattern&#xff09; 代表了最佳的实践&#xff0c;通常被有经验的面向对象的软件开发人员所采用。设计模式是软件开发人员在软件开发过程中面临的一般问题的解决方案。这些解决方案是众多软件开发人员经过相当长的一段时间的试验和错误总结出来…
阅读更多...
好用又智能笔记类工具有哪些？

好用又智能笔记类工具有哪些？

在工作和生活中&#xff0c;我们经常面临大量信息和任务需要记录和整理。好用又智能的笔记类工具成为了办公人士提高工作效率和组织信息的必备利器。 敬业签笔记工具支持分类记录笔记&#xff0c;可以根据不同的主题或项目进行整理。无论是工作笔记、学习笔记还是个人生活记录…
阅读更多...
OpenFeign——请求其他服务时传递token信息

OpenFeign——请求其他服务时传递token信息

文章目录 前言准备流程初测定义nacos-product子服务定义服务的消费方 cloudalibaba-openfeign-server初步测试结论 设置cloudalibaba-openfeign-server中的feign总结 前言 在实际开发过程中&#xff0c;服务与服务之间都会有比较频繁的通信操作。其次不同用户所需要查询的数据…
阅读更多...
【正点原子STM32连载】 第四十七章 SRAM实验 摘自【正点原子】STM32F103 战舰开发指南V1.2

【正点原子STM32连载】 第四十七章 SRAM实验 摘自【正点原子】STM32F103 战舰开发指南V1.2

1&#xff09;实验平台&#xff1a;正点原子stm32f103战舰开发板V4 2&#xff09;平台购买地址&#xff1a;https://detail.tmall.com/item.htm?id609294757420 3&#xff09;全套实验源码手册视频下载地址&#xff1a; http://www.openedv.com/thread-340252-1-1.html# 第四…
阅读更多...
使用inno打包程序流程

使用inno打包程序流程

1:配置iss文件 ​​​​​​​ 2编译 3.生成安装包文件安装
阅读更多...
浅谈建筑项目中的智能照明系统的设计与研究

浅谈建筑项目中的智能照明系统的设计与研究

【摘要】&#xff1a;建筑智能照明工程中智能照明控制系统发展迅速&#xff0c;具有舒适性和节能性两方面优势。智能照明控制系统已经处于模块化高速发展阶段&#xff0c;如今更好的控制方案成为制约系统发展的瓶颈。文章在研究了国内外智能照明系统的基础上&#xff0c;从照明…
阅读更多...
【CSS】nth:children以及浏览器内核webkit使用（滚动条样式修改）

【CSS】nth:children以及浏览器内核webkit使用（滚动条样式修改）

&#x1f609;博主&#xff1a;初映CY的前说(前端领域) ,&#x1f4d2;本文核心&#xff1a;nth:children以及浏览器中的webkit使用 前言&#xff1a;在页面的编写中使用了多个标签通常有需求去处理下特殊的样式&#xff0c;我们常见做法是给我们的标签加上一个类或者通过标签选…
阅读更多...
【微服务】什么是微服务？-- 全面了解微服务架构

【微服务】什么是微服务？-- 全面了解微服务架构

What is Microservices — Edureka 您有没有想过&#xff0c;什么是微服务以及扩展行业如何与它们集成&#xff0c;同时构建应用程序以满足客户的期望&#xff1f; 要了解什么是微服务&#xff0c;您必须了解如何将单体应用程序分解为独立打包和部署的小型微型应用程序。本文将…
阅读更多...
力扣 -- 91.解码方法

力扣 -- 91.解码方法

题目链接&#xff1a;91. 解码方法 - 力扣&#xff08;LeetCode&#xff09; 以下是用动态规划的思想解决这道题目&#xff0c;如果对动态规划五部曲的含义还不是很清楚的老铁可以看看本专栏的第一题动规(10条消息) 力扣 -- 746. 使用最小花费爬楼梯_KOBE 0824 BRYANT的博客-…
阅读更多...
软件测试编写文档模板【附文档模板】

软件测试编写文档模板【附文档模板】

一、测试岗位必备的文档 在一个常规的软件测试流程中&#xff0c;会涉及到测试计划、测试方案、测试用例、测试报告的编写&#xff0c;这些文档也是软件测试岗位必须掌握的文档类型。 1、测试计划 测试计划是组织管理层面的文件&#xff0c;从组织管理的角度对一次测试活动进…
阅读更多...
华为OD机试真题 Python实现【最小的调整次数】【2023Q1 100分】

华为OD机试真题 Python实现【最小的调整次数】【2023Q1 100分】

目录 一、题目描述二、输入描述三、输出描述四、补充说明五、解题思路六、Python算法源码七、效果展示1、输入2、输出3、说明 一、题目描述 有一个特异性的双端队列&#xff0c;该队列可以从头部或尾部添加数据&#xff0c;但是只能从头部移出数据。 小A依次执行2n个指令往队…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023