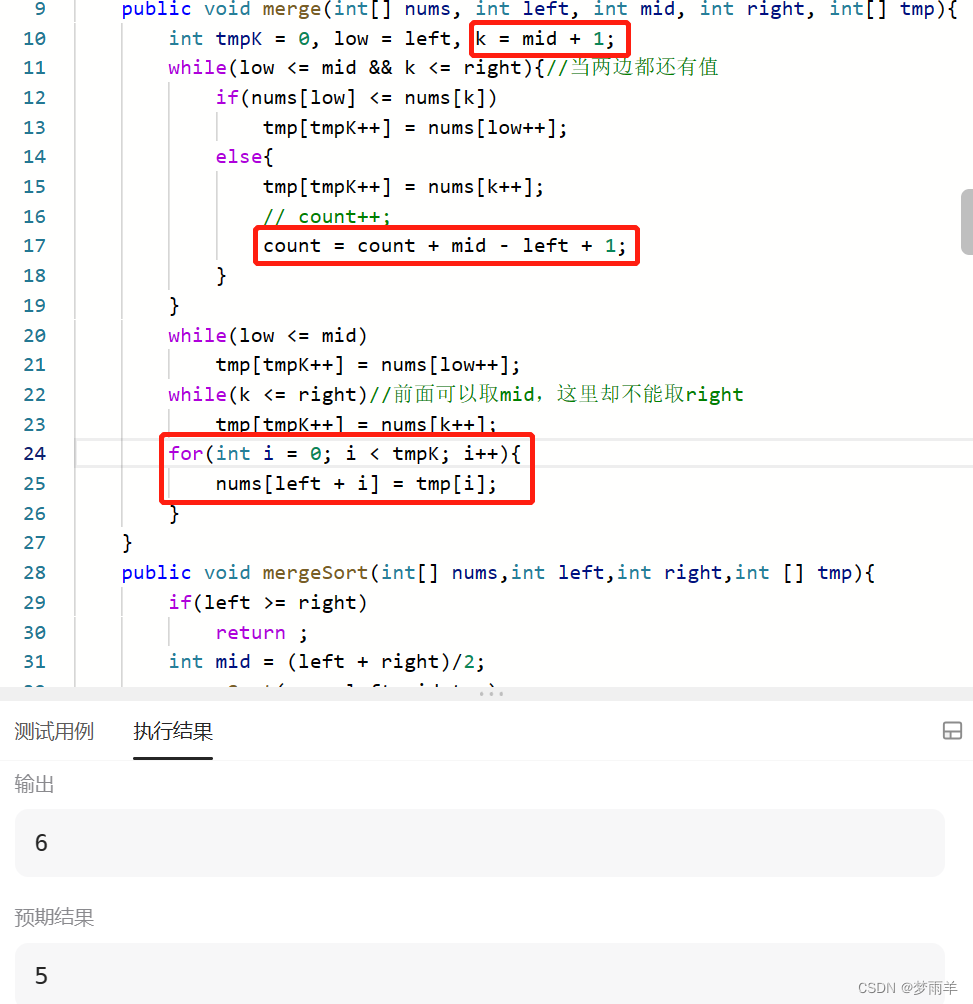
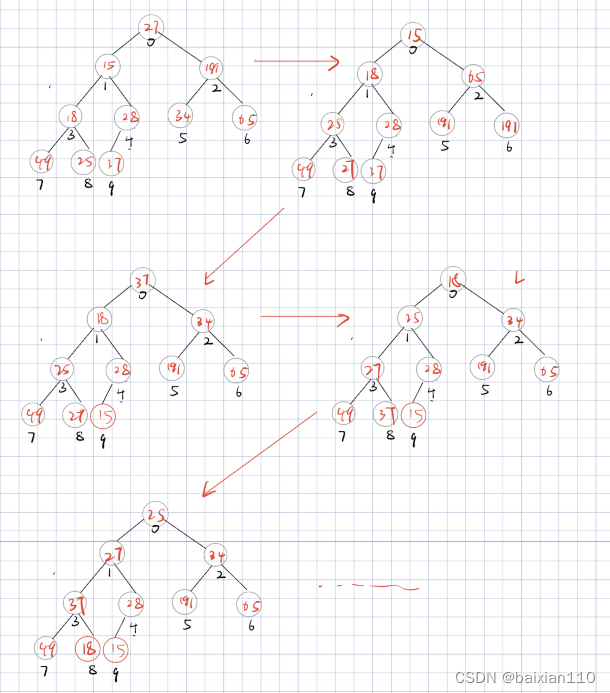
这道题归根结底就是一个归并问题，逆序对本质上就是比较大小，如果两边作为一个整体比较过那么就可以排序合并（因为这个过程每一步都计算了count的值，所以合并起来是可以的）。

下面的k应该是mid+1（从中间的右边一位开始取，不能等于）。

临时的数组十分重要，它的范围在每个循环的left到数组结尾的tmpK

 

class Solution {
    int count;
    public int reversePairs(int[] nums) {
        this.count = 0;
        int[] tmp = new int[nums.length];
        mergeSort(nums,0,nums.length-1,tmp);
        return count;
    }
    public void merge(int[] nums, int left, int mid, int right, int[] tmp){
        int tmpK = 0, low = left, k = mid + 1;
        while(low <= mid && k <= right){//当两边都还有值
            if(nums[low] <= nums[k])
                tmp[tmpK++] = nums[low++];
            else{
                tmp[tmpK++] = nums[k++];
                // count++;一个数大于其说明后面的都大于
                //只考虑从左往右的，大于直接左边右移，不用一个个加
                count = count + mid - low + 1;
            }
        }
        while(low <= mid)
            tmp[tmpK++] = nums[low++];
        while(k <= right)//前面可以取mid，这里却不能取right
            tmp[tmpK++] = nums[k++];
        for(int i = 0; i < tmpK; i++){//起始位置right到tmpK
            nums[left + i] = tmp[i];
        }
    }
    public void mergeSort(int[] nums,int left,int right,int [] tmp){
        if(left >= right)
            return ;
        int mid = (left + right)/2;
        mergeSort(nums,left,mid,tmp);
        mergeSort(nums,mid+1,right,tmp);
        merge(nums,left,mid,right,tmp);
    }
}