【LeetCode热题100】打卡第28天：不同的二叉搜索树&验证二叉搜索树&对称二叉树

⛅前言

大家好，我是知识汲取者，欢迎来到我的LeetCode热题100刷题专栏！

精选 100 道力扣（LeetCode）上最热门的题目，适合初识算法与数据结构的新手和想要在短时间内高效提升的人，熟练掌握这 100 道题，你就已经具备了在代码世界通行的基本能力。在此专栏中，我们将会涵盖各种类型的算法题目，包括但不限于数组、链表、树、字典树、图、排序、搜索、动态规划等等，并会提供详细的解题思路以及Java代码实现。如果你也想刷题，不断提升自己，就请加入我们吧！QQ群号：827302436。我们共同监督打卡，一起学习，一起进步。

LeetCode热题100专栏🚀：LeetCode热题100

Gitee地址📁：知识汲取者 (aghp) - Gitee.com

题目来源📢：LeetCode 热题 100 - 学习计划 - 力扣（LeetCode）全球极客挚爱的技术成长平台

PS：作者水平有限，如有错误或描述不当的地方，恳请及时告诉作者，作者将不胜感激

不同的二叉搜索树

🔒题目

原题链接：96.不同的二叉搜索树

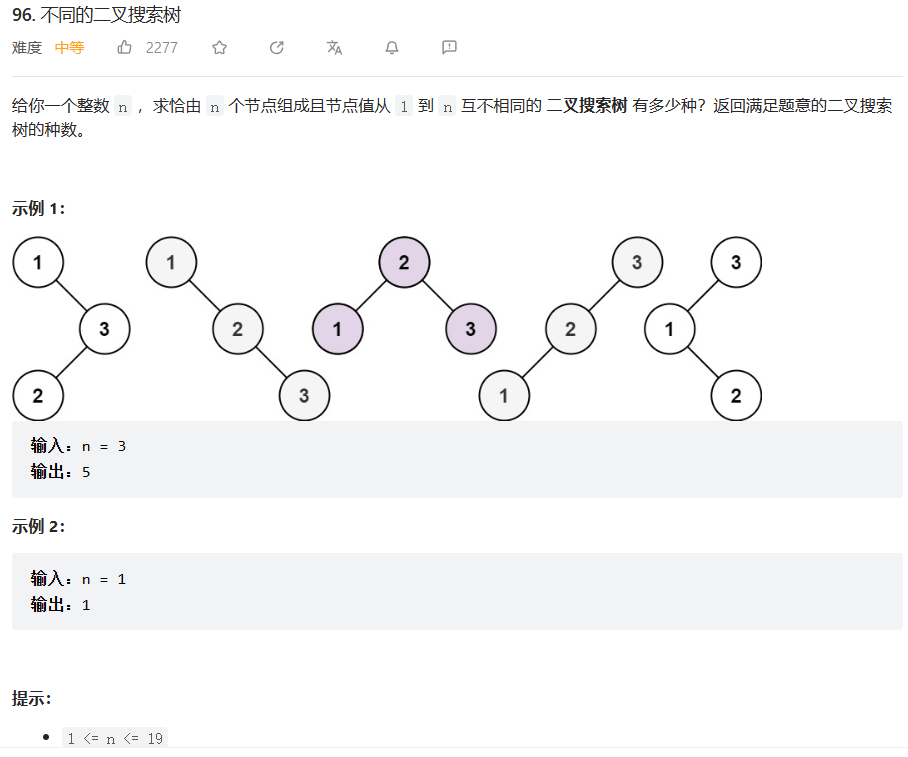
🔑题解

• 解法一：递归求解

  这题如果直接根据二叉搜索树的特性去暴力枚举，是十分复杂的，并且耗时也十分高，所以这里我们需要明确二叉搜索树的一个特点，也就是：$G(n)={\sum }_{i=1}^{n}G(i-1)\ast G(n-i)$

  PS：关于这个公式的推导可以参考LeetCode官方题解，或者自行百度，这里不做过多介绍

  通过这个公式我们可以明确，n个节点能够组成多少种二叉搜索树，现在我们只需要使用代码实现上述的公式即可

  /**
   * @author ghp
   * @title
   */
  class Solution {
      public int numTrees(int n) {
          // 递归终止条件（子树只有一个节点或者没有子树，直接返回1）
          if (n == 0 || n == 1) {
              return 1;
          }
          int count = 0;
          // 枚举以节点i为根节点时可以组成二叉树搜索树
          for (int i = 1; i <= n; i++) {
              // 计算左子树有多少种组合
              int l = numTrees(i - 1);
              // 计算右子树有多少种组合
              int r = numTrees(n - i);
              // 更新i个节点时二叉搜索树的组合总数
              count += l * r;
          }
          return count;
      }
  }
  

  复杂度分析：

  • 时间复杂度：$O(2^n)$，遍历n个节点，并且每个节点都需要递归调用两次
  • 空间复杂度：$O(n)$，需要递归调用两次，每次递归调用的层数是n，所以递归所需额外开销的空间约为2n

  这里可能你会好奇为什么当前第 i 个节点的二叉搜索树的组合总数 l*r (●’◡’●)，因为，左边每一种组合都可以对应右边r种组合，所以这里第 使用节点为 i 为根节点时，总的组合数为 l*r，然后还需要加上前面 计算出来的总和，所以当前 i 个节点，能够组成二叉搜索数的组合数计算公式是 count += l*r

  代码优化：空间换时间

  上面代码存在大量重复计算，左右子树可能节点数量相同，左右子树节点相同时，计算是相同的，所以我们可以使用一个Map集合存储当前节点数量的组合，这样当我们遇到相同节点时，就可以直接使用之前计算的，从而避免了重复计算（这个过程类似于记忆化搜索），同时也能避免很多重复性的递归

  import java.util.HashMap;
  import java.util.Map;
  
  /**
   * @author ghp
   * @title
   */
  class Solution {
      Map<Integer, Integer> map = new HashMap<>();
  
      public int numTrees(int n) {
          // 递归终止条件（子树只有一个节点或者没有节点，直接返回1）
          if (n == 0 || n == 1) {
              return 1;
          }
          if (map.containsKey(n)) {
              // 当前节点节点，已被计算过了，直接返回之前计算的计算结果
              return map.get(n);
          }
          int count = 0;
          // 枚举以节点i为根节点时可以组成二叉树搜索树
          for (int i = 1; i <= n; i++) {
              // 计算左子树有多少种组合
              int l = numTrees(i - 1);
              // 计算右子树有多少种组合
              int r = numTrees(n - i);
              // 更新二叉搜索树的组合总数
              count += l * r;
          }
          // 将当前节点的计算记过存储到map集合种
          map.put(n, count);
          return count;
      }
  }
  

  优化前：

  

  优化后：

  

• 解法二：动态规划

  从前面我们给出的那个公式，我们也可以很明显的发现，这就是一个典型的动态转移方程，所以肯定是可以使用动态规划来实现的

  /**
   * @author ghp
   * @title
   */
  class Solution {
      public int numTrees(int n) {
          int[] g = new int[n + 1];
          g[0] = 1;
          g[1] = 1;
          for (int i = 2; i < g.length; i++) {
               for (int j = 1; j <= i; j++) {
                  g[i] += g[j - 1] * g[i - j];
              }
          }
          return g[n];
      }
  }
  

  复杂度分析：

  • 时间复杂度：$O(n^2)$
  • 空间复杂度：$O(n)$

  其中 $n$ 为数组中元素的个数

• 解法三：公式法

  可以直接使用$C_n=\frac{2(2n+1)}{n+2}{C}_{n-1}$进行计算，满足这个递推式的数称之为卡特兰数

  class Solution {
      public int numTrees(int n) {
          // 提示：我们在这里需要用 long 类型防止计算过程中的溢出
          long count = 1;
          for (int i = 0; i < n; ++i) {
              count = count * 2 * (2 * i + 1) / (i + 2);
          }
          return (int) count;
      }
  }
  

  题解来源：不同的二叉搜索树 - 不同的二叉搜索树 - 力扣（LeetCode）

验证二叉搜索树

🔒题目

原题链接：98.验证二叉搜索树

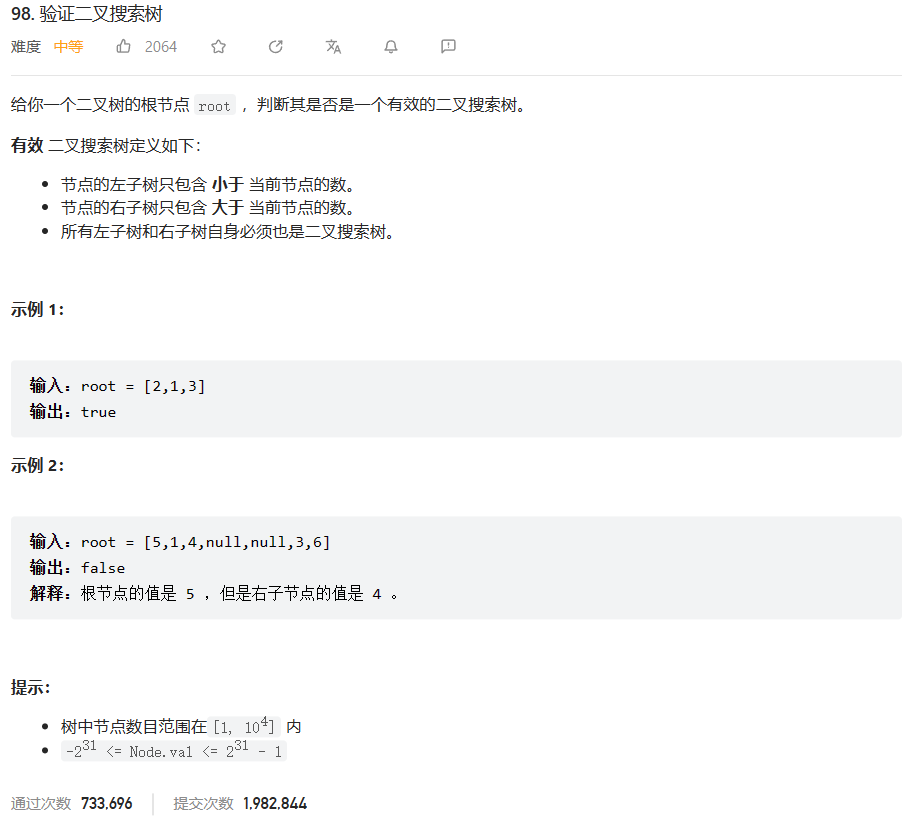
🔑题解

• 解法一：递归

  递归的思路比较简单，需要满足左子树是严格递减的，右子树是严格递增的，这里需要使用两个变量来记录当前的较小值，也就是说对于左子树要求当前的值比当前最小值还要小，对于右子树要求当前的值比当前最大的值还要大

  注意：这里有一个特别坑的地方，提示中有 $-2^{31}<=Node.val<=2^{31}-1$，节点的值是可以取到 int 的最大值和最小值，所以这里初始化最大值和最小值，一定不能使用 Integer.MIN_VALUE和Integer.MAX_VALUE，这样会导致在进行 if 判断时，可以取等，从而导致 false ，为了避免边界值的情况，我们需要使用 Long.MIN_VALUE 和 Long.MAX_VALUE进行初始化

  /**
   * @author ghp
   * @title
   */
  public class Solution {
  
      public boolean isValidBST(TreeNode root) {
          return isBinarySearchTree(root, Long.MIN_VALUE, Long.MAX_VALUE);
      }
  
      private boolean isBinarySearchTree(TreeNode root, long smaller, long bigger) {
          if (root == null) {
              // 到底了，直接返回true
              return true;
          }
          if (root.val <= smaller || root.val >= bigger){
              // 左子树或右子树不符合要求
              return false;
          }
          // 遍历左子树，判断左子树是否严格递减
          boolean f1 = isBinarySearchTree(root.left, smaller, root.val);
          // 遍历右子树，判断右子树是否严格递增
          boolean f2 = isBinarySearchTree(root.right, root.val, bigger);
          // 左子树和右子树都需要满足才是一颗二叉搜索树
          return f1 && f2;
      }
  }
  

  复杂度分析：

  • 时间复杂度：$O(n)$
  • 空间复杂度：$O(n)$

  其中 $n$ 为数组中元素的个数

• 解法二：中序遍历

  这个解法是从二叉搜索树中序遍历的特点出发的，二叉搜索树中序遍历得到的是一个严格递增的数列，我们只需要对二叉树进行中序遍历，并判断中序遍历得到的数列是否是按照严格递增的，即可判断当前这颗二叉树是否是二叉搜索树

  • 递归写法：

    public class Solution {
    
        private long pre = Long.MIN_VALUE;
        
        public boolean isValidBST(TreeNode root) {
            return traversal(root);
        }
    
        private boolean traversal(TreeNode root) {
            if (root == null) {
                return true;
            }
            // 遍历左节点
            boolean f1 = traversal(root.left);
            if (root.val <= pre){
                // 当前节点的值不符合严格递增
                return false;
            }
            // 记录上一个节点
            pre = root.val;
            // 遍历右节点
            boolean f2 = traversal(root.right);
            return f1 && f2;
        }
    }
    

    复杂度分析：

    • 时间复杂度：$O(n)$
    • 空间复杂度：$O(n)$

    其中 $n$ 为数组中元素的个数

  • 迭代写法：

    public class Solution {
        public boolean isValidBST(TreeNode root) {
            Deque<TreeNode> stack = new ArrayDeque<>();
            TreeNode cur = root;
            long pre = Long.MIN_VALUE;
            boolean f = true;
            while (!stack.isEmpty() || cur != null) {
                while (cur != null) {
                    stack.push(cur);
                    cur = cur.left;
                }
                TreeNode node = stack.pop();
                if (node.val <= pre) {
                    return false;
                }
                pre = node.val;
                cur = node.right;
            }
            return f;
        }
    }
    

    PS：如果对上面这个迭代写法不是很懂的话，可以参考博主的这篇文章：【LeetCode热题100】打卡第27天：二叉树的遍历

对称二叉树

🔒题目

原题链接：101.对称二叉树

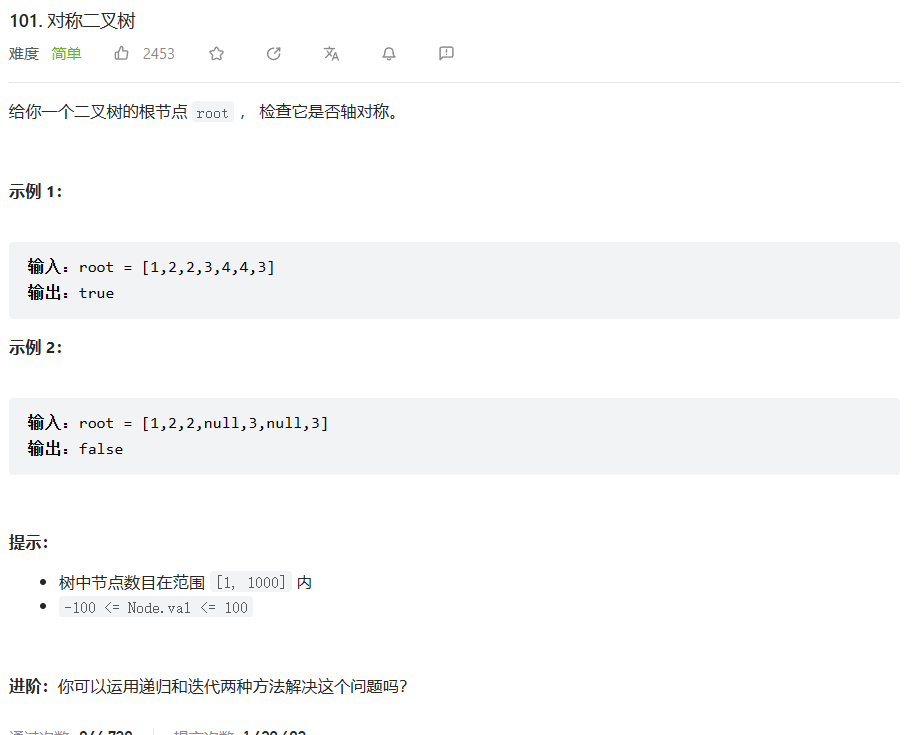
🔑题解

最开始想使用中序遍历来解决，但是失败了，对于[5,4,1,null,1,null,4,2,null,2,null]无法通过！

class Solution {
    public boolean isSymmetric(TreeNode root) {
        Deque<TreeNode> stack = new ArrayDeque<>();
        TreeNode cur = root;
        StringBuilder sb = new StringBuilder();
        while (!stack.isEmpty() || cur != null) {
            while (cur != null) {
                stack.push(cur);
                cur = cur.left;
            }
            TreeNode node = stack.pop();
            if (node.right != null && node.left == null) {
                sb.append(0);
            }
            sb.append(node.val);
            cur = node.right;
            if (node.left != null && node.right == null) {
                sb.append(0);
            }
        }
        String str1 = new String(sb);
        System.out.println(str1);
        String str2 = new String(new StringBuilder(sb).reverse());
        return str1.equals(str2);
    }
}

• 解法一：递归

  也就是左右同时遍历，这里需要使用两个类似于指针的引用，left和right，left遍历根节点的左子树，right遍历根节点的右子树。最后通过层层的判断，我们可以判断整个二叉树是否对称

  PS：可能是题目写的有点少，一开始我还想到，但是一看题解就恍然大悟w(ﾟДﾟ)w

  

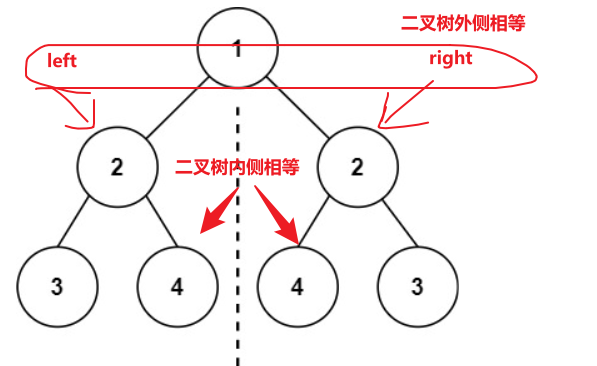
  class Solution {
      public boolean isSymmetric(TreeNode root) {
          return check(root, root);
      }
  
      /**
       * 判断二叉树是否对称
       *
       * @param left  左子树
       * @param right 右子树
       * @return
       */
      private boolean check(TreeNode left, TreeNode right) {
          if (left == null && right == null) {
              // 两者都为空，说明对称
              return true;
          }
          if (left == null || right == null) {
              // 一方为空，说明不对成
              return false;
          }
          // 单独判断根节点左右是否对称（除了第一遍，后面和f1是等价的）
          if (left.val != right.val) {
              return false;
          }
          // 判断外侧节点的值是否相同
          boolean f1 = check(left.left, right.right);
          // 判断右侧节点的值是否相同
          boolean f2 = check(left.right, right.left);
          return f1 && f2;
      }
  }
  

  复杂度分析：

  • 时间复杂度：$O(n)$
  • 空间复杂度：$O(n)$

  其中 $n$ 为数组中元素的个数