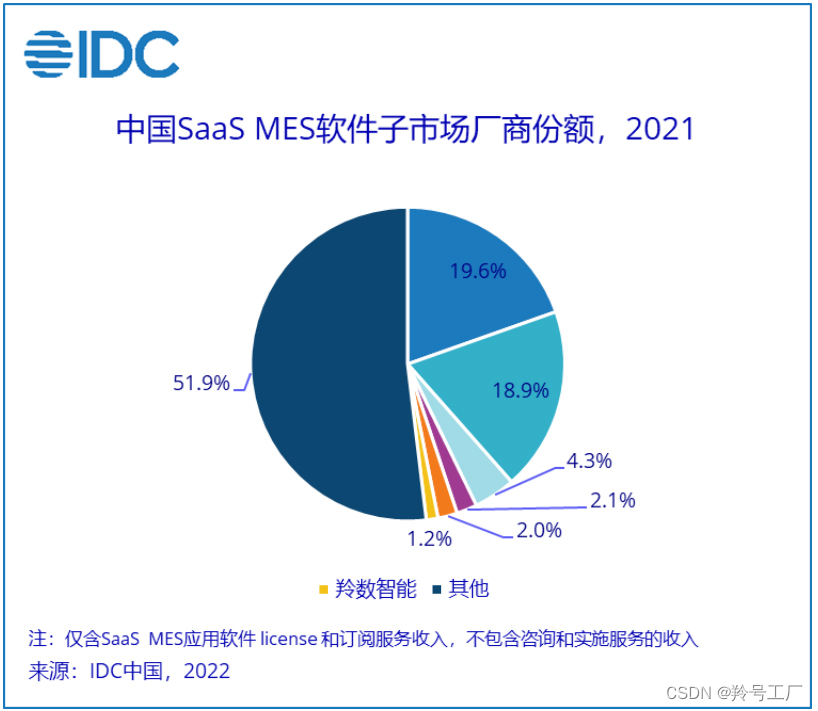
In mathematics, a partition of an interval [a, b] on the real line is a finite sequence x0, x1, x2, …, xn of real numbers such that
a = x0 < x1 < x2 < … < xn = b.
In other terms, a partition of a compact interval I is a strictly increasing sequence of numbers (belonging to the interval I itself) starting from the initial point of I and arriving at the final point of I.
Every interval of the form [xi, xi + 1] is referred to as a subinterval of the partition x.

A partition of an interval being used in a Riemann sum. The partition itself is shown in grey at the bottom, with one subinterval indicated in red.
Contents
- 1 Refinement of a partition
- 2 Norm of a partition
- 3 Applications
- 4 Tagged partitions
- 5 See also