基于Diffusion model的图像生成和重建

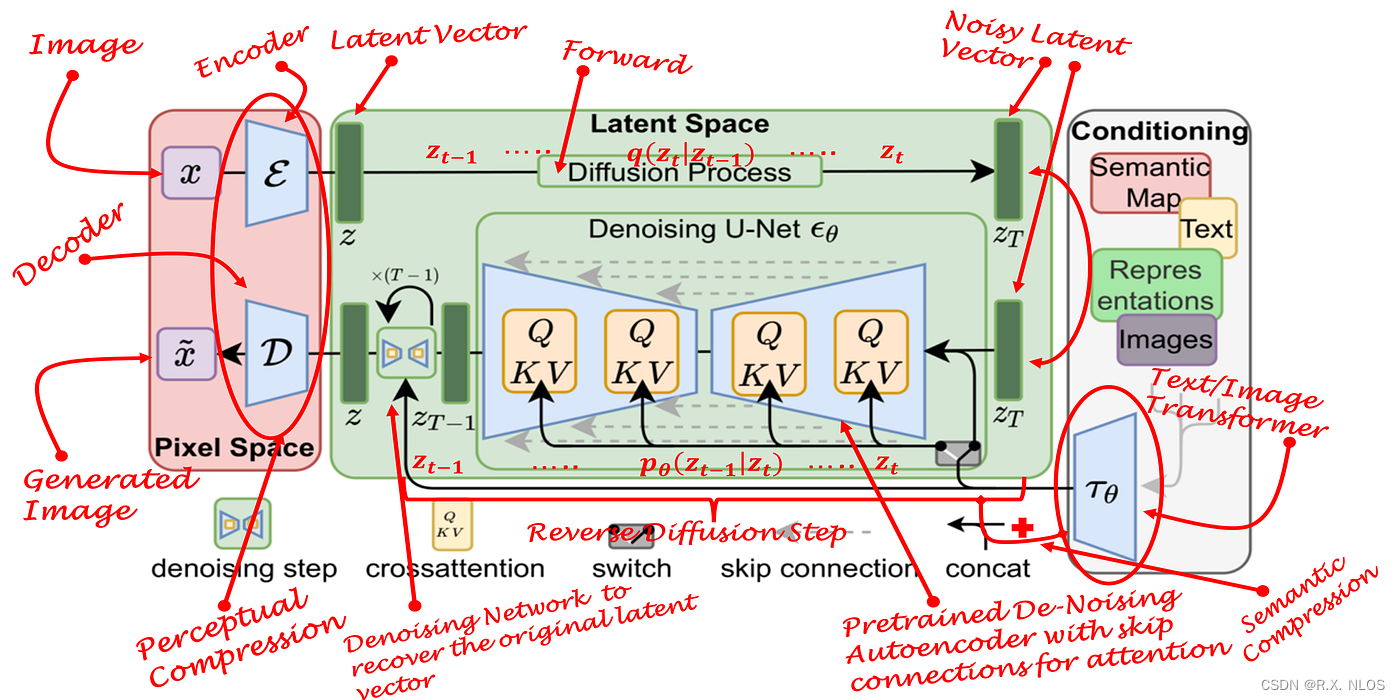
在这里插入图片描述

What are Stable Diffusion Models and Why are they a Step Forward for Image Generation? | by J. Rafid Siddiqui, PhD | Towards Data Science

本文将从概念、原理推导、研究现状、挑战和未来展望等方面，对基于Diffusion model的图像生成和重建进行详细介绍。

背景介绍

生成对抗网络（GANs）和变分自编码器（VAEs）等深度生成模型在过去几年取得了显著的成功。然而，近年来，一种名为 扩散概率模型（Diffusion Probabilistic Models，简称DPMs） 的新型生成模型因其强大的表现力和稳定的训练过程而备受关注。

在这里插入图片描述

From data to noise to data for mixing physics across temperatures with generative artificial intelligence | PNAS

DPMs的核心思想是通过将图像逐渐退化为噪声的过程（正向过程），然后再通过生成模型逐步恢复原始图像（逆向过程）来进行图像生成和重建。这种方法在图像生成和重建任务中取得了令人瞩目的性能，特别是在高分辨率图像生成和图像去噪方面。

原理介绍和推导

正向过程

扩散概率模型的核心是一个 连续时间扩散过程 。给定一个初始图像 $x_0$ ，我们将其退化为噪声图像 $x_T$ ，其中 $T$ 是扩散过程的时间长度。在每个时间步 $t$ ，我们引入一个噪声变量 $\epsilon_t$ ，对图像进行扰动：

$x_{t+1} = x_t + \sqrt{\Delta t} \cdot \epsilon_t$

其中 $\Delta t$ 是时间步长， $\epsilon_t \sim \mathcal{N}(0, I)$ 是一个独立的高斯噪声。在连续时间极限下，我们可以将整个过程表示为随机微分方程：

$dx_t = \sqrt{dt} \cdot dW_t$

其中 $W_t$ 是布朗运动。我们可以从这个过程中采样一系列中间状态 ${x_t\}_{t=0}^T$ ，然后使用条件概率密度 $p(x_{t+1} | x_t)$ 描述这些状态之间的转换。

逆向过程

在扩散概率模型中，逆向过程的目标是从噪声图像 $x_T$ 重建初始图像 $x_0$ 。这个过程可以通过最大化以下条件概率来实现：

$p(x_0 | x_T) = \frac{p(x_T | x_0) p(x_0)}{p(x_T)}$

逆向过程中的关键挑战是如何对条件概率密度 $p(x_{t-1} | x_t)$ 进行建模。为了解决这个问题，通常会使用神经网络生成器 $G_\theta(x_t, t)$ ，其中 $\theta$ 是生成器的参数， $t$ 是时间步。对于给定的 $x_t$ 和 $t$ ，生成器输出一个概率分布，表示 $x_{t-1}$ 的可能取值。然后，我们可以通过最大化似然进行训练：

$\mathcal{L}(\theta) = \mathbb{E}_{p(x_{t+1} | x_t)}\left[ \log p_\theta(x_t | x_{t+1}, t) \right]$

在训练过程中，我们通过在训练集上对正向过程进行采样，生成一系列中间状态，然后使用这些状态对生成器进行训练。训练完成后，我们可以通过从噪声图像开始，逐步应用生成器来重建初始图像。

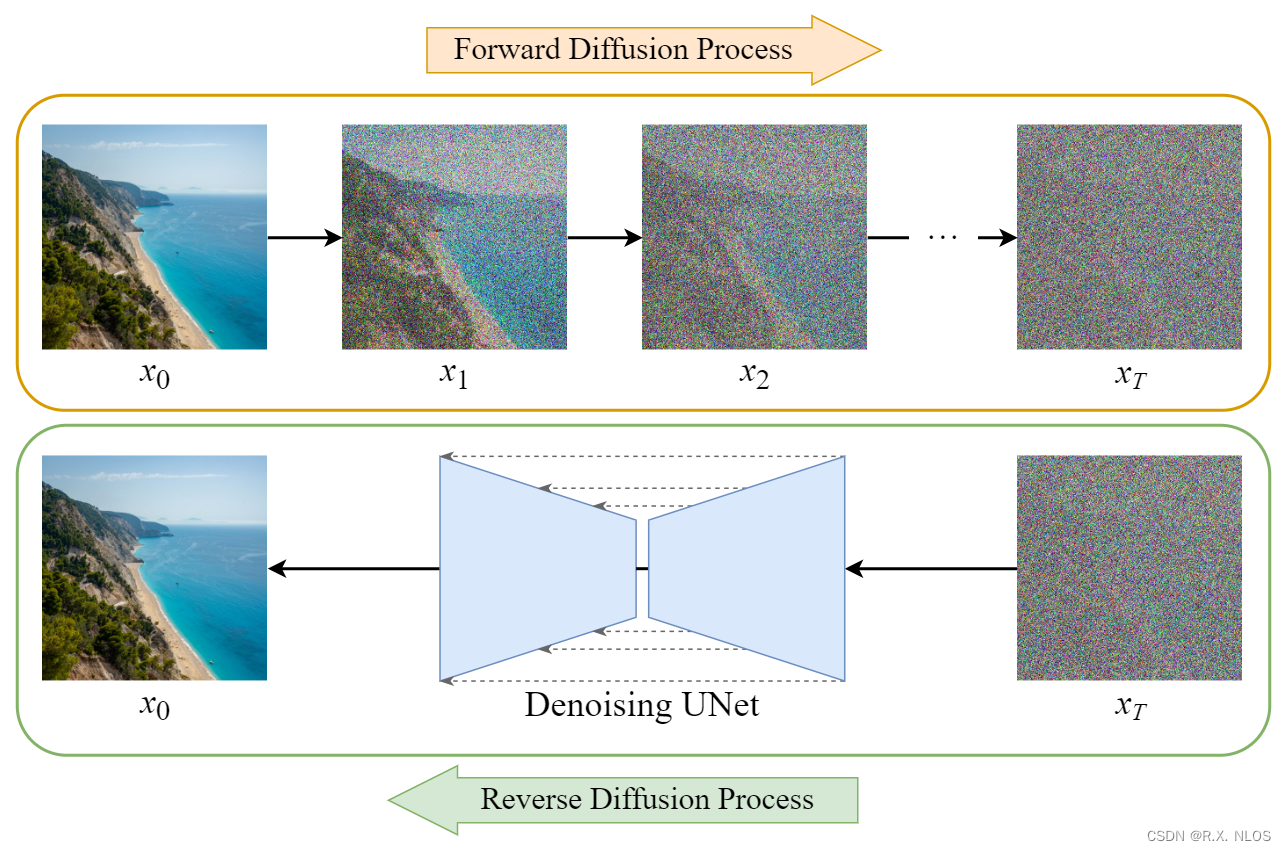
在这里插入图片描述

Diffusion Model Clearly Explained! | by Steins | Medium

研究现状

近年来，基于扩散概率模型的图像生成和重建技术取得了显著进展。以下是一些重要的里程碑：

Denoising Score Matching：首次提出了一种基于扩散概率模型的生成方法，其主要思想是将生成问题转化为一种图像去噪任务。通过学习一个去噪生成器，可以从噪声图像中重建出原始图像。
Denoising Diffusion Implicit Models：提出了一种结合扩散概率模型和隐式生成模型的方法。这种方法允许在生成器的隐式空间中进行采样，从而获得更稳定和高效的图像生成。
Denoising Diffusion Probabilistic Models：进一步完善了扩散概率模型的生成器结构，提出了一种端到端的训练方法。这种方法在图像生成和重建任务上取得了领先的性能，特别是在高分辨率图像生成方面。

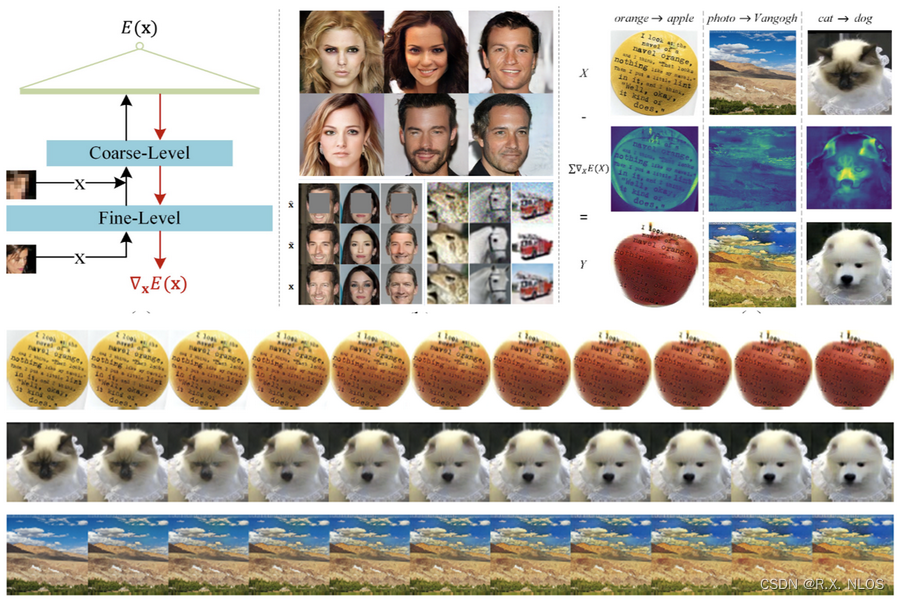
在这里插入图片描述