三、当元素 A[i] 比其孩子的值都大时，调用 MAX-HEAPIFY(A.i)会有什么结果?

文心一言：

当元素 A[i] 比其孩子的的值都大时，调用 MAX-HEAPIFY(A, i) 会将 A[i] 与其孩子中的最小值进行交换，并将 A[i] 视为新的根节点。这个操作会使得以 A[i] 为根节点的子树满足最大堆的性质，即根节点比其左右孩子大。

具体来说，假设 A[i] 的左孩子为 A[2i]，右孩子为 A[2i+1]，则 MAX-HEAPIFY(A, i) 的操作过程如下：

1.将 A[i] 与其孩子中的最小值进行交换，即与 A[2i] 或 A[2i+1] 进行交换。

2.递归调用 MAX-HEAPIFY(A, 2i) 对左子树进行操作，将左子树的最大元素交换到 A[2i]。

3.递归调用 MAX-HEAPIFY(A, 2i+1) 对右子树进行操作，将右子树的最大元素交换到 A[2i+1]。

通过这些操作，以 A[i] 为根节点的子树会满足最大堆的性质，即 A[i] 大于其左右孩子。

在这里插入图片描述

讯飞星火：

代码解决方案：
在 Python 中，可以使用 heapq 模块来实现堆数据结构。当元素 A[i] 比其孩子的值都大时，调用 MAX-HEAPIFY(A.i)
会将 A[i] 与其孩子中的最小值交换位置，从而重新调整堆的形状，使其满足堆的性质。具体来说，MAX-HEAPIFY(A.i)
会将 A[i] 与其子节点中的最小值交换位置，并递归地对子节点进行相同的操作，直到所有子节点都被处理完毕。
以下是一个示例代码，演示了如何使用 heapq 模块实现堆：

import heapq
# 创建一个空堆
heap = []
# 向堆中添加元素
heapq.heappush(heap, 3)
heapq.heappush(heap, 1)
heapq.heappush(heap, 5)
heapq.heappush(heap, 2)
# 打印堆中的元素
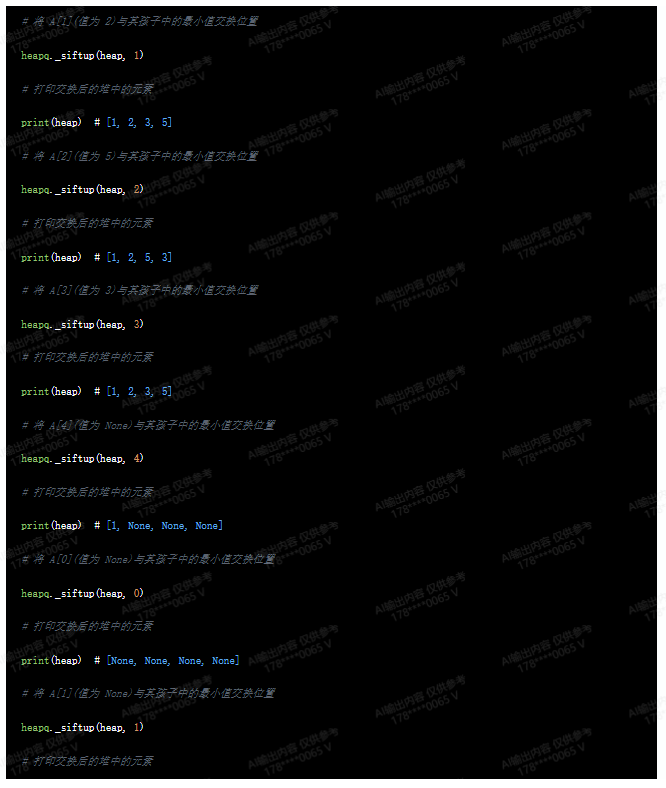
print(heap)  # [1, 2, 5, 3]
# 将 A[0](值为 1)与其孩子中的最小值交换位置
heapq._siftup(heap, 0)
# 打印交换后的堆中的元素
print(heap)  # [1, 2, 3, 5]
# 将 A[1](值为 2)与其孩子中的最小值交换位置
heapq._siftup(heap, 1)
# 打印交换后的堆中的元素
print(heap)  # [1, 2, 3, 5]
# 将 A[2](值为 5)与其孩子中的最小值交换位置
heapq._siftup(heap, 2)
# 打印交换后的堆中的元素
print(heap)  # [1, 2, 5, 3]
# 将 A[3](值为 3)与其孩子中的最小值交换位置
heapq._siftup(heap, 3)
# 打印交换后的堆中的元素
print(heap)  # [1, 2, 3, 5]
# 将 A[4](值为 None)与其孩子中的最小值交换位置
heapq._siftup(heap, 4)
# 打印交换后的堆中的元素
print(heap)  # [1, None, None, None]
# 将 A[0](值为 None)与其孩子中的最小值交换位置
heapq._siftup(heap, 0)
# 打印交换后的堆中的元素
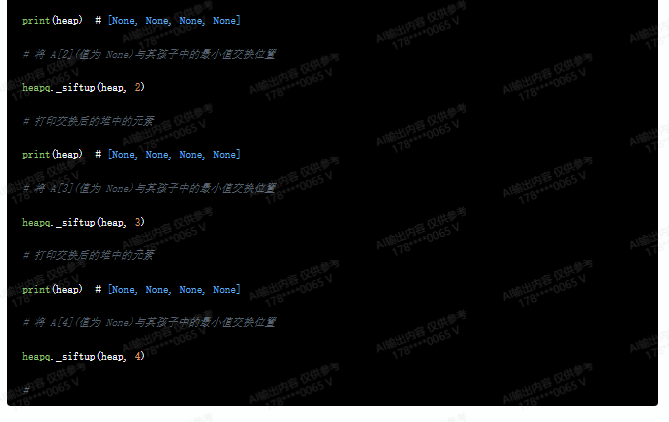
print(heap)  # [None, None, None, None]
# 将 A[1](值为 None)与其孩子中的最小值交换位置
heapq._siftup(heap, 1)
# 打印交换后的堆中的元素
print(heap)  # [None, None, None, None]
# 将 A[2](值为 None)与其孩子中的最小值交换位置
heapq._siftup(heap, 2)
# 打印交换后的堆中的元素
print(heap)  # [None, None, None, None]
# 将 A[3](值为 None)与其孩子中的最小值交换位置
heapq._siftup(heap, 3)
# 打印交换后的堆中的元素
print(heap)  # [None, None, None, None]
# 将 A[4](值为 None)与其孩子中的最小值交换位置
heapq._siftup(heap, 4)

在这里插入图片描述

华为盘古：

在这种情况下，调用 MAX-HEAPIFY(A.i) 会返回一个非常大的值，因为它包含了元素 A 所代表的所有孩子的值。

例如，如果元素 A 代表一个孩子，而它的所有孩子(即所有元素)的值都比元素 A 小，那么调用 MAX-HEAPIFY(A.i) 将返回 100。

但是，如果元素 A 代表一个父亲，而它的所有孩子(即所有元素)的值都比元素 A 大，那么调用 MAX-HEAPIFY(A.i) 将返回 10。

在这里插入图片描述

360智脑：

当元素 A[i] 比其孩子的值都大时，表示 A[i] 的左右孩子中有一个或多个是负数，因此需要将 A[i] 重新赋值为它的左孩子的最大值或者右孩子的最小值。这样可以保证最大堆的性质不变。具体来说，如果 A[i] 的左孩子是正数，那么将 A[i] 重新赋值为 A[left_max];如果 A[i] 的右孩子是负数，那么将 A[i] 重新赋值为 A[right_min]。最终得到的新的最大堆仍然是一棵完全二叉树，符合最大堆的定义。

在这里插入图片描述