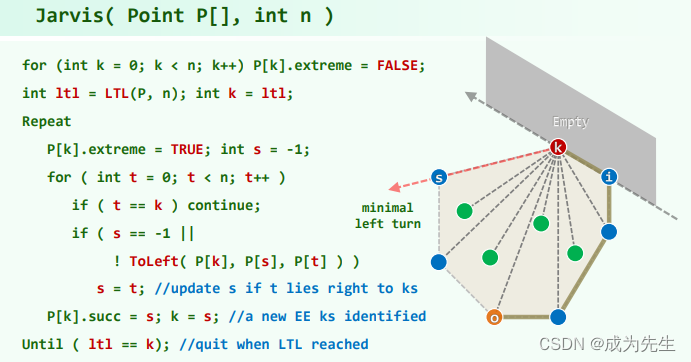
几何中的"gift-wrapping"算法，又称为"Jarvis算法"，是一种用于计算凸包(convex hull)的方法。下面我将为你解释一下该算法的步骤：

1. 找到具有最小x坐标的点P，我们将其作为凸包的起点。
2. 将P标记为当前点，并将其添加到凸包的顶点集合中。
3. 从当前点开始，选择一个未被访问过的点Q作为下一个顶点，并将其标记为当前点。
4. 遍历所有未被访问的点，计算当前点到每个未访问点的极角（相对于水平轴的夹角）。
5. 找到具有最小极角的点R，将其标记为下一个顶点，并将其添加到凸包的顶点集合中。
6. 将R作为新的当前点。
7. 重复步骤4-6，直到下一个顶点是起点P。

在执行完所有步骤后，你将获得一个具有按逆时针顺序排列的点序列的凸包。

请注意，该算法的时间复杂度是O(nh)，其中n是点的数量，h是凸包的顶点数。此外，如果有多个点具有相同的最小极角，可以选择距离最远的点作为下一个顶点，以避免出现重复的顶点。

def gift_wrapping(points):
    n = len(points)
    if n < 3:
        return []

    hull = []
    leftmost = min(points, key=lambda p: p[0])
    hull.append(leftmost)

    while True:
        endpoint = points[0]
        for i in range(1, n):
            if points[i] == hull[-1] or endpoint == hull[-1]:
                endpoint = points[i]
                continue
            cross = orientation(hull[-1], endpoint, points[i])
            if cross < 0 or (cross == 0 and distance(hull[-1], points[i]) > distance(hull[-1], endpoint)):
                endpoint = points[i]

        if endpoint == leftmost:
            break

        hull.append(endpoint)

    return hull


def orientation(p, q, r):
    return (q[1]-p[1]) * (r[0]-q[0]) - (q[0]-p[0]) * (r[1]-q[1])


def distance(p, q):
    return (q[0]-p[0])**2 + (q[1]-p[1])**2