【C语言】手把手带你解决青蛙跳台阶问题

news2024/11/16 1:17:50

在这里插入图片描述

君兮_的个人主页

勤时当勉励岁月不待人

C/C++ 游戏开发

Hello,这里是君兮_，今天更新的是经典递归问题——青蛙跳台阶，在所有有关递归的问题中，青蛙跳台阶是最广为人知的问题之一，可以说，如果你能真正弄懂青蛙跳台阶问题，你的递归也一定不会太差，今天就来带大家深度解析一下青蛙跳台阶问题。

青蛙跳台阶

青蛙跳台阶问题的详细描述
具体解决青蛙跳台阶问题
- 青蛙跳台阶问题解题思路分析
- - 思路总结
- 在C语言中实现青蛙跳台阶
- - 问题进阶：
  - 思路分析
总结

青蛙跳台阶问题的详细描述

一只青蛙一次可以跳上1级台阶，也可以跳上2级台阶。求该青蛙跳上一个n级的台阶总共有多上种跳法。

具体解决青蛙跳台阶问题

青蛙跳台阶问题解题思路分析

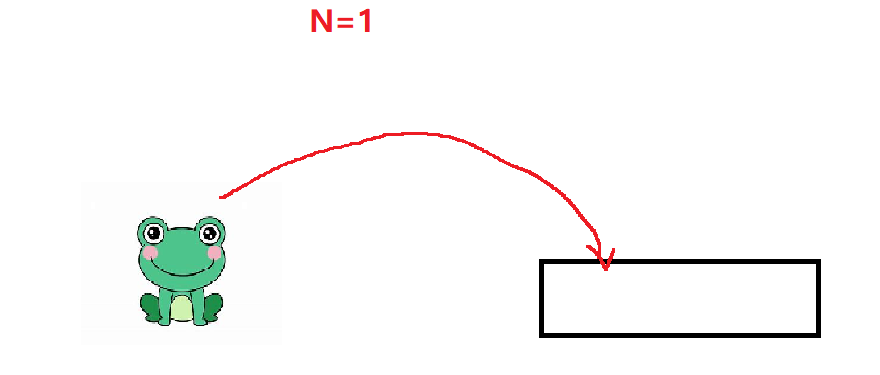
当N=1时，那么青蛙就只有一种跳法。
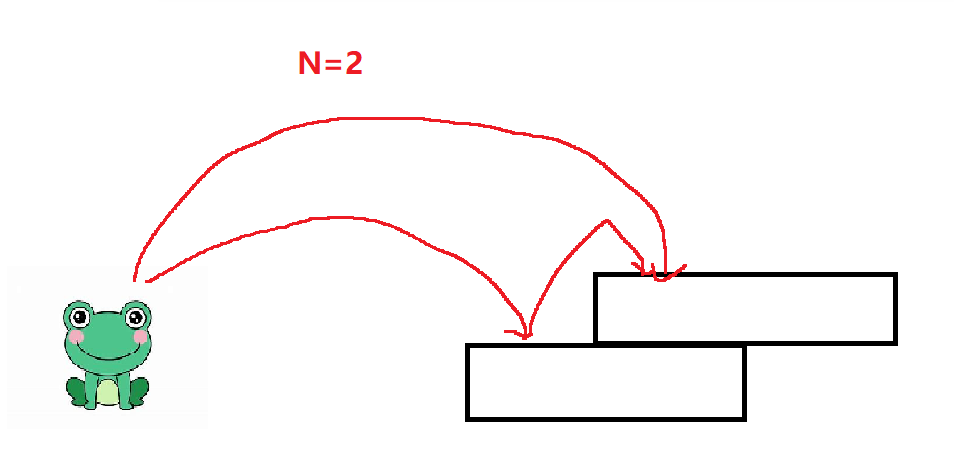
当N=2时，青蛙可以跳两次一层台阶也可以跳一次二层台阶，有两种跳法。
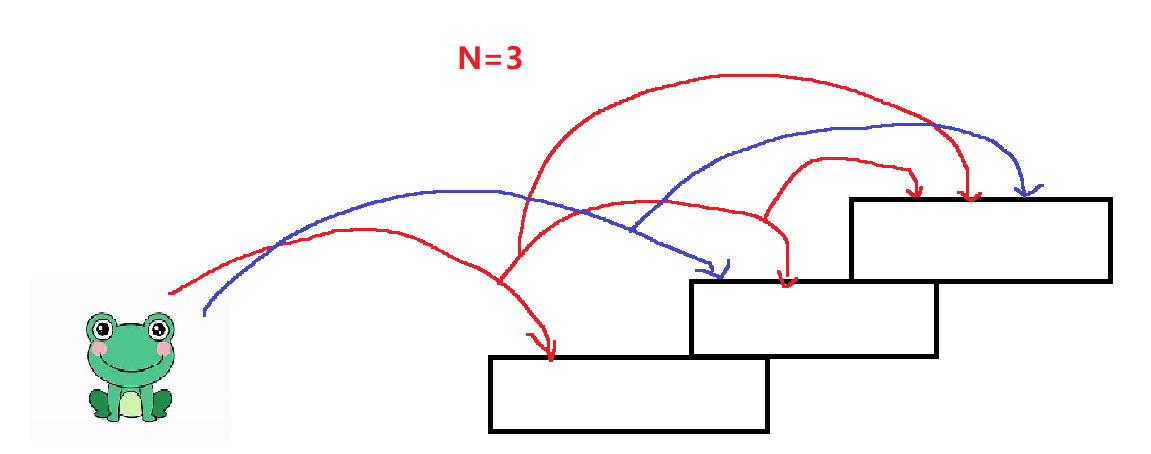
当N=3时，青蛙可以先跳一次一层台阶，那么还需要跳两层台阶，那它此时就是N=2时的跳法，有两种跳法。
当青蛙跳一次二层台阶时，此时只需要跳一层台阶，那么它就是N=1时的跳法。
此时它的跳法就等于（N=1）+（N=2）种跳法。
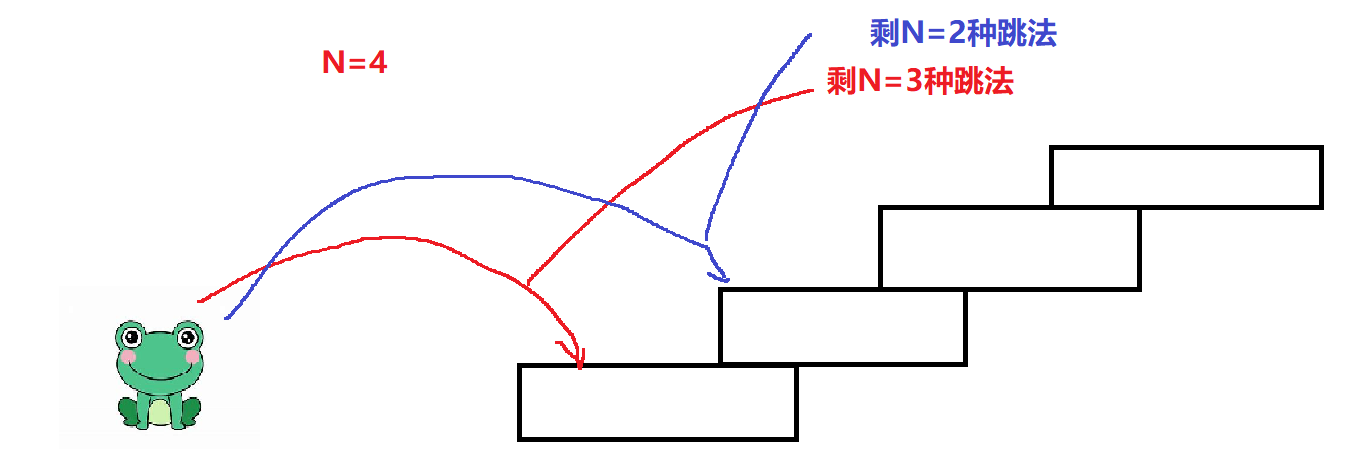
当N=4时，青蛙跳一次一层台阶时，还需要跳三层台阶，那它此时剩下的跳法就等于N=3时的跳法，即有三种跳法。
青蛙跳一次二层台阶时，还剩二层台阶需要跳，那它此时剩下的跳法就是N=2时的跳法，则有两种跳法。
那么此时它的跳法就等于（N=2）+（N=3）种跳法。

思路总结

那么，不难看出青蛙跳台阶的规律，当N>2时，此时的跳法数就等于前面两个青蛙跳台阶跳法数之和

在C语言中实现青蛙跳台阶

代码实现

#include<stdio.h>
int Jump(int n)
{
	if (n == 1)
	{
		return 1;//当只有一层台阶时直接返回1
	}
	 if (n == 2)
	{
		return 2;//当只有2层台阶时就返回2
	}
	 if (n > 2)
	 {
		 return Jump(n - 1) + Jump(n - 2);
	 }//当n>2时，利用递归进行返回
}
int main()
{
	int n = 0;
	scanf("%d", &n);
	int num = Jump(n);
	printf("%d\n", num);
	return 0;
}

问题进阶：

一只青蛙一次可以跳上1级台阶，也可以跳上2级台阶，也可以跳上3级台阶。求该青蛙跳上一个n级的台阶总共有多上种跳法。

思路分析

首先，当N=1时，那么青蛙就有一种跳法。
当N=2时，青蛙可以跳两次一层台阶也可以跳一次二层台阶，有两种跳法
当N=3时，当青蛙首先跳一次一层台阶时，那么还需要跳两层台阶，那它此时就是N=2时的跳法，即有两种跳法。
当青蛙跳一次二层台阶时，此时只需要再跳一层台阶，那么它此时就是N=1时的跳法，即有一种跳法。
最后就是青蛙直接跳三层台阶，只有一种跳法。那么它的跳法总数就是（N=1）+（N=2）+1=4种跳法。
当N=4时，青蛙跳一次一层台阶时，还剩三层台阶需要跳，那它此时就是N=3时的跳法，即有四种跳法。
青蛙跳一次二层台阶时，还剩二层台阶需要跳，那它此时就是N=2时的跳法，则有两种跳法。那么它的跳法总数即为（N=2）+（N=3）=6种跳法。
规律总结
当N>3时，本质上就是前面两个跳法相加就得到此时青蛙跳台阶方法的总数。
代码演示如下：

#include<stdio.h>
int Jump(int n)
{
	if (n == 1)
	{
		return 1;
	}
	if (n == 2)
	{
		return 2;
	}
	if (n == 3)
	{
		return 3;
	}
	if (n > 3)
	{
		return Jump(n - 1) + Jump(n - 2)+Jump(n-3);
	}
}
 
int main()
{
	int n = 0;
	scanf("%d", &n);
	int num = Jump(n);
	printf("%d\n", num);
	return 0;
}