b站刘二大人《PyTorch深度学习实践》课程第四讲反向传播笔记与代码:https://www.bilibili.com/video/BV1Y7411d7Ys?p=4&vd_source=b17f113d28933824d753a0915d5e3a90

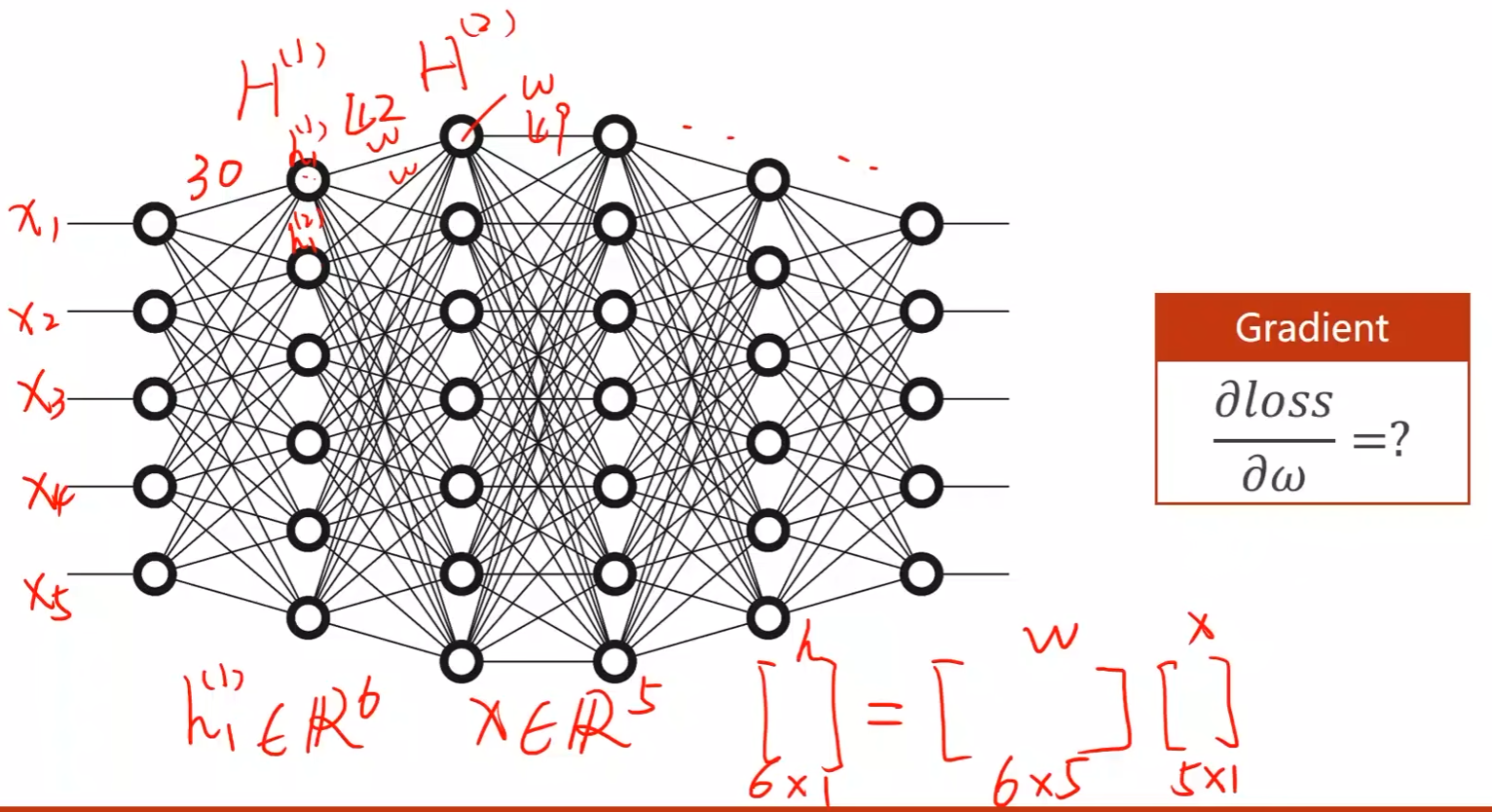
对于上述简单的模型可以用解析式来做,但是对于复杂模型而言,如下图每个圆圈中都有一个权重,诶个写解析式求解极其麻烦,几乎不可能
计算图Computational Graph
-
面对复杂网络,将其看作一个图,在图上来传播梯度,最终根据链式法则将其求出
-
以一个两层神经网络为例
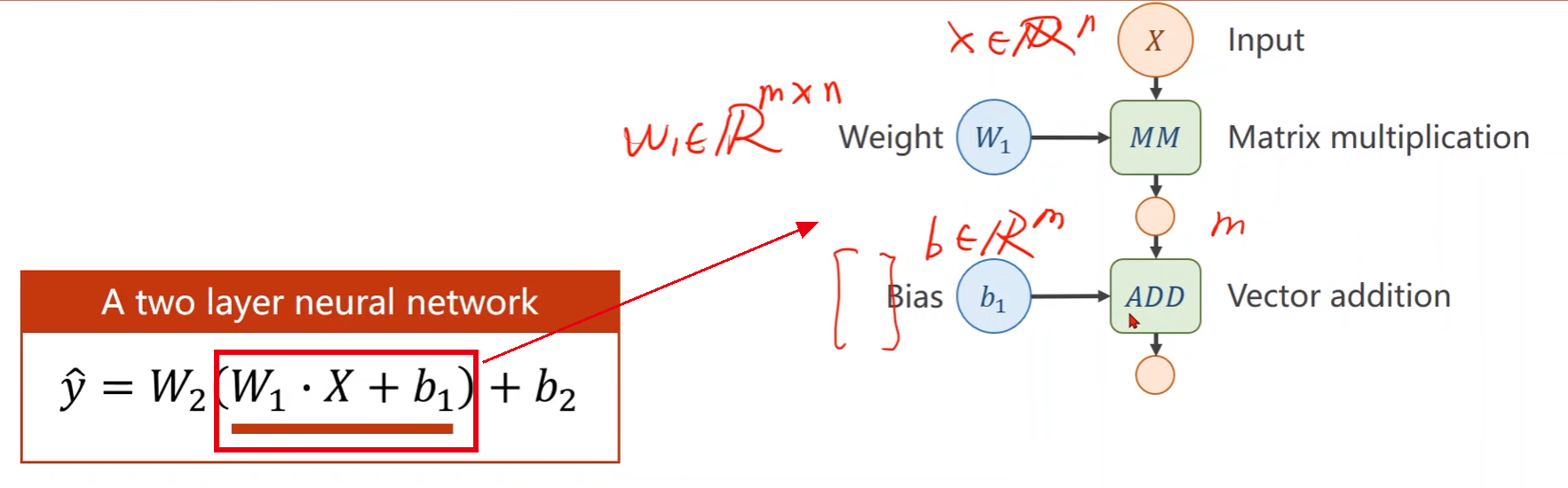
-
MM:Matrix Multiplication,矩阵乘法;ADD:向量加法
-
其中绿色模块就是计算模块
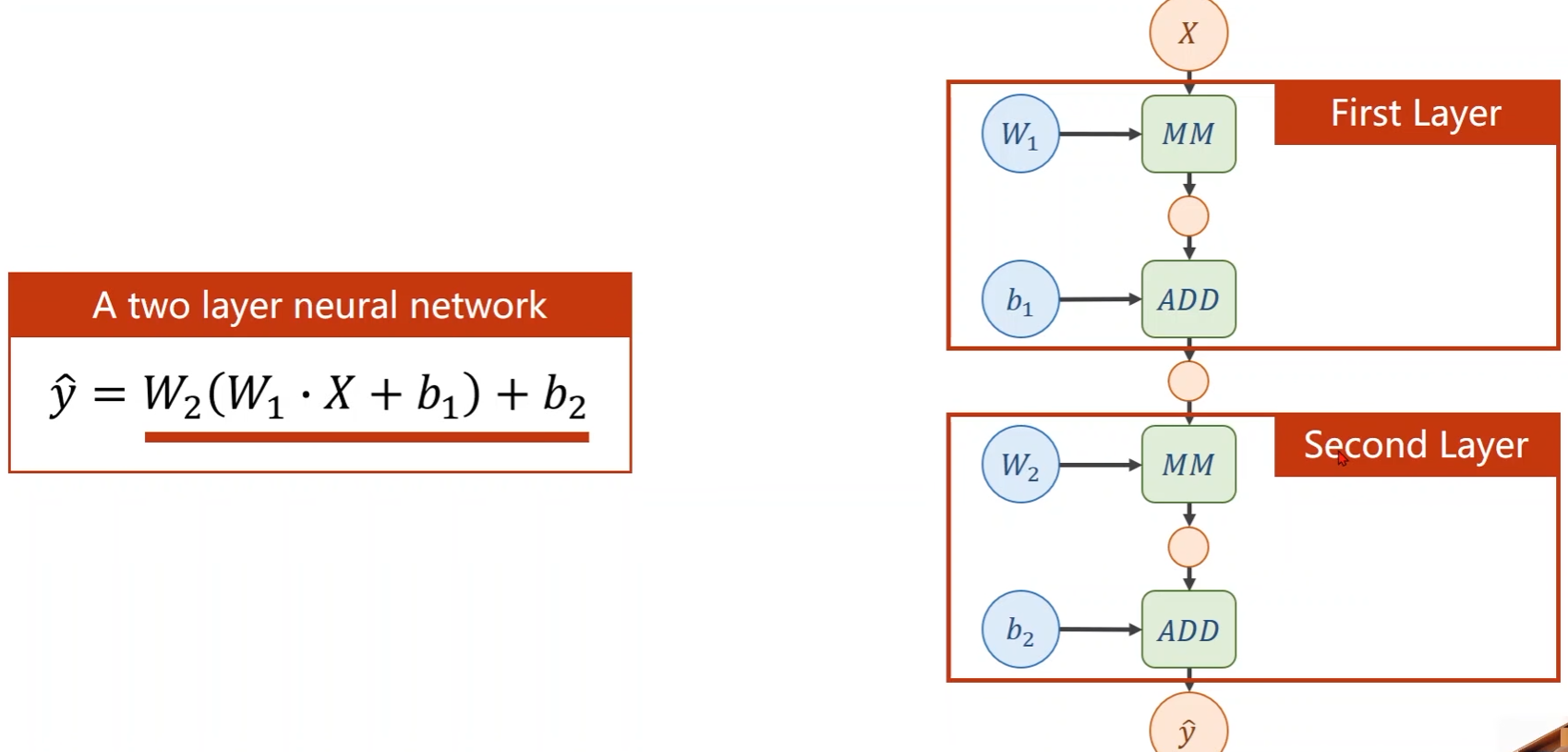
-
注意:上面给出的神经网络 y ^ \hat{y} y^可以对其进行展开,展开之后就会发现如果就这样一直线性展开,不管有多少层,最终得到的都能统一为一层,这样的话层数多和层数少都没区别
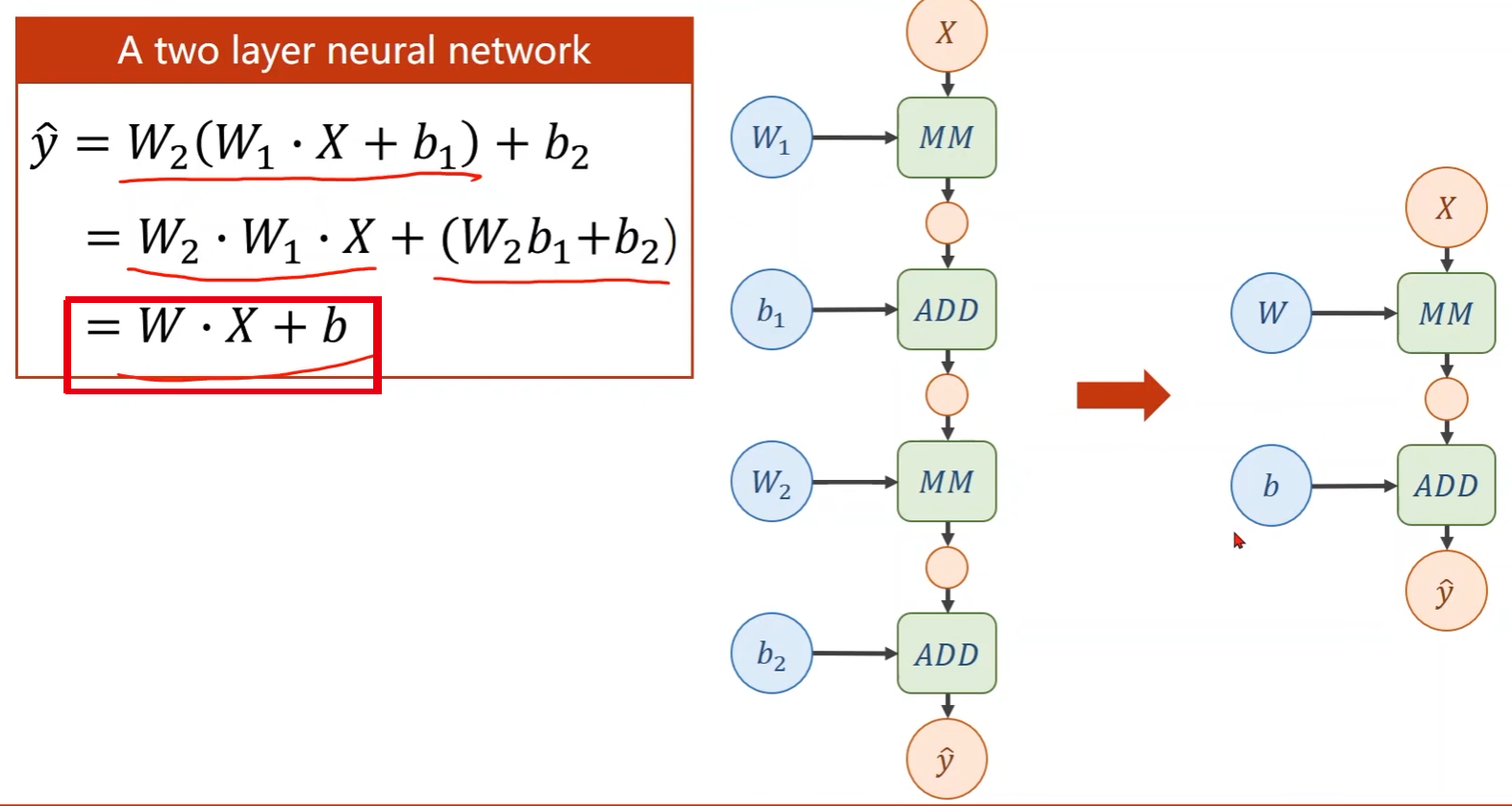
-
解决方法:对每一层的输出加一个非线性函数,使其不能化简
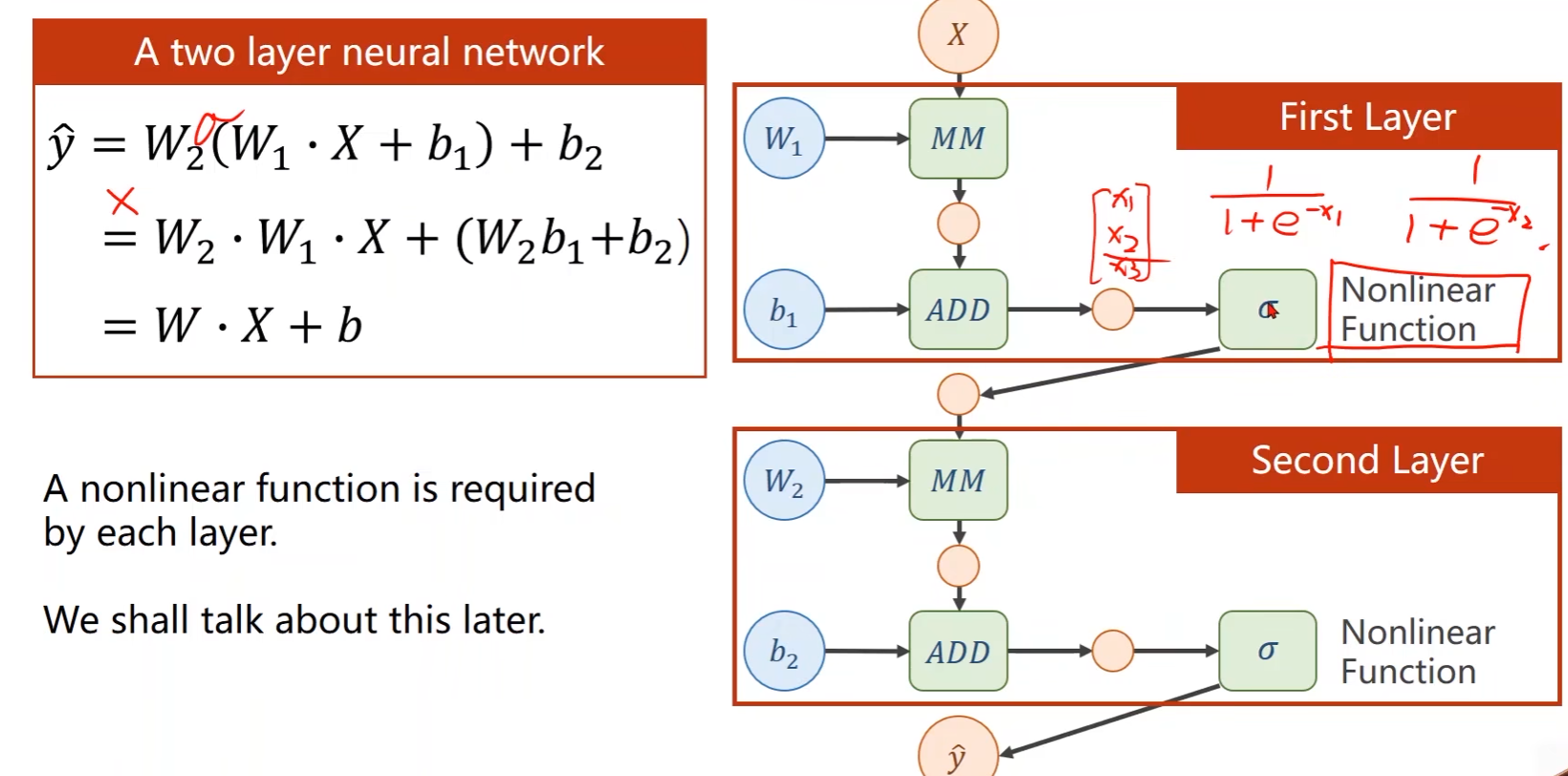
-
链式法则(Chain Rule):
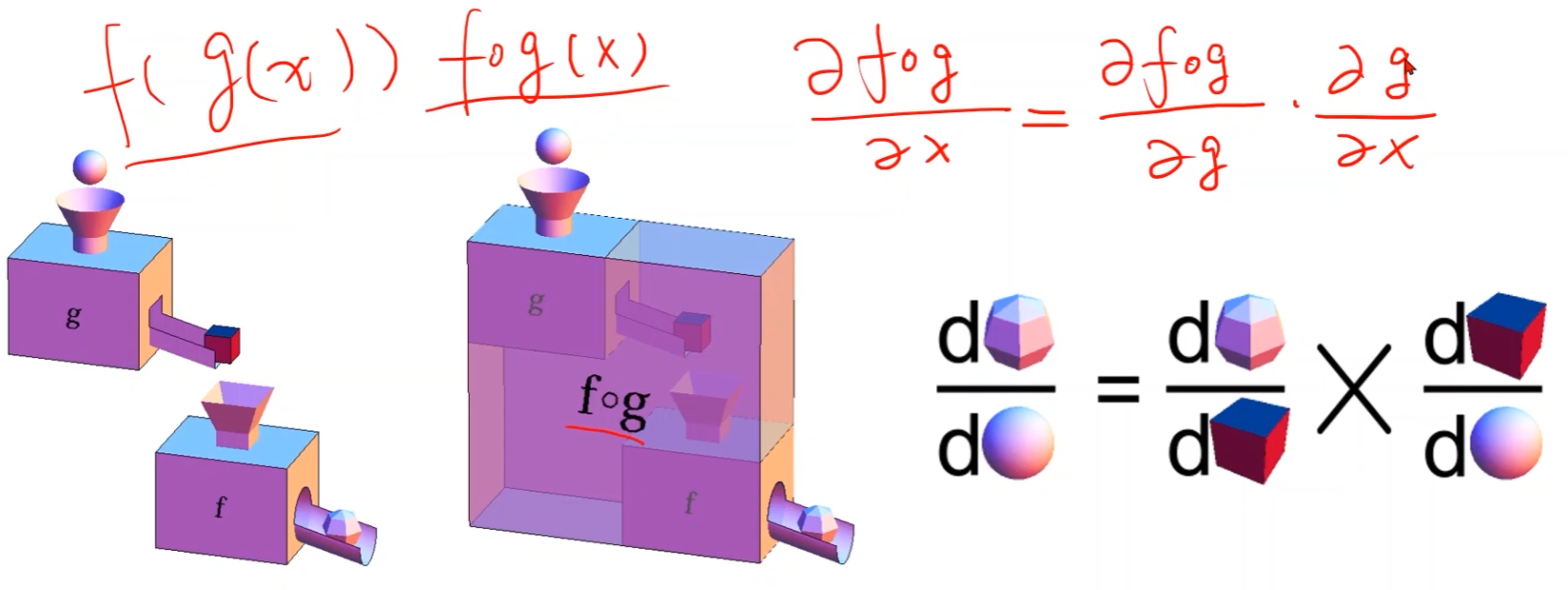
步骤:
-
Create Computational Graph(Forward)
- 前馈运算
- 从输入 x x x沿着边向最终的loss计算
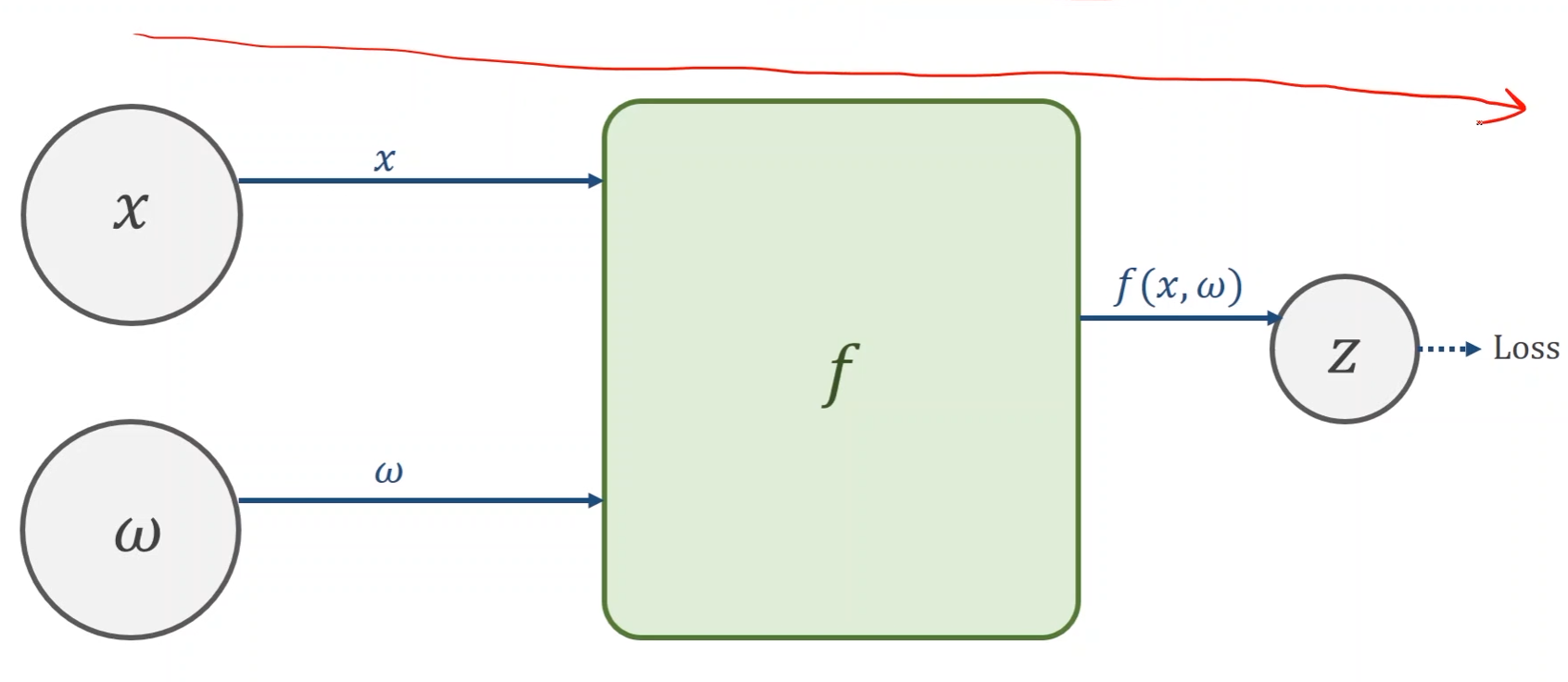
- 前馈运算
-
Local Gradient
- 函数 f f f是用于计算输出 Z Z Z关于输入 x x x和权重 w w w的导数
- Z = f ( x , w ) Z = f(x,w) Z=f(x,w)
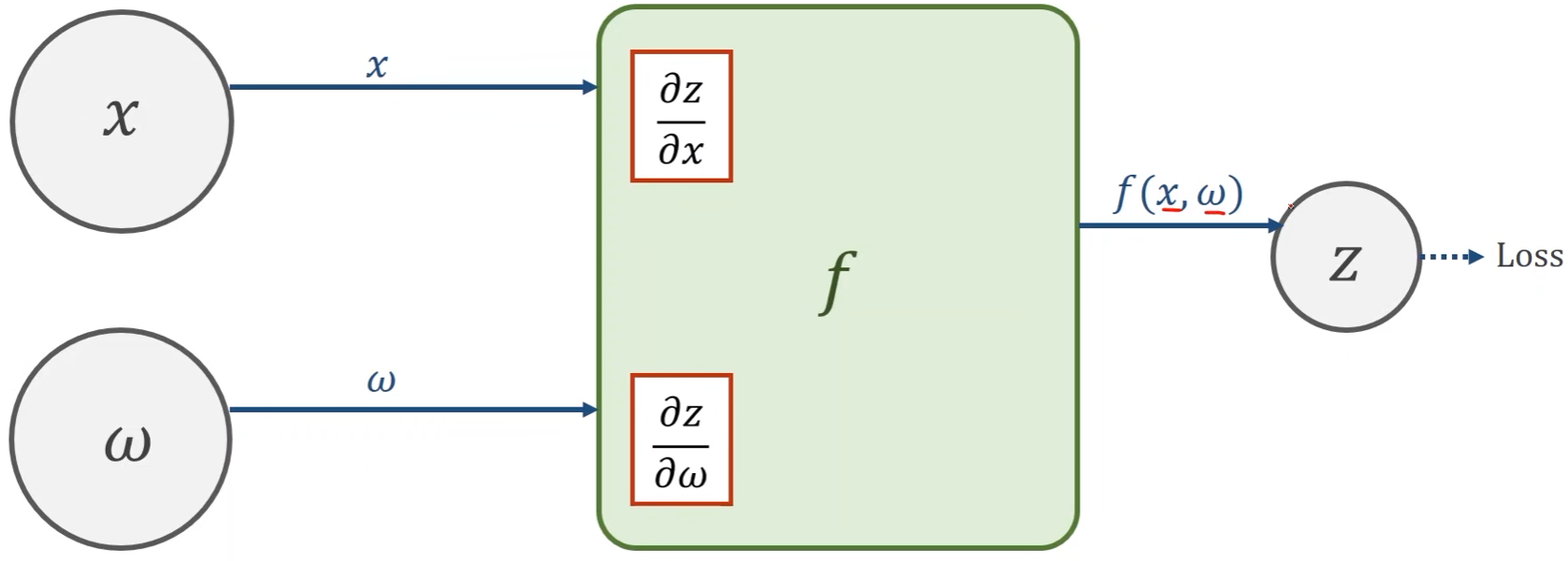
-
Given gradient from successive node
- 对于输出结果
Z
Z
Z而言,首先要拿到最终的损失函数Loss对它的偏导
∂
L
∂
z
\frac{\partial L}{\partial z}
∂z∂L
- 该偏导是从Loss传回来的。先是从最初的输入 x x x通过前馈一步一步计算到最终的损失函数Loss(前馈过程),然后再从Loss开头一步一步往回算(反馈过程)
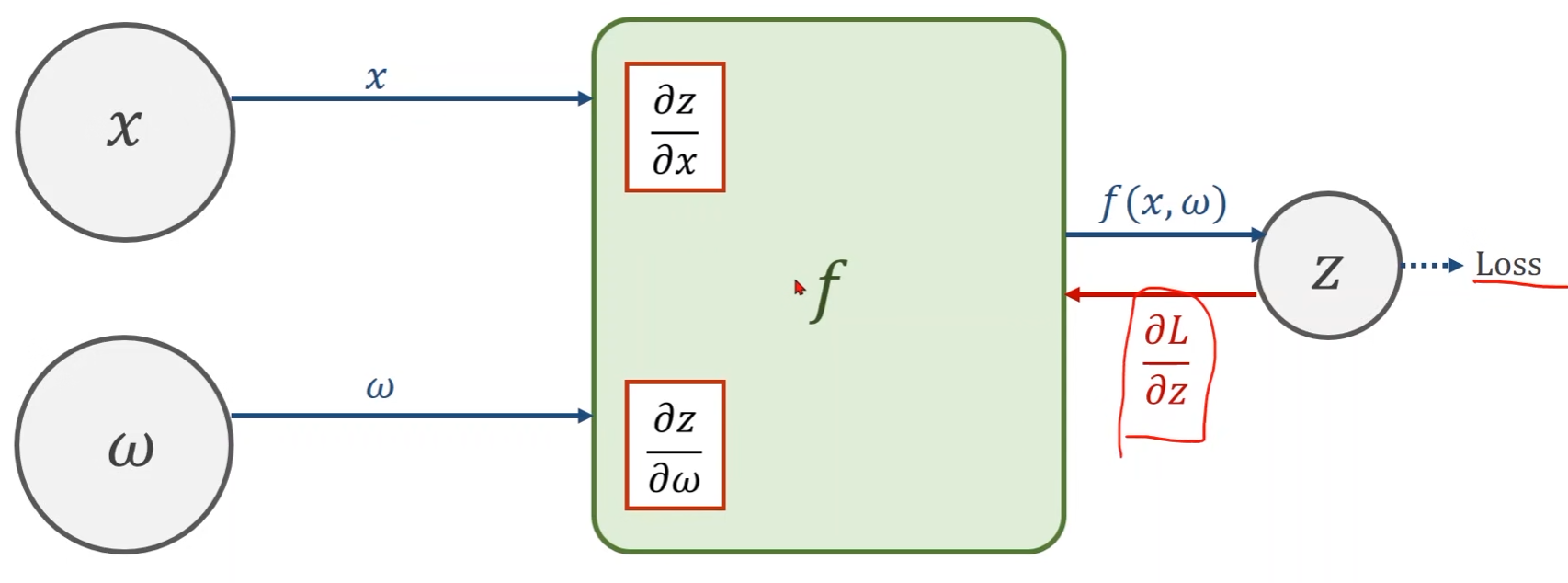
- 对于输出结果
Z
Z
Z而言,首先要拿到最终的损失函数Loss对它的偏导
∂
L
∂
z
\frac{\partial L}{\partial z}
∂z∂L
-
**Use chain rule to compute the gradient (Backward) **
- 拿到 ∂ L ∂ z \frac{\partial L}{\partial z} ∂z∂L后,经过计算 f f f,我们的目标是得到Loss关于输入 x x x和权重 w w w的偏导,这一计算过程需使用上链式法则
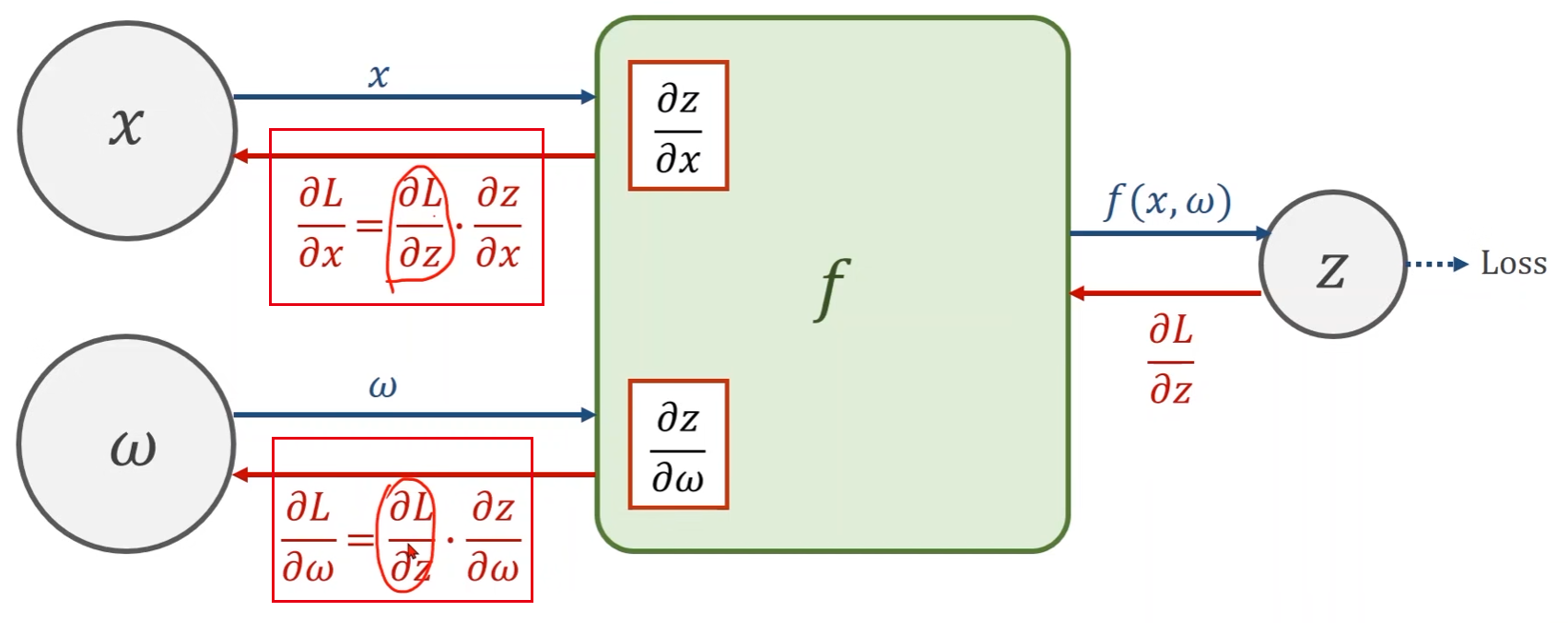
实例一:
-
f
=
x
⋅
w
f = x · w
f=x⋅w,令
x
=
2
,
w
=
3
x = 2, w = 3
x=2,w=3
- 输出Z关于输入 x x x的偏导: ∂ Z ∂ x = ∂ x ⋅ w ∂ x = w \frac{\partial Z}{\partial x} = \frac{\partial x·w}{\partial x} = w ∂x∂Z=∂x∂x⋅w=w
- 输出Z关于权重 w w w的偏导: ∂ Z ∂ w = ∂ x ⋅ w ∂ w = x \frac{\partial Z}{\partial w} = \frac{\partial x·w}{\partial w} = x ∂w∂Z=∂w∂x⋅w=x
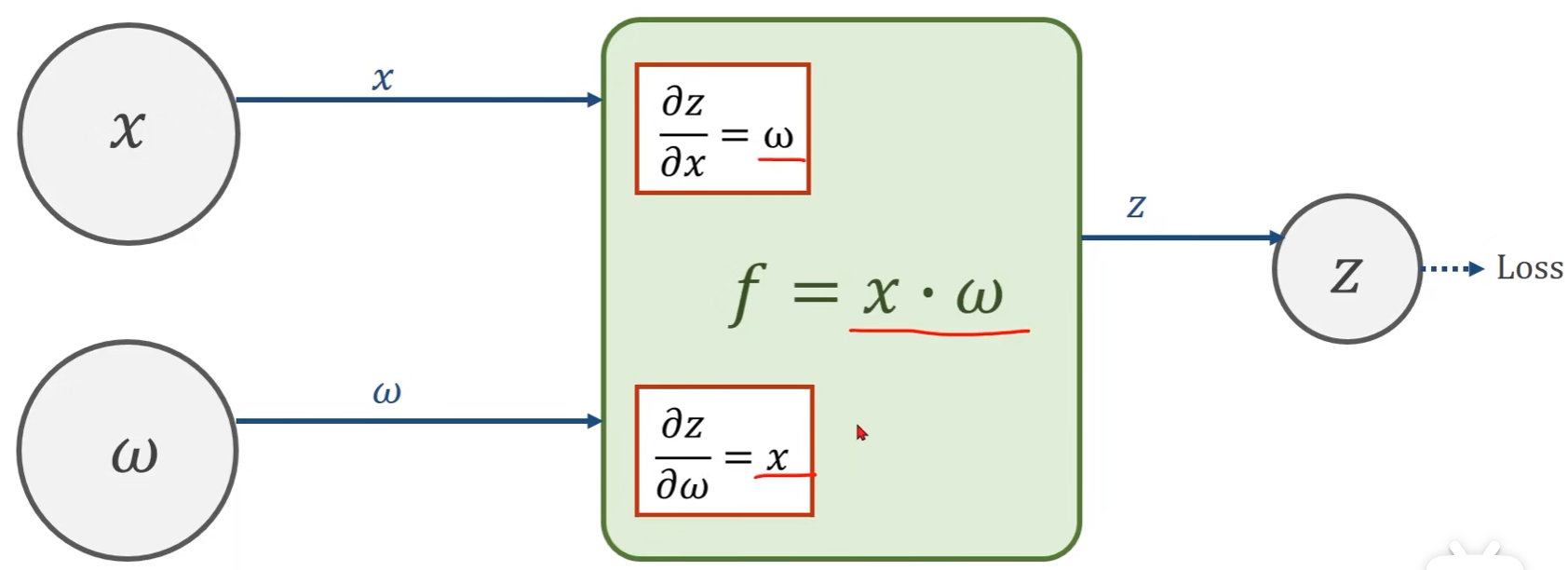
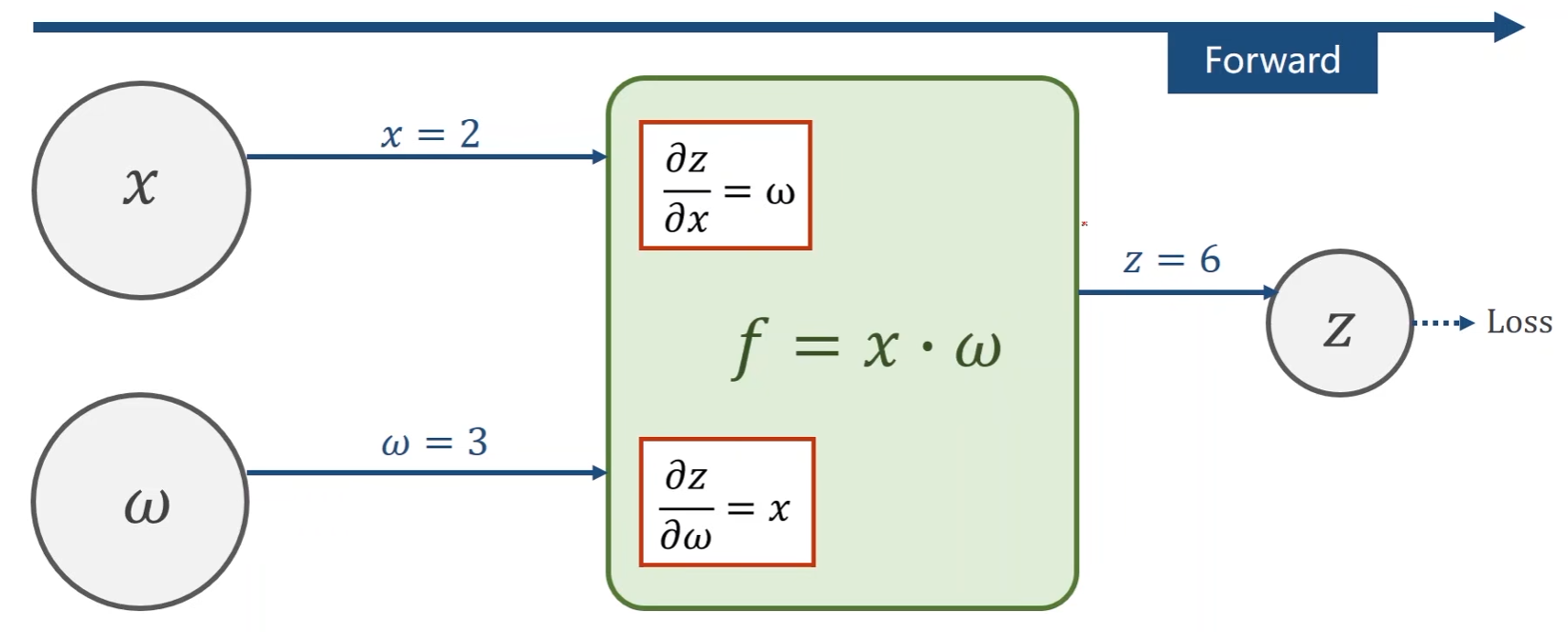
前馈过程:
- 由 x x x和 w w w计算得到 z z z
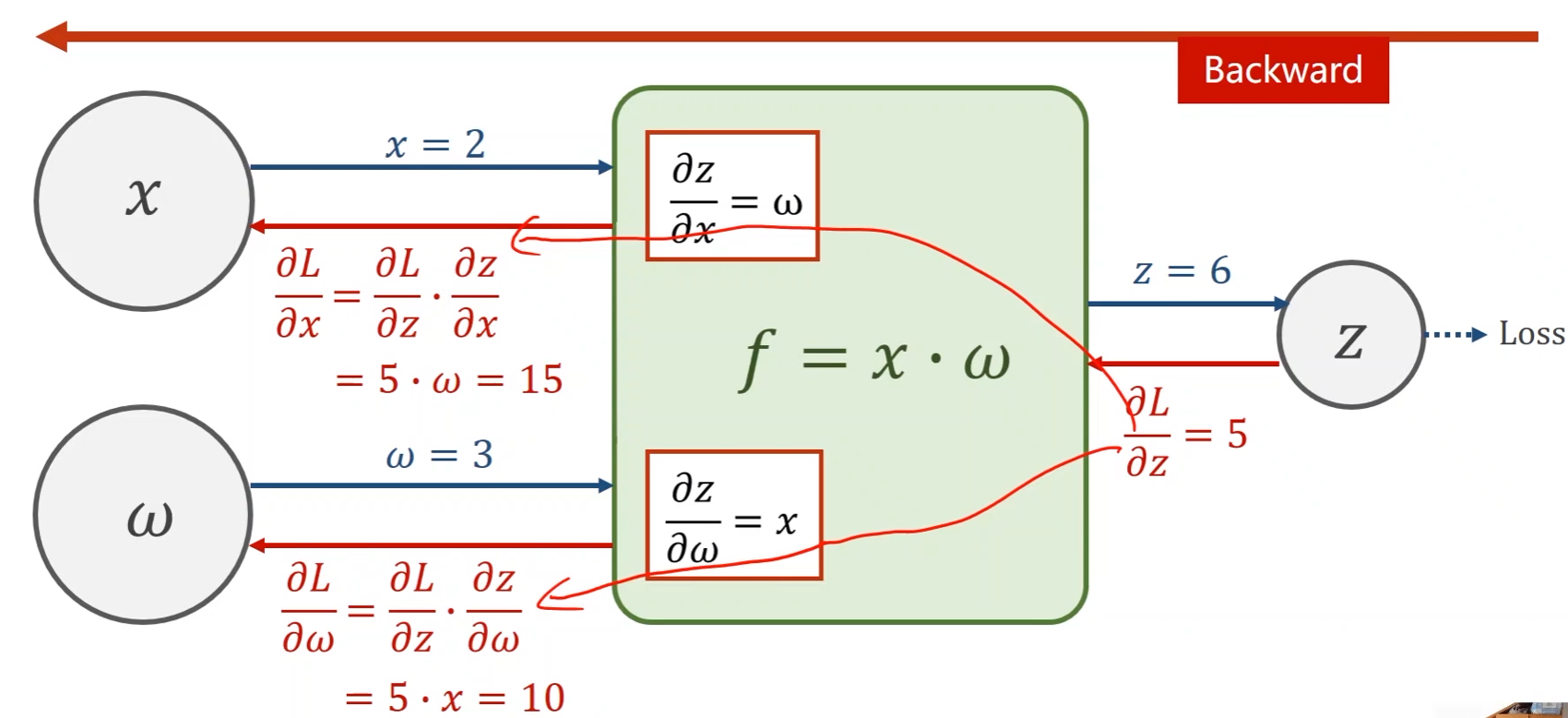
反馈过程:
- 假设由前一步得到最终的损失函数Loss对 Z Z Z的偏导为5
线性模型 y ^ = x ∗ w \hat{y} = x * w y^=x∗w的计算图
-
模型计算图
- 假设输入 x = 1 x = 1 x=1,权重 w = 1 w = 1 w=1,那么 y ^ = x ∗ w = 1 \hat{y} = x * w = 1 y^=x∗w=1
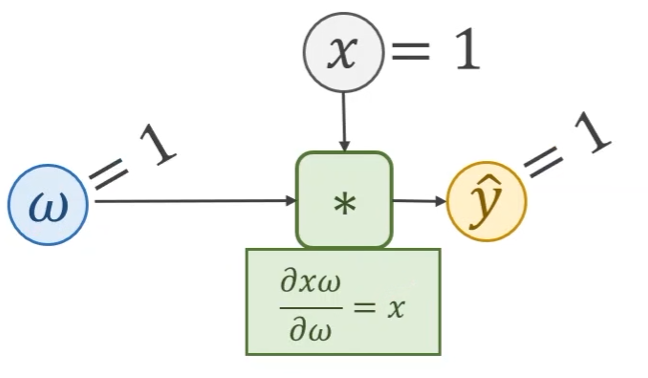
-
loss计算图, l o s s = ( y ^ − y ) 2 = ( x ⋅ w − y ) 2 loss = (\hat{y} - y)^2 = (x·w - y)^2 loss=(y^−y)2=(x⋅w−y)2
- 将 ( y ^ − y ) (\hat{y} - y) (y^−y)称为残差项(residual),记为 r = y ^ − y r = \hat{y} - y r=y^−y
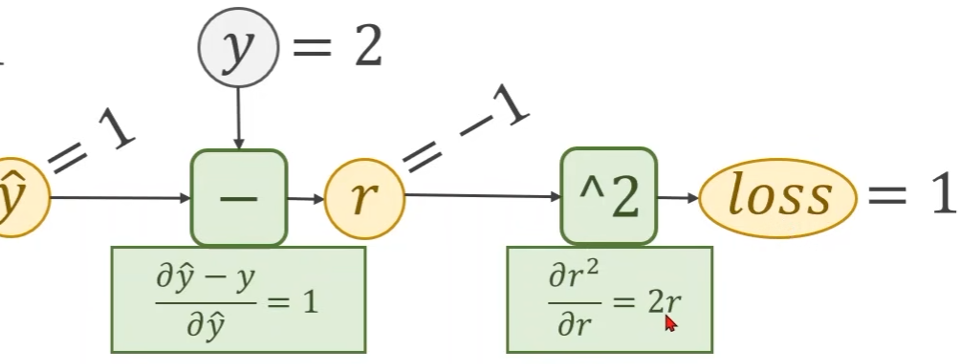
- 假设 y = 2 y = 2 y=2,那么残差项 r = y ^ − y = − 1 r = \hat{y} - y = -1 r=y^−y=−1,残差对 y ^ \hat{y} y^的导数 ∂ y ^ − y ∂ y ^ = 1 \frac{\partial \hat{y} - y}{\partial \hat{y}} = 1 ∂y^∂y^−y=1
上述即为前馈过程:
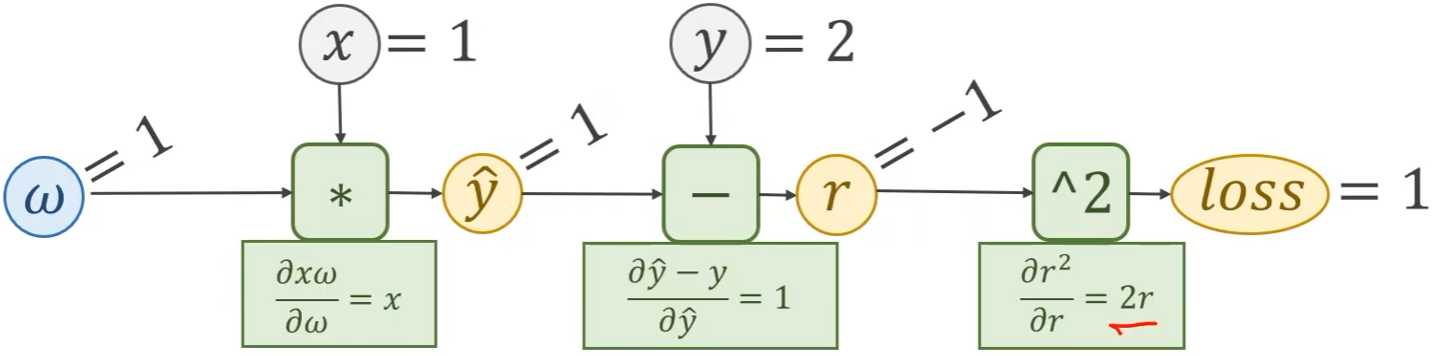
- 不仅能计算出到下一步的输出值,还能够计算出局部的梯度
接下去就是反馈过程:
-
首先求损失函数loss关于残差项 r r r的偏导, l o s s = r 2 loss = r^2 loss=r2
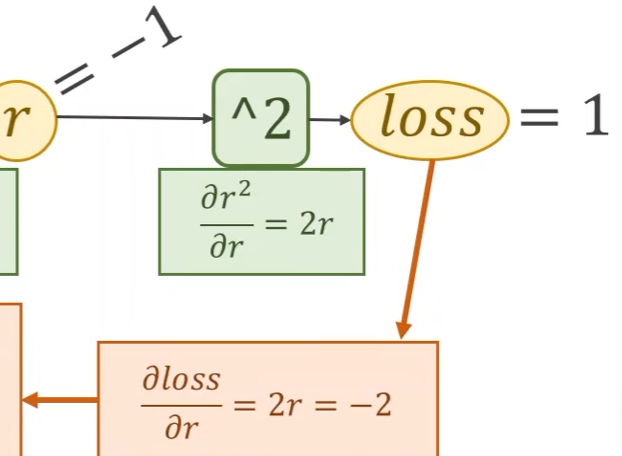
-
再计算损失关于 y ^ \hat{y} y^的偏导
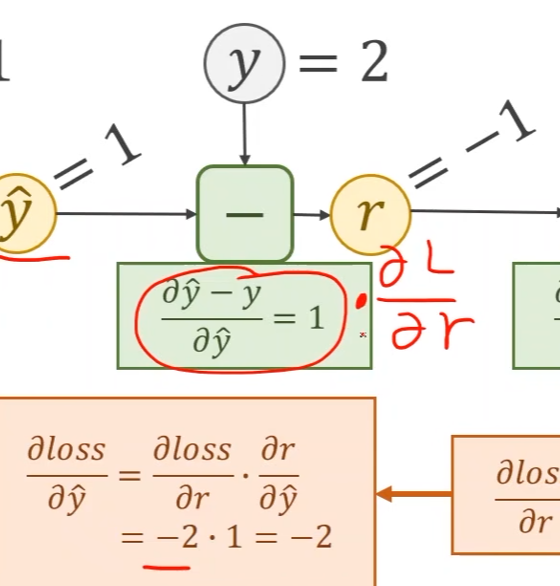
-
最终得到损失关于权重 w w w的偏导
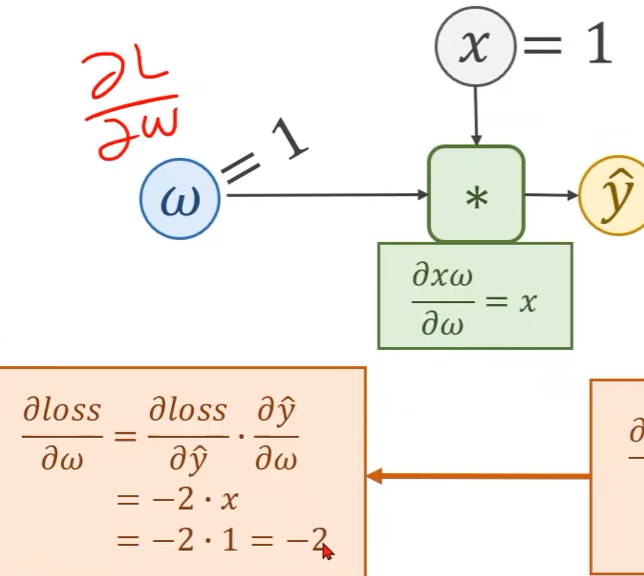
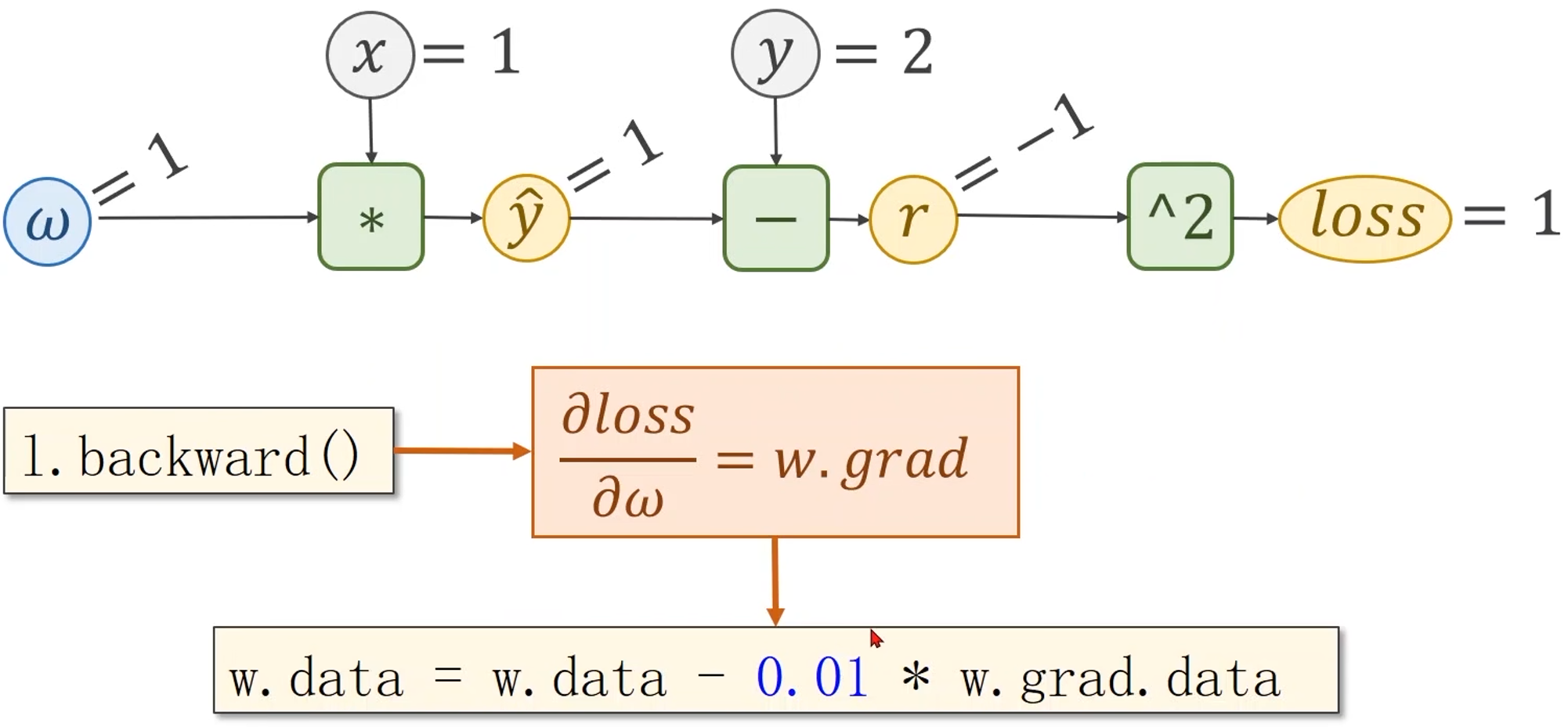
完整的计算图:
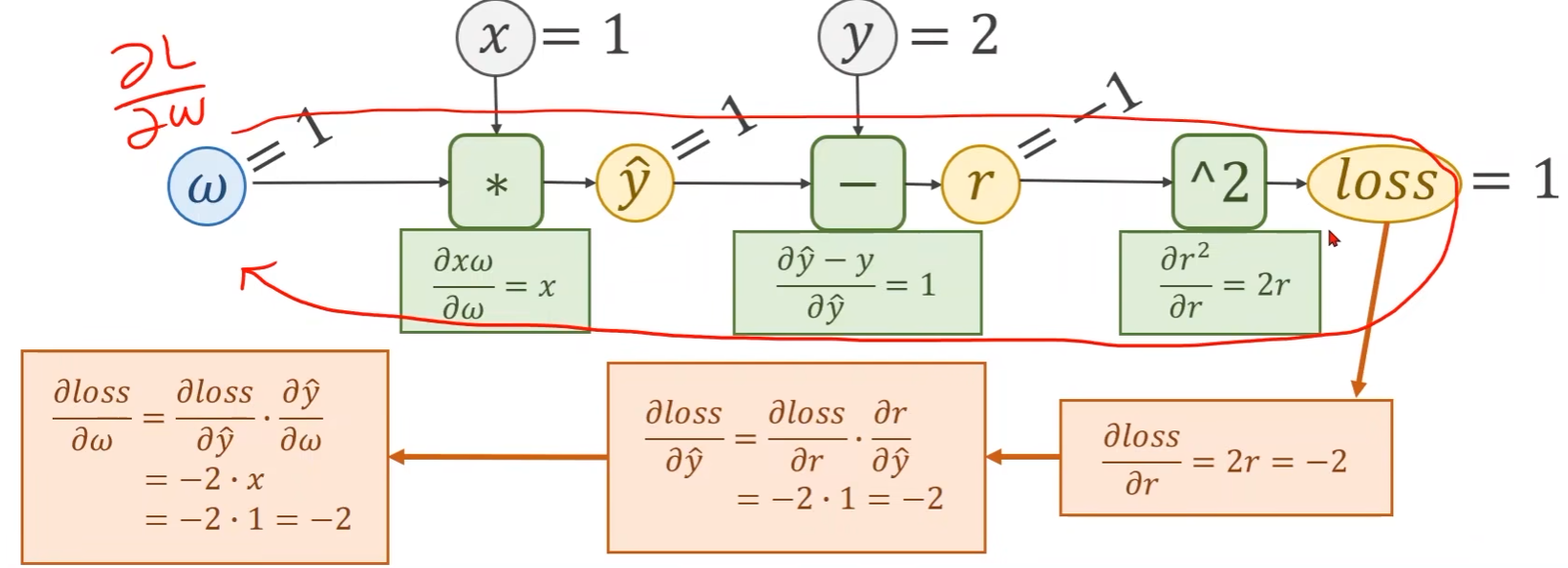
PyTorch中如何实现前馈和反馈计算???
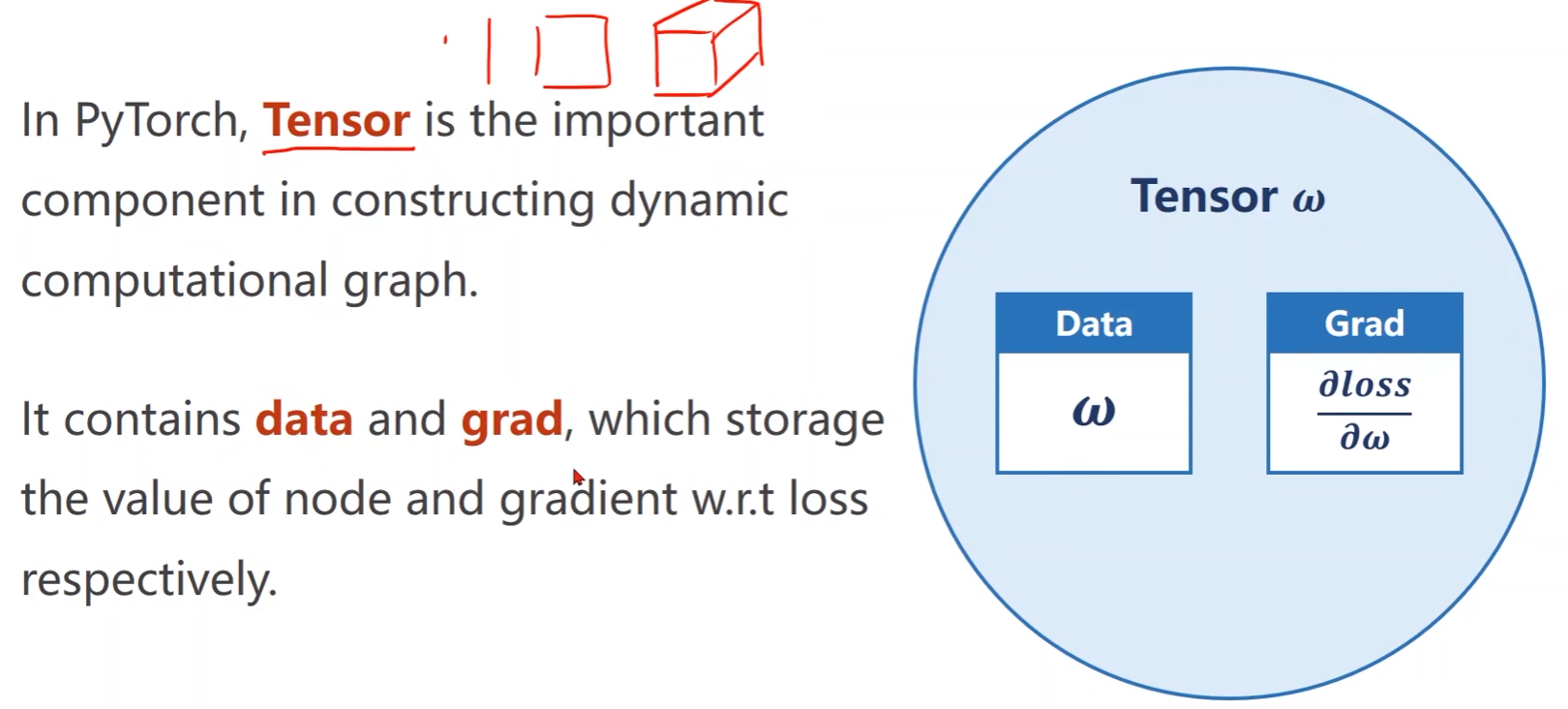
import torch # 导入pytorch库
# 训练集
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
# 权重
w = torch.Tensor([1.0]) # 使用pytorch中的Tensor进行定义赋值
w.requires_grad = True # 表示需要计算梯度,默认的是False,即不计算梯度
def forward(x):
# 定义模型:y_hat = x * w,其中w是一个张量Tensor,因此该乘法*被重载了,变成了Tensor之间的数乘
# x需要为Tensor,如果不是,则会自动转换成Tensor
return x * w
def loss(x, y):
# 定义损失函数loss function
y_pred = forward(x)
return (y_pred - y) ** 2 # (y_hat - y)^2
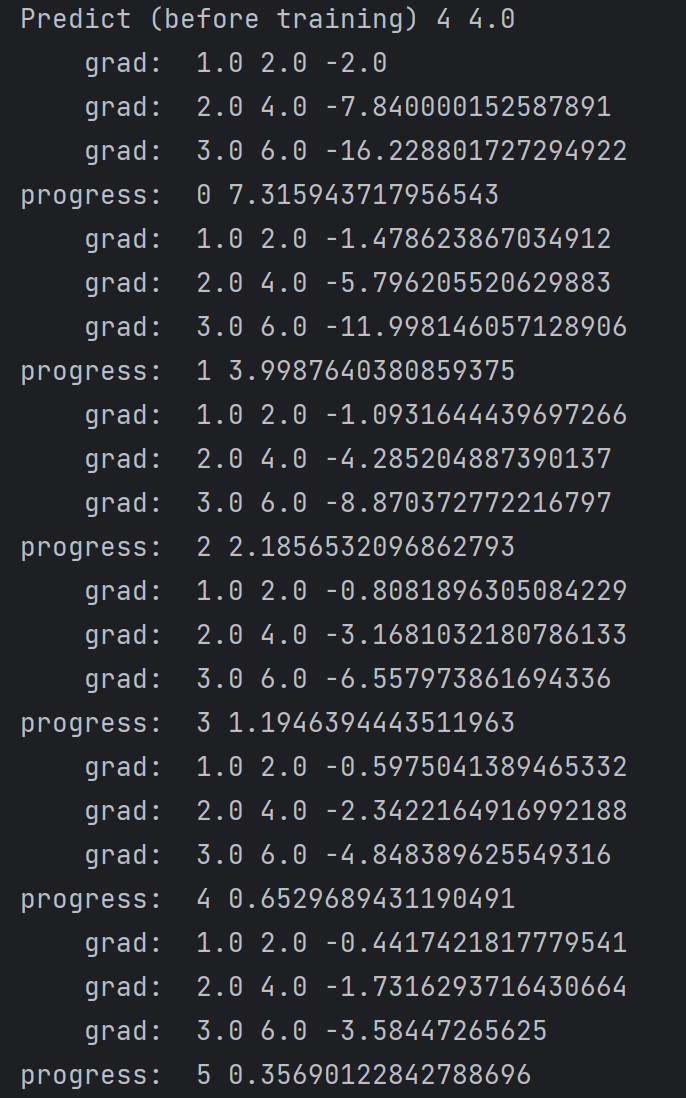
print('Predict (before training)', 4, forward(4).item())
for epoch in range(100):
for x, y in zip(x_data, y_data):
l = loss(x, y) # 计算loss,结果是Tensor(前馈)
l.backward() # 反馈,l是Tensor
print("\tgrad: ", x, y, w.grad.item()) # item是将梯度中的数值取出来作为一个标量
# w是一个张量,包含data和grad,其中grad也是张量,因此是要取grad的数据data
w.data = w.data - 0.01 * w.grad.data
# .data是Tensor操作,.item()是将数值取出来当成标量使用
w.grad.data.zero_() # 更新完成后将梯度清零,否则会被累加到下一轮训练
print("progress: ", epoch, l.item())
print('Predict (after training)', 4, forward(4).item())