- https://www.bilibili.com/video/BV13Q4y197Wg/
动态规划解题步骤 —— carl
动态规划,英文:Dynamic Programming,简称DP,如果某一问题有很多重叠子问题,使用动态规划是最有效的。
所以动态规划中每一个状态一定是由上一个状态推导出来的,这一点就区分于贪心,贪心没有状态推导,而是从局部直接选最优的,
对于动态规划问题,我将拆解为如下五步曲,这五步都搞清楚了,才能说把动态规划真的掌握了!
- 确定dp数组(dp table)以及下标的含义
- 确定递推公式
- dp数组如何初始化
- 确定遍历顺序
- 举例推导dp数组
为什么要先确定递推公式,然后在考虑初始化呢?
因为一些情况是递推公式决定了dp数组要如何初始化!
动态规划应该如何debug
找问题的最好方式就是把dp数组打印出来,看看究竟是不是按照自己思路推导的!
做动规的题目,写代码之前一定要把状态转移在dp数组的上具体情况模拟一遍,心中有数,确定最后推出的是想要的结果。
然后再写代码,如果代码没通过就打印dp数组,看看是不是和自己预先推导的哪里不一样。
发出这样的问题之前,其实可以自己先思考这三个问题:
- 这道题目我举例推导状态转移公式了么?
- 我打印dp数组的日志了么?
- 打印出来了dp数组和我想的一样么?
动态规划套路详解 —— labuladong
动态规划问题(Dynamic Programming)应该是很多读者头疼的,不过这类问题也是最具有技巧性,最有意思的。
首先,动态规划问题的一般形式就是求最值。
动态规划其实是运筹学的一种最优化方法,只不过在计算机问题上应用比较多,比如说让你求最长递增子序列呀,最小编辑距离呀等等。
既然是要求最值,核心问题是什么呢?
求解动态规划的核心问题是穷举。
因为要求最值,肯定要把所有可行的答案穷举出来,然后在其中找最值呗。
动态规划这么简单,就是穷举就完事了?我看到的动态规划问题都很难啊!
首先,动态规划的穷举有点特别,因为这类问题存在「重叠子问题」,如果暴力穷举的话效率会极其低下,所以需要**「备忘录」或者「DP table」来优化穷举过程**,避免不必要的计算。
而且,动态规划问题一定会具备「最优子结构」,才能通过子问题的最值得到原问题的最值。
另外,虽然动态规划的核心思想就是穷举求最值,但是问题可以千变万化,穷举所有可行解其实并不是一件容易的事,只有列出正确的状态转移方程才能正确地穷举。
以上提到的重叠子问题、最优子结构、状态转移方程就是动态规划三要素。
具体什么意思等会会举例详解,但是在实际的算法问题中,写出状态转移方程是最困难的,这也就是为什么很多朋友觉得动态规划问题困难的原因,我来提供我研究出来的一个思维框架,辅助你思考状态转移方程:
明确 base case -> 明确「状态」-> 明确「选择」 -> 定义 dp 数组/函数的含义。
按上面的套路走,最后的结果就可以套这个框架:
明确 base case -> 明确「状态」-> 明确「选择」 -> 定义 dp 数组/函数的含义。
# 初始化 base case
dp[0][0][...] = base
# 进行状态转移
for 状态1 in 状态1的所有取值:
for 状态2 in 状态2的所有取值:
for ...
dp[状态1][状态2][...] = 求最值(选择1,选择2...)
leetcode 509 斐波那契数
- 链接:https://leetcode.cn/problems/fibonacci-number
斐波那契数 (通常用 F(n) 表示)形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是:
F ( 0 ) = 0 , F ( 1 ) = 1 F(0) = 0,F(1) = 1 F(0)=0,F(1)=1
F ( n ) = F ( n − 1 ) + F ( n − 2 ) ,其中 n > 1 F(n) = F(n - 1) + F(n - 2),其中 n > 1 F(n)=F(n−1)+F(n−2),其中n>1
给定 n ,请计算 F ( n ) 。 给定 n ,请计算 F(n) 。 给定n,请计算F(n)。
示例 1:
输入:n = 2
输出:1
解释:F(2) = F(1) + F(0) = 1 + 0 = 1
示例 2:
输入:n = 3
输出:2
解释:F(3) = F(2) + F(1) = 1 + 1 = 2
示例 3:
输入:n = 4
输出:3
解释:F(4) = F(3) + F(2) = 2 + 1 = 3
递归
- 暴力递归
class Solution(object):
def fib(self, n):
"""
:type n: int
:rtype: int
"""
if n<=1:
return n
else:
return self.fib(n-1)+self.fib(n-2)
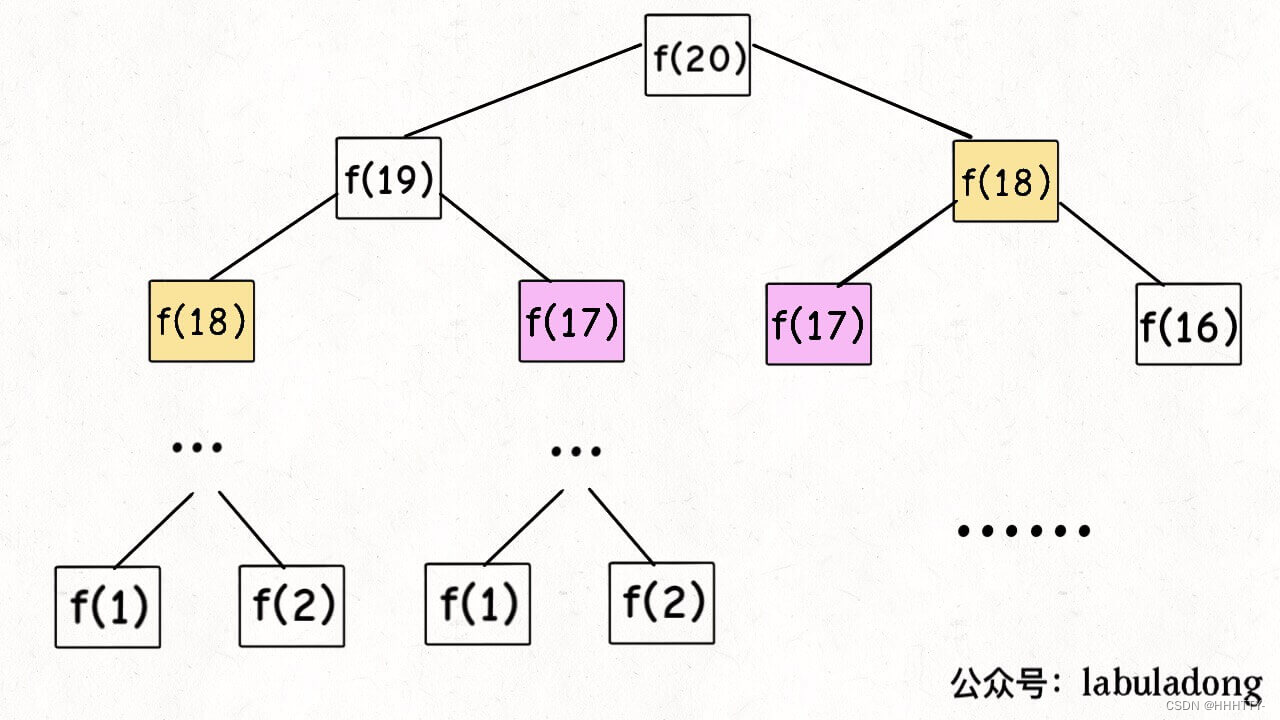
递归过程
递归算法的时间复杂度怎么计算?
就是用子问题个数乘以解决一个子问题需要的时间。
-
首先计算子问题个数,即递归树中节点的总数。显然二叉树节点总数为指数级别,所以子问题个数为 O(2^n)。
-
然后计算解决一个子问题的时间,在本算法中,没有循环,只有 f(n - 1) + f(n - 2) 一个加法操作,时间为 O(1)。
所以,这个算法的时间复杂度为二者相乘,即 O(2^n),指数级别,爆炸。
观察递归树,很明显发现了算法低效的原因:存在大量重复计算,
- 比如 f(18) 被计算了两次,
- 而且你可以看到,以 f(18) 为根的这个递归树体量巨大,多算一遍,会耗费巨大的时间。
- 更何况,还不止 f(18) 这一个节点被重复计算,所以这个算法及其低效。
这就是动态规划问题的第一个性质:重叠子问题。
带备忘录的递归解法
明确了问题,其实就已经把问题解决了一半。
- 即然耗时的原因是重复计算,那么我们可以造一个「备忘录」,每次算出某个子问题的答案后别急着返回,先记到「备忘录」里再返回;
- 每次遇到一个子问题先去「备忘录」里查一查,如果发现之前已经解决过这个问题了,直接把答案拿出来用,不要再耗时去计算了。
一般使用一个数组充当这个「备忘录」,当然你也可以使用哈希表(字典),思想都是一样的。
def help(memo,n):
if n <=1:
return n
if memo[n]!=0:
return memo[n]
memo[n] = help(memo, n-1) + help(memo, n-2)
return memo[n]
class Solution:
def fib(self, n: int) -> int:
if n<=1:
return n
memo = [0] * (n+1)
return help(memo,n)
现在,画出递归树,你就知道「备忘录」到底做了什么。
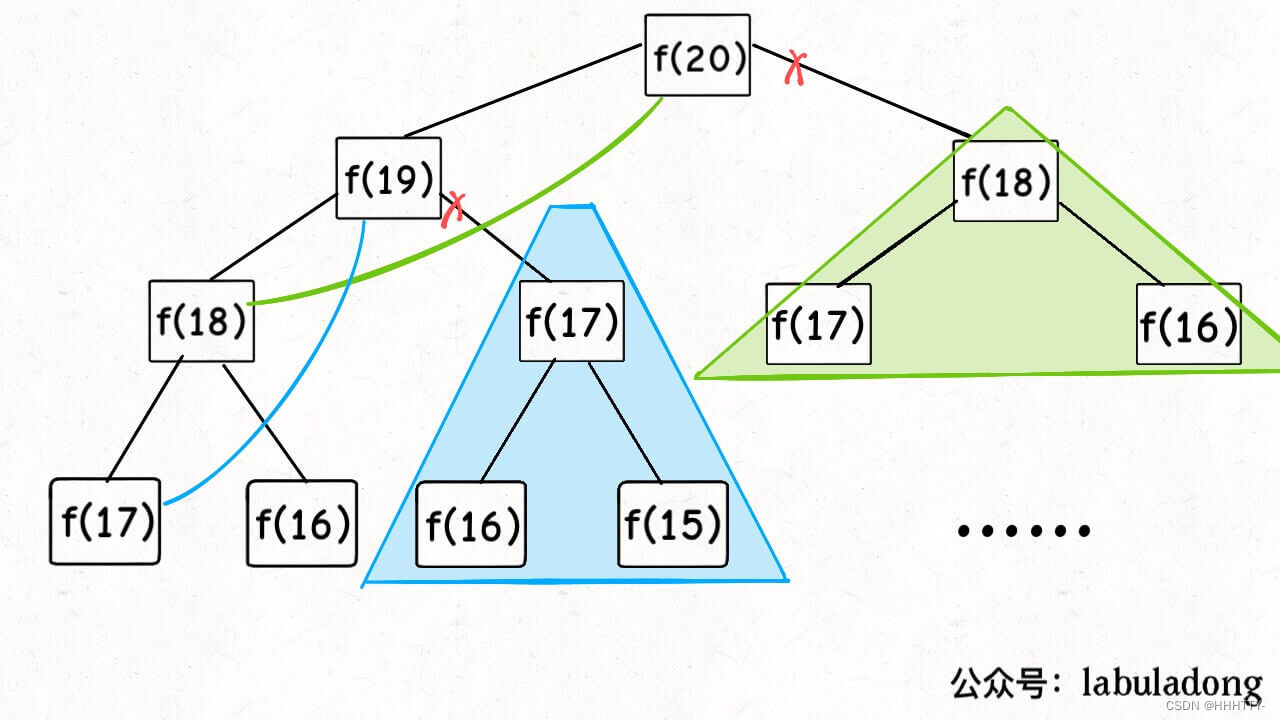
实际上,带「备忘录」的递归算法,把一棵存在巨量冗余的递归树通过「剪枝」,改造成了一幅不存在冗余的递归图,极大减少了子问题(即递归图中节点)的个数。
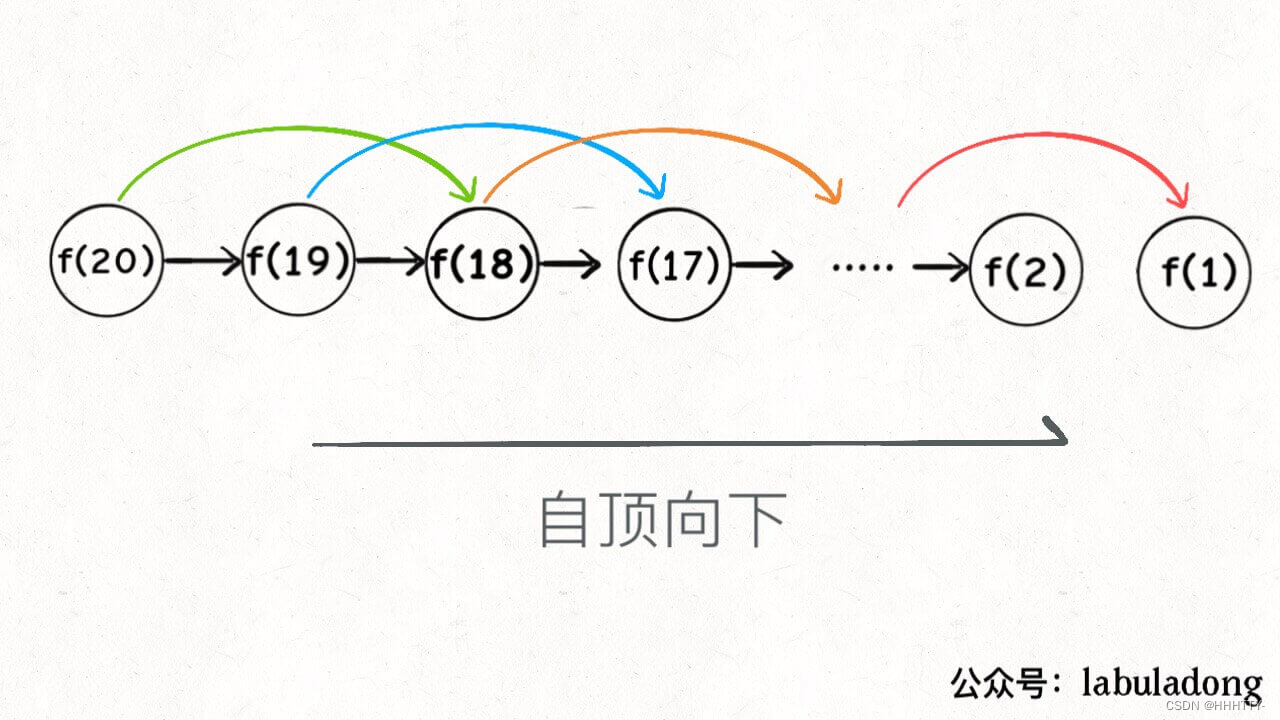
子问题个数,即图中节点的总数,由于本算法不存在冗余计算,子问题就是 f(1), f(2), f(3) … f(20),数量和输入规模 n = 20 成正比,所以子问题个数为 O(n)。
解决一个子问题的时间,同上,没有什么循环,时间为 O(1)。
所以,本算法的时间复杂度是 O(n)。比起暴力算法,是降维打击。
至此,带备忘录的递归解法的效率已经和迭代的动态规划解法一样了。
实际上,这种解法和迭代的动态规划已经差不多了,只不过这种方法叫做「自顶向下」,动态规划叫做「自底向上」。
啥叫「自顶向下」?注意我们刚才画的递归树(或者说图),是从上向下延伸,都是从一个规模较大的原问题比如说 f(20),向下逐渐分解规模,直到 f(1) 和 f(2) 这两个 base case,然后逐层返回答案,这就叫「自顶向下」。
啥叫「自底向上」?反过来,我们直接从最底下,最简单,问题规模最小的 f(1) 和 f(2) 开始往上推,直到推到我们想要的答案 f(20),这就是动态规划的思路,这也是为什么动态规划一般都脱离了递归,而是由循环迭代完成计算。
动态规划 (dp 数组的迭代解法)
动规五部曲:
这里我们要用一个一维dp数组来保存递归的结果
-
确定dp数组以及下标的含义
dp[i]的定义为:第i个数的斐波那契数值是dp[i] -
确定递推公式
为什么这是一道非常简单的入门题目呢?
因为题目已经把递推公式直接给我们了:状态转移方程 dp[i] = dp[i - 1] + dp[i - 2] -
dp数组如何初始化
题目中把如何初始化也直接给我们了,如下:
dp[0] = 0;
dp[1] = 1;
-
确定遍历顺序
从递归公式dp[i] = dp[i - 1] + dp[i - 2];中可以看出,dp[i]是依赖 dp[i - 1] 和 dp[i - 2],那么遍历的顺序一定是从前到后遍历的 -
举例推导dp数组
按照这个递推公式 d p [ i ] = d p [ i − 1 ] + d p [ i − 2 ] dp[i] = dp[i - 1] + dp[i - 2] dp[i]=dp[i−1]+dp[i−2],我们来推导一下,当N为10的时候,dp数组应该是如下的数列:
0 1 1 2 3 5 8 13 21 34 55
如果代码写出来,发现结果不对,就把dp数组打印出来看看和我们推导的数列是不是一致的。
class Solution:
def fib(self, n: int) -> int:
# 创建 dp table
dp = [1] * (n+1)
# 排除 Corner Case
if n<=1:
return n
# 初始化 dp 数组
dp[0]=0
dp[1]=1
# 遍历顺序: 由前向后。因为后面要用到前面的状态
for i in range(2,n+1):
# 确定递归公式/状态转移公式
dp[i]=dp[i-1]+dp[i-2]
# 返回答案
return dp[-1]
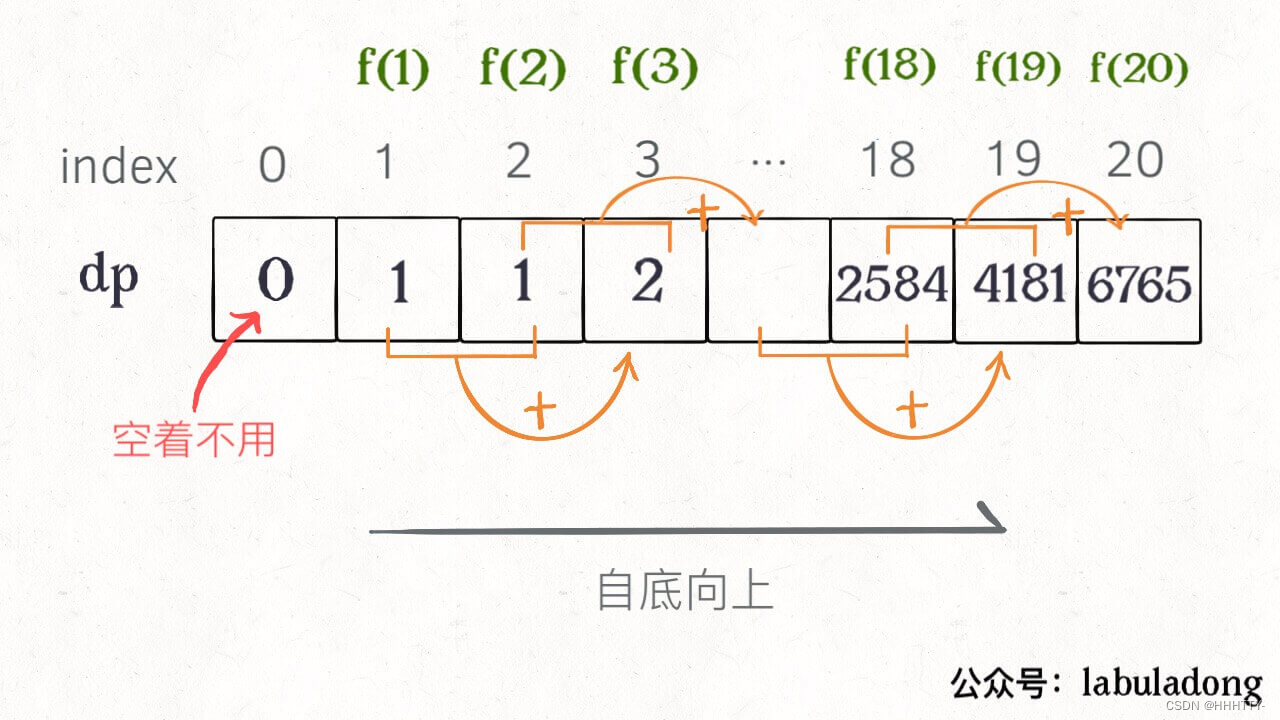
画个图就很好理解了,而且你发现这个 DP table 特别像之前那个「剪枝」后的结果,只是反过来算而已。
- 实际上,带备忘录的递归解法中的「备忘录」,最终完成后就是这个 DP table,所以说这两种解法其实是差不多的,大部分情况下,效率也基本相同。
这里,引出「状态转移方程」这个名词,实际上就是描述问题结构的数学形式:
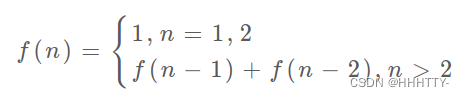
为啥叫「状态转移方程」?
其实就是为了听起来高端。你把 f(n) 想做一个状态 n,这个状态 n 是由状态 n - 1 和状态 n - 2 相加转移而来,这就叫状态转移,仅此而已。
你会发现,上面的几种解法中的所有操作,例如 r e t u r n f ( n − 1 ) + f ( n − 2 ) , d p [ i ] = d p [ i − 1 ] + d p [ i − 2 ] return f(n - 1) + f(n - 2),dp[i] = dp[i - 1] + dp[i - 2] returnf(n−1)+f(n−2),dp[i]=dp[i−1]+dp[i−2],以及对备忘录或 DP table 的初始化操作,都是围绕这个方程式的不同表现形式。
- 可见列出「状态转移方程」的重要性,它是解决问题的核心。
- 而且很容易发现,其实状态转移方程直接代表着暴力解法。
千万不要看不起暴力解,动态规划问题最困难的就是写出这个暴力解,即状态转移方程。
- 只要写出暴力解,优化方法无非是用备忘录或者 DP table,再无奥妙可言。
有人会问,动态规划的另一个重要特性「最优子结构」,怎么没有涉及?
下面会涉及。斐波那契数列的例子严格来说不算动态规划,因为没有涉及求最值,以上旨在说明重叠子问题的消除方法,演示得到最优解法逐步求精的过程。
下面,看第二个例子,凑零钱问题。