本文转载自根据相关性生成变量
已知一组变量a,想要生成另一组变量b,要求a与b之间相关性为c。
实现思路如下:
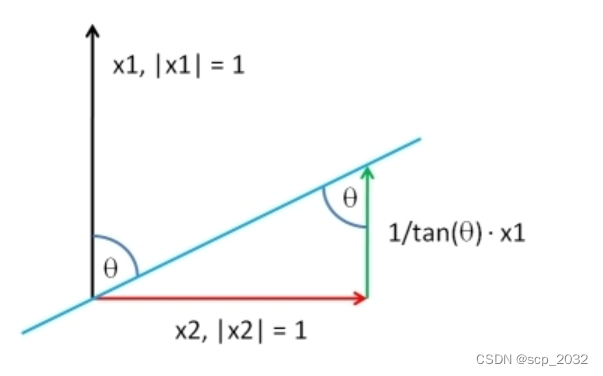
- 设固定变量为x1,随机变量x2,相关系数为rho。x1与x2之间的相关性可以转化为向量之间的夹角问题,问题就转变为了求与已知向量夹角为θ的变量。
- 首先将变量x1与x2中心化,然后将x2转化为x1的正交向量,并将两者均缩放到1.
- 目的向量即为x2 +(1/tan(θ))* x1.
- 如图所示
实现代码如下
n <- 20 # length of vector
rho <- 0.6 # desired correlation = cos(angle)
theta <- acos(rho) # corresponding angle
x1 <- rnorm(n, 1, 1) # fixed given data
x2 <- rnorm(n, 2, 0.5) # new random data
X <- cbind(x1, x2) # matrix
Xctr <- scale(X, center=TRUE, scale=FALSE) # centered columns (mean 0)
Id <- diag(n) # identity matrix
Q <- qr.Q(qr(Xctr[ , 1, drop=FALSE])) # QR-decomposition, just matrix Q
P <- tcrossprod(Q) # = Q Q' # projection onto space defined by x1
x2o <- (Id-P) %*% Xctr[ , 2] # x2ctr made orthogonal to x1ctr
Xc2 <- cbind(Xctr[ , 1], x2o) # bind to matrix
Y <- Xc2 %*% diag(1/sqrt(colSums(Xc2^2))) # scale columns to length 1
x <- Y[ , 2] + (1 / tan(theta)) * Y[ , 1] # final new vector
cor(x1, x) # check correlation = rho
如果是想要实现生成相关性矩阵,可以使用循环。
correlation <- function(y,rho,x){
#y,x均为相同维度的矩阵,rho与x,y的列数相同,实现列之间的相关性数据生成
for (i in 1:length(rho)){
y_1 <- y[, i]
rho_1 <- rho[i]
x_1 <- x[, i]
n <- length(y_1) #读取数据
theta <- acos(rho_1) #将相关性转化为角度
xctr <- scale(cbind(x_1,y_1),center = TRUE, scale = FALSE) #将x、y中心化
id <- diag(n) #生成对角矩阵
q <- qr.Q(qr(xctr[ , 1, drop = FALSE])) #qr分解
p <- tcrossprod(q) #定义投影
x2o <- (id-p) %*% xctr[ ,2]
xc2 <- cbind(xctr[ ,1], x2o)
Y <- xc2 %*% diag(1/sqrt(colSums(xc2^2)))
y[, i] <- Y[ ,2] + (1/tan(theta))* Y[, 1] #输出y
}
return(y)
}