1.概述
提到B+树就不得不提及二叉树,平衡二叉树和B树这三种数据结构了。B+树就是从他们三个演化来的。众所周知B+树是一种常见的数据结构,被广泛应用于数据库和文件系统等领域,B+树的设计目标是保持树的平衡性,以提供稳定的性能,并且适用于大规模数据存储。B+树由一个根节点、内部节点和叶子节点组成,其中内部节点用于索引和导航,而叶子节点存储实际的数据。
2.B+树基本结构
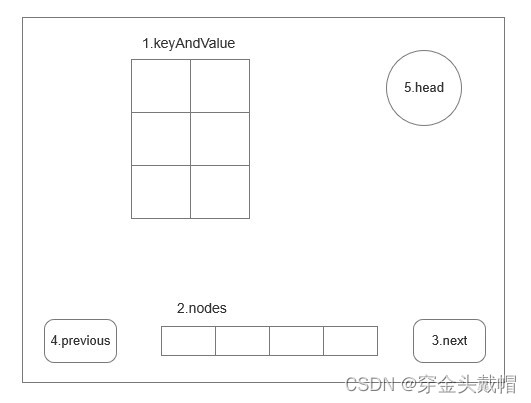
1.keyAndValue:键值对--key是标识;value是存储的具体数据
2.node:节点的子节点,存储的是具体的子节点
3.next:节点的后节点,标记后一个节点
4.previous:节点的前节点,标记前一个节点
5.head:节点的父节点,标记本机的父节点
3.探索三层结构
此部分依据以下图片展开描述

B+树的结构图
上图的结果是按照B+树的原理添加13个数据以java代码实现的结果,通过过图片的形式可视化了
此次实现我们将阶数设定为了4阶
4.深入了解节点的生成
以上图片的结果是怎么实现的呢,下面我们将展开描述
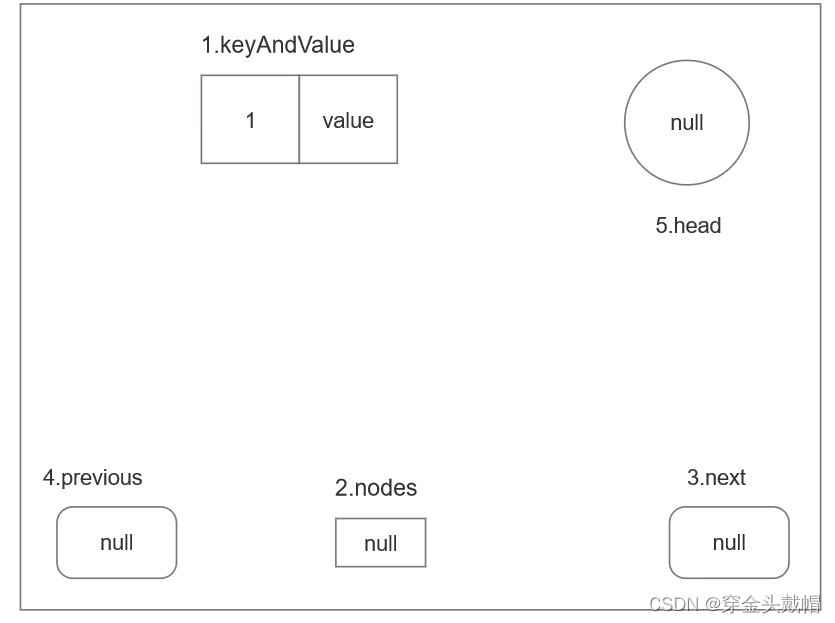
4.1 存储第一条数据
存储第一条数据时此时没有节点,首先判断有没有头节点,没有头节点就将第一条数据添加到一个存放键值对的集合keyAndValue中,并依据此集合初始化一个节点,并将这个新初始化节点分别标记为根节点和头节点。此结果如下图
4.2 单个节点
没有超过设定的阶数
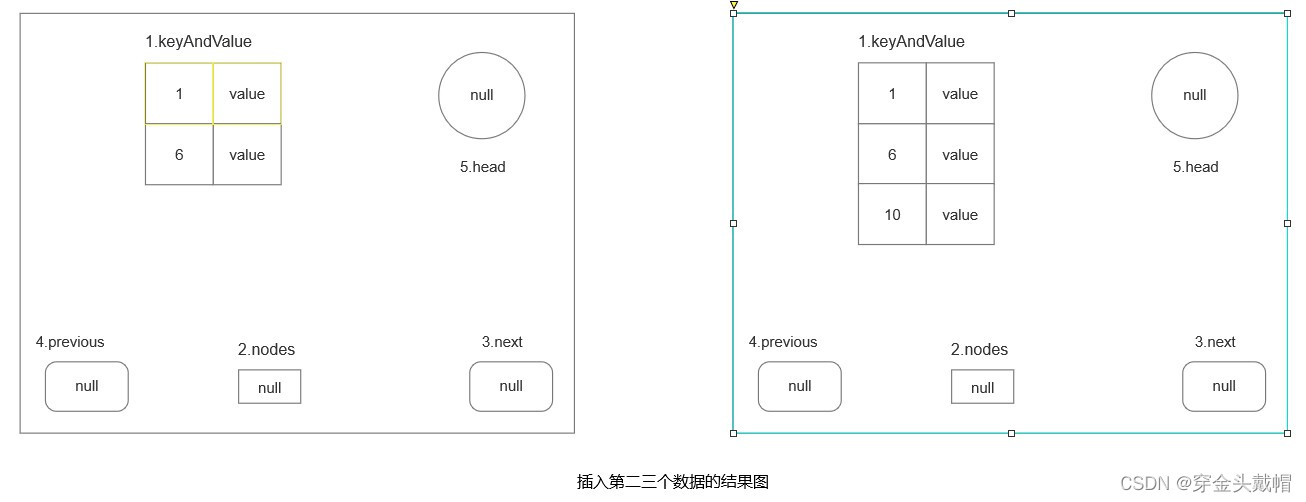
当存储第二和三个数据时,首先判断是否是最后一个结点或者要插入的键值对的键的值是否小于下一个结点的的键的最小值。如果是则再判断有没有超过设定的阶数,没有则将将数据直接插入到当前结点。当前的结点是最后一个结点并且没有超过设定的阶数,因此直接将二三个数据直接插入到当前的结点当中 。 效果入下图所示
超过设定的阶数
在存储第四个数时,首先判断是否是最后一个结点或者要插入的键值对的键的值是否小于下一个结点的的键的最小值。如果是再判断是否超过设定的阶数了,超过了则取出原来key-value 集合中间位置的下标mid并获得中间位置的键midKey。构造一个新的键值对midKeyAndValue存储(中间位置的键,空串),然后分别将中间位置的左边封装成集合对象leftKeyAndValue,并将左边的数存储到leftKeyAndValue中;中间位置的右边封装成集合对象rightKeyAndValue,再判断当前节点是否有叶子结点,如果有则将中间位置后的数据(不包含中间位置的数据)存储到rightKeyAndValue中;如果没有则将从中间位置开始右边的数据保存到rightKeyAndValue中。分别对左右两个集合对象进行排序处理。以mid为界限将当前结点分裂成两个结点分别是:前节点leftNode,后节点rightNode;前指针的节点的结构为:数据(leftKeyAndValue),子节点(null),前指针(当前节点的左节点),后指针(rightNode),父节点(当前结点的父节点);此时将头节点重置为前节点leftNode;新建一个子节点childNode并将前节点leftNode和后节点rightNode添加进去,然后构造一个父节点parentNode结构为:子节点(childNode),键值对(midKeyAndValue),前节点(null),后节点(null),父节点(null)。并将子节点与父节点进行关联。将当前父节点设置为根节点。此时就转变成“一父二子”了;结果如下图

4.3三个节点
在上图节点的基础上我们再添加第六个数据时(如下图)节点超过阶数就会分裂,以下是分裂时的情况
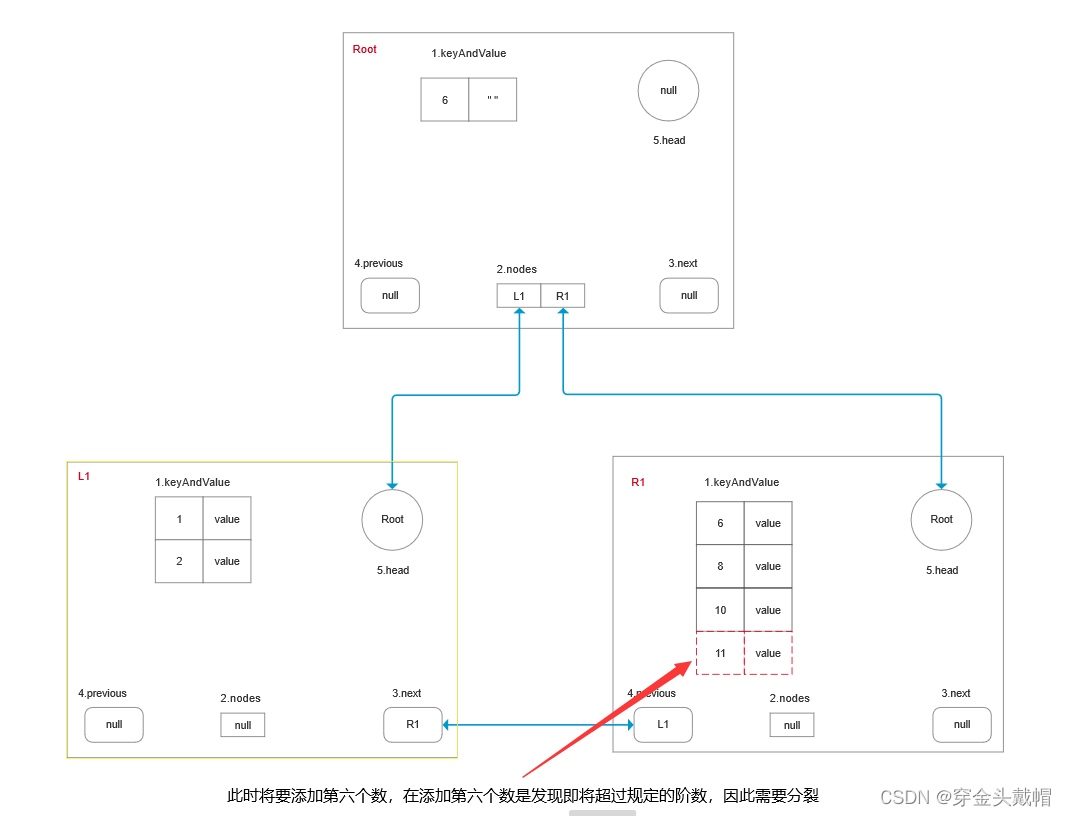
超过阶数
在添加第六条数据的时候首先以L1节点为head判断是否是最后一个结点或者要插入的键值对的键的值是否小于下一个结点的的键的最小值。
1.如果是再判断是否超过设定的阶数了,此时设定的场景是要超过设定的阶数,先取出L1节点的key-value 集合中间位置的下标mid并获得中间位置的键midKey。构造一个新的键值对midKeyAndValue存储(中间位置的键,空串),然后分别将中间位置的左边封装成集合对象leftKeyAndValue,并将左边的数存储到leftKeyAndValue中;中间位置的右边封装成集合对象rightKeyAndValue,再判断当前节点是否有叶子结点,如果有则将中间位置后的数据(不包含中间位置的数据)存储到rightKeyAndValue中;如果没有则将从中间位置开始右边的数据保存到rightKeyAndValue中。分别对左右两个集合对象进行排序处理。以mid为界限将当前结点分裂成两个结点分别是:前节点leftNode,后节点rightNode;前指针的节点的结构为:数据(leftKeyAndValue),子节点(null),前指针(当前节点的左节点),后指针(rightNode),父节点(当前结点的父节点),新建一个子节点集合childNodes并分别将前节点leftNode,后节点rightNode添加进去;如果头结点是当前要分隔的节点则将头节点重置为前节点leftNode,获取到当前L1节点的父节点parentNode,并获取到父节点的所有子节点,将这些子节点全部添加到子节点集合childNodes中,然后删除当前的L1节点,然后将子节点重置成新的子节点集合childNodes;继续以父节点为依据判断是否超过设定的阶数了,此时没有超过阶数,将键值对midKeyAndValue直接保存到当前的父节点中,并进行排序操作,此时就变成“一夫三子”了
2.如果不是最后一个结点或者要插入的键值对的键的值大于下一个结点的的键的最小值,此时移动指针,将R1作为依据再进行判断是否是最后一个结点或者要插入的键值对的键的值是否小于下一个结点的的键的最小值,此时肯定符合条件的,再判断是否超过设定的阶数了,此时设定的场景是要超过设定的阶数,先取出R1节点的key-value 集合中间位置的下标mid并获得中间位置的键midKey。构造一个新的键值对midKeyAndValue存储(中间位置的键,空串),然后分别将中间位置的左边封装成集合对象leftKeyAndValue,并将左边的数存储到leftKeyAndValue中;中间位置的右边封装成集合对象rightKeyAndValue,再判断当前节点是否有叶子结点,如果有则将中间位置后的数据(不包含中间位置的数据)存储到rightKeyAndValue中;如果没有则将从中间位置开始右边的数据保存到rightKeyAndValue中。分别对左右两个集合对象进行排序处理。以mid为界限将当前结点分裂成两个结点分别是:前节点leftNode,后节点rightNode;前指针的节点的结构为:数据(leftKeyAndValue),子节点(null),前指针(当前节点的左节点),后指针(rightNode),父节点(当前结点的父节点),新建一个子节点集合childNodes并分别将前节点leftNode,后节点rightNode添加进去;如果头结点是当前要分隔的节点则将头节点重置为前节点leftNode,获取到当前L1节点的父节点parentNode,并获取到父节点的所有子节点,将这些子节点全部添加到子节点集合childNodes中,然后删除当前的R1节点,然后将子节点重置成新的子节点集合childNodes;继续以父节点为依据判断是否超过设定的阶数了,此时没有超过阶数,将键值对midKeyAndValue直接保存到当前的父节点中,并进行排序操作,生成一个一父三子的结构如下图()
4.4八个节点
一父四子后再添加数据,部分满跟都满都会使得节点再次分裂,分裂成一父二子的情况
在添加数据的时候首先以左边第一个节点为head判断是否是最后一个结点或者要插入的键值对的键的值是否小于下一个结点的的键的最小值。
1.如果是再判断是否超过设定的阶数了,此时设定的场景是要超过设定的阶数,先取出当前节点的key-value 集合中间位置的下标mid并获得中间位置的键midKey。构造一个新的键值对midKeyAndValue存储(中间位置的键,空串),然后分别将中间位置的左边封装成集合对象leftKeyAndValue,并将左边的数存储到leftKeyAndValue中;中间位置的右边封装成集合对象rightKeyAndValue,再判断当前节点是否有叶子结点,如果有则将中间位置后的数据(不包含中间位置的数据)存储到rightKeyAndValue中;如果没有则将从中间位置开始右边的数据保存到rightKeyAndValue中。分别对左右两个集合对象进行排序处理。以mid为界限将当前结点分裂成两个结点分别是:前节点leftNode,后节点rightNode;前指针的节点的结构为:数据(leftKeyAndValue),子节点(null),前指针(当前节点的左节点),后指针(rightNode),父节点(当前结点的父节点),新建一个子节点集合childNodes并分别将前节点leftNode,后节点rightNode添加进去;如果头结点是当前要分隔的节点则将头节点重置为前节点leftNode,获取到当前节点的父节点parentNode,并获取到父节点的所有子节点,将这些子节点全部添加到子节点集合childNodes中,然后删除当前节点,然后将子节点重置成新的子节点集合childNodes;
2.继续以父节点为依据判断是否超过设定的阶数了,此时超过阶数,超过了则取出原来key-value 集合中间位置的下标mid并获得中间位置的键midKey。构造一个新的键值对midKeyAndValue存储(中间位置的键,空串),然后分别将中间位置的左边封装成集合对象leftKeyAndValue,并将左边的数存储到leftKeyAndValue中;中间位置的右边封装成集合对象rightKeyAndValue,再判断当前节点是否有叶子结点,如果有则将中间位置后的数据(不包含中间位置的数据)存储到rightKeyAndValue中;如果没有则将从中间位置开始右边的数据保存到rightKeyAndValue中。分别对左右两个集合对象进行排序处理。以mid为界限将当前结点分裂成两个结点分别是:前节点leftNode,后节点rightNode;前指针的节点的结构为:数据(leftKeyAndValue),子节点(null),前指针(当前节点的左节点),后指针(rightNode),父节点(当前结点的父节点);判断当前结点是否有孩子节点,此场景是有孩子节点的,获取到所有孩子节点存储在nodes集合中,并新建两个集合leftNodes与rightNodes分别存储左节点的子节点与右节点的子节点,通过遍历取得当前孩子节点的最大键值,小于mid的键的数是左节点的子节点;大于mid的键的数是右节点的子节点,将leftNodes添加为leftNode的子节点;将rightNodes添加为rightNode的子节点。此时将头节点重置为前节点leftNode;新建一个子节点childNode并将前节点leftNode和后节点rightNode添加进去;然后判断当前结点是否有父节点,此时有父节点,获取到当前节点的父节点parentNode,并获取到父节点的所有子节点,将这些子节点全部添加到子节点集合childNodes中,然后删除当前的节点,然后将子节点重置成新的子节点集合childNodes;继续以父节点为依据判断是否超过设定的阶数了,此时没有超过阶数,将键值对midKeyAndValue直接保存到当前的父节点中,并进行排序操作。最终效果如下图所示()
4.5 java代码实现
1.创建一个B+树的容器对象Node.java-描述节点的基本结构
package com.sbxBase.testBTree;
import java.util.List;
/*节点类*/
public class Node {
//children
//节点的子节点
private List<Node> nodes;
//节点的键值对
private List<KeyAndValue> keyAndValue;
//节点的后节点
private Node nextNode;
//节点的前节点
private Node previousNode;
//节点的父节点
private Node parantNode;
public Node( List<Node> nodes, List<KeyAndValue> keyAndValue, Node nextNode,Node previousNode, Node parantNode) {
this.nodes = nodes;
this.keyAndValue = keyAndValue;
this.nextNode = nextNode;
this.parantNode = parantNode;
this.previousNode = previousNode;
}
boolean isLeaf() {
return nodes==null;
}
boolean isHead() {
return previousNode == null;
}
boolean isTail() {
return nextNode == null;
}
boolean isRoot() {
return parantNode == null;
}
List<Node> getNodes() {
return nodes;
}
void setNodes(List<Node> nodes) {
this.nodes = nodes;
}
List<KeyAndValue> getKeyAndValue() {
return keyAndValue;
}
Node getNextNode() {
return nextNode;
}
void setNextNode(Node nextNode) {
this.nextNode = nextNode;
}
Node getParantNode() {
return parantNode;
}
void setParantNode(Node parantNode) {
this.parantNode = parantNode;
}
Node getPreviousNode() {
return previousNode;
}
void setPreviousNode(Node previousNode) {
this.previousNode = previousNode;
}
}2.创建一个数据存储对象KeyAndValue.java存储要保存到节点中的数据
package com.sbxBase.testBTree;
import java.util.ArrayList;
import java.util.Collections;
public class KeyAndValue implements Comparable<KeyAndValue>{
/*存储索引关键字*/
private int key;
/*存储数据*/
private Object value;
@Override
public int compareTo(KeyAndValue o) {
//根据key的值升序排列 从小到大
// 1 3 4 6
// 0 1 2 3
return this.key - o.key;
}
public int getKey() {
return key;
}
public void setKey(int key) {
this.key = key;
}
public Object getValue() {
return value;
}
public void setValue(Object value) {
this.value = value;
}
KeyAndValue(int key, Object value) {
this.key = key;
this.value = value;
}
}3.B+树逻辑实现代码--处理
package com.sbxBase.testBTree;
import org.springframework.util.StringUtils;
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
public class MyBtree {
//B+树的阶数
private int rank;
//根节点
private Node root;
//头结点
private Node head;
MyBtree(int rank) {
this.rank = rank;
}
public Node getRoot() {
return root;
}
public void insert(KeyAndValue entry) {
//新建一个容器存储键值对
List<KeyAndValue> keyAndValueArrayList = new ArrayList<KeyAndValue>();
//插入第一个数据的时候
if (head == null) {
keyAndValueArrayList.add(entry);
root = new Node(null, keyAndValueArrayList, null, null, null);
head = new Node(null, keyAndValueArrayList, null, null, null);
} else {
Node node = head;
while (node != null) {
List<KeyAndValue> keyAndValue = node.getKeyAndValue();
for (KeyAndValue KV : keyAndValue) {
if (KV.getKey() == entry.getKey()) {
KV.setValue(entry.getValue());
return;
}
}
//如果当前结点为最后结点或者当前数据的键大于当前节点的下一个节点的键值对中最小的键值
if (node.getNextNode() == null || entry.getKey() <= node.getNextNode().getKeyAndValue().get(0).getKey()) {
splidNode(node, entry);
break;
}
//移动指针
node = node.getNextNode();
}
}
}
/**
* [方法概述]:
* 处理节点、节点的键值对。
* [业务逻辑]:
* 首先判断当前节点的键值对是否超过阶数。
* 1.如果没超过则将新的键值对插入到当前节点的键值对中。
* 2.如果超过:
* 2.1 则将节点,和节点的键值对进行拆分。
* 首先先将当前节点的键值对÷2获得中间下标,根据中间下标拆分为左右两部分。 (左键值对是当前数字较小的,右键值对是数字较大的)
* 再将节点进行拆分。生成左右两个节点。左节点的nextNode属性指向右节点,左节点的previousNode属性指向当前节点前节点的nextNode。右节点的previousNode属性指向左节点,右节点的nextNode属性指向当前节点后节点的previousNode。形成双向链表结构。并将上一步的左右键值对分别保存到左右节点中。
* 2.2 判断是否有子节点
* 如果有子节点,就将当前节点的所有子节点的最大键值与中间下标的键进行比较,小于中间下标键的子节点保存到左节点的子节点中,大于中间下标键的子节点保存到右节点的子节点中
* 2.3 判断是否有前后节点
* 如果当前节点有前后节点,将2.1中的左节点保存到前节点的nextNode属性中,将右节点保存到后节点的previousNode属性中
* 2.4 判断当前节点是否有父节点:
* 如果有父节点则将父节点保存到左右节点中。在将左右节点存放到父节点的nodes属性中。也形成了类似链表的结构。使得父子节点之间建立联系。并移除当前节点,在对当前节点的父节点进行递归,检查父节点是否超出阶数
* 如果没有父节点。则生成一个父节点,将中间下标的值存放到父节点的键值对中()。在将左右节点存放到父节点的nodes属性中。然后将父节点保存在左右节点的parantNode属性。
* <p>
* ? 将中间下标的值存放到父节点的键值对中:
* 因为将当前节点拆分成两部分后需要指向一个父节点,根据父节点去区分左右两部分,当前节点的中间下标值可以起到这个作用所以才将中间下标的值存放到父节点的键值对中
* ?为什么移除当前节点:
* 因为已经将当前节点拆分成两个新节点了,因此不需要当前节点了
*
* @param node 当前节点
* @param entry 键值对
*/
private void splidNode(Node node, KeyAndValue entry) {
List<KeyAndValue> keyAndValues = node.getKeyAndValue();
//将数据添加到节点的键值对中,并排序
keyAndValues.add(entry);
Collections.sort(keyAndValues);
//判断当前节点的键值是否超过规定阶数
if (keyAndValues.size() == rank) {
//取出当前节点键值对的中间位置及数据数据
int mid = keyAndValues.size() / 2;
int key = keyAndValues.get(mid).getKey();
//存储作为某个节点的根节点的键值对
KeyAndValue midKeyAndValue = new KeyAndValue(key, "");
//存储左节点的键值对
List<KeyAndValue> leftKeyAndValue = new ArrayList<>();
for (int i = 0; i < mid; i++) {
leftKeyAndValue.add(keyAndValues.get(i));
}
//存储右节点的键值对
List<KeyAndValue> rightKeyAndValue = new ArrayList<>();
int k = node.isLeaf() ? mid : mid + 1;
for (int i = k; i < rank; i++) {
rightKeyAndValue.add(keyAndValues.get(i));
}
//排序
Collections.sort(leftKeyAndValue);
Collections.sort(rightKeyAndValue);
//创建左右节点
Node rightNode;
Node leftNode;
leftNode = new Node(null, leftKeyAndValue, null, node.getPreviousNode(), node.getParantNode());
rightNode = new Node(null, rightKeyAndValue, node.getNextNode(), leftNode, node.getParantNode());
leftNode.setNextNode(rightNode);
//判断当前节点是否有子节点
if (node.getNodes() != null) {
List<Node> nodes = node.getNodes();
List<Node> leftnodes = new ArrayList<>();
List<Node> rightnodes = new ArrayList<>();
for (Node node1 : nodes) {
int max = node1.getKeyAndValue().get(node1.getKeyAndValue().size() - 1).getKey();
if (midKeyAndValue.getKey() > max) {
leftnodes.add(node1);
node1.setParantNode(leftNode);
} else {
rightnodes.add(node1);
node1.setParantNode(rightNode);
}
}
leftNode.setNodes(leftnodes);
rightNode.setNodes(rightnodes);
}
//当前节点如果有前节点,将左节点添加为前节点的后节点
if (node.getPreviousNode() != null) {
node.getPreviousNode().setNextNode(leftNode);
}
//当前节点有后节点,将右节点添加为后节点的前节点
if (node.getNextNode() != null) {
node.getNextNode().setPreviousNode(rightNode);
}
//如果当前拆分的节点是头节点,则将左节点作为头节点
if (node == head) {
head = leftNode;
}
List<Node> childNodes = new ArrayList<>();
childNodes.add(leftNode);
childNodes.add(rightNode);
if (node.getParantNode() == null) {
List<KeyAndValue> partentKeyAndValues = new ArrayList<>();
partentKeyAndValues.add(midKeyAndValue);
//创建父节点
Node partentNode = new Node(childNodes, partentKeyAndValues, null, null, null);
leftNode.setParantNode(partentNode);
rightNode.setParantNode(partentNode);
root = partentNode;
} else {
Node parantNode = node.getParantNode();
//将所有的子节点整合在一起
childNodes.addAll(parantNode.getNodes());
//移除当前节点
childNodes.remove(node);
//将新的子节点放入父节点的子节点中
parantNode.setNodes(childNodes);
//左右节点都添加父节点
leftNode.setParantNode(parantNode);
rightNode.setParantNode(parantNode);
//父节点的父节点为空,此父节点为根节点
if (parantNode.getParantNode() == null) {
root = parantNode;
}
//当前节点有父节点,继续调用此方法,对父节点进行判断拆分
splidNode(parantNode, midKeyAndValue);
}
}
}
/**
* [方法概述]:
* 打印B+树 传来的节点和这个节点的子子孙孙
* [业务逻辑]:
* 1.判断次节点是否是根节点:
* 如果是就将打印根节点内的元素
* 2.判断此节点是否为空:
* 如果为空就返回
* 3.判断此节点的子节点是否为空:
* 如果不为空,拿到当前节点的子节点并循环遍历,
* 3.1判断子节点是否有前节点:
* 如果没有,将此节点约定为最左节点,并保存当前节点
* 3.2while循环读打印左子节点内的元素,打印完成之后将左子节点的右节点重置为左节点,再进行遍历
* 3.3然后再对此节点的最左节点进行递归查询
*
* @param root 根节点
*/
void printBtree(Node root) {
if (root == this.root) {
//打印根节点内的元素
printNode(root);
System.out.println();
}
if (root == null) {
return;
}
//打印子节点的元素
if (root.getNodes() != null) {
//找到最左边的节点
Node leftNode = null;
Node tmpNode = null;
List<Node> childNodes = root.getNodes();
for (Node node : childNodes) {
if (node.getPreviousNode() == null) {
leftNode = node;
tmpNode = node;
}
}
while (leftNode != null) {
//从最左边的节点向右打印
printNode(leftNode);
System.out.print("|");
leftNode = leftNode.getNextNode();
}
System.out.println();
printBtree(tmpNode);
}
}
/**
* 打印节点内的元素
* 1.获取到当前节点的键值对集合,循环遍历的打印
*
* @param node
*/
private void printNode(Node node) {
List<KeyAndValue> keyAndValues = node.getKeyAndValue();
String key = "";
for (KeyAndValue keyAndValue : keyAndValues) {
key = StringUtils.isEmpty(key)? ""+keyAndValue.getKey():","+keyAndValue.getKey();
}
System.out.print(key);
}
}
4.定义一个方法入口
package com.sbxBase.testBTree;
public class TestMain {
public static void main(String[] args) {
MyBtree btree = new MyBtree(4);//4是生成B+树的阶数
btree.insert( new KeyAndValue(1, "123"));
btree.insert(new KeyAndValue(6, "123"));
btree.insert(new KeyAndValue(10, "123"));
btree.insert(new KeyAndValue(2, "123"));
btree.insert(new KeyAndValue(8, "546"));
btree.insert(new KeyAndValue(11, "123"));
btree.insert(new KeyAndValue(18, "12345"));
btree.insert(new KeyAndValue(3, "123"));
btree.insert(new KeyAndValue(15, "12345"));
btree.insert(new KeyAndValue(17, "12345"));
btree.insert(new KeyAndValue(12, "123"));
btree.insert(new KeyAndValue(13, "123"));
btree.insert(new KeyAndValue(4, "123"));
btree.insert(new KeyAndValue(9, "123"));
btree.insert(new KeyAndValue(19, "12345"));
btree.insert(new KeyAndValue(16, "12345"));
btree.insert(new KeyAndValue(5, "123"));
btree.insert(new KeyAndValue(20, "12345"));
btree.insert(new KeyAndValue(7, "12300"));
btree.insert(new KeyAndValue(21, "12345"));
btree.printBtree(btree.getRoot());
}
}