一、拓扑排序

1.1 什么是拓扑排序

对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序，是将G中所有顶点排成一个线性序列，使得图中任意一对顶点u和v，若边<u,v>∈E(G)，则u在线性序列中出现在v之前。通常，这样的线性序列称为满足拓扑次序(Topological Order)的序列，简称拓扑序列。–《百度百科》

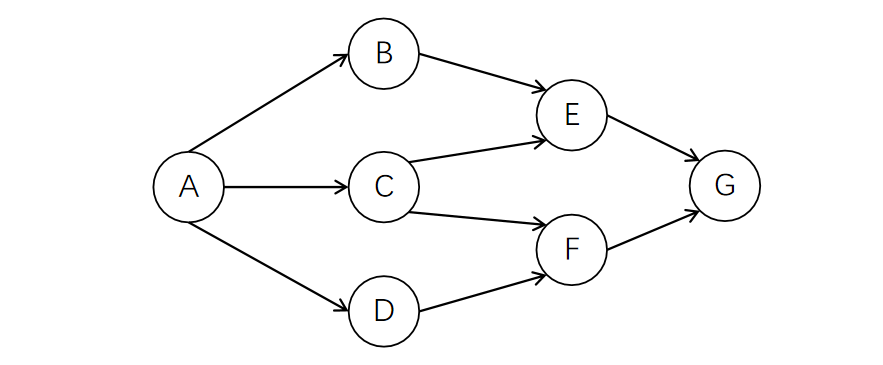
简单来讲，对于下面这张图，要想访问到B点，就必须先访问A点；要想访问E点，就必须先访问B点和C点…拓扑排序就是在保证各节点的优先级顺序不被打乱的前提下，遍历整张图的节点。拓扑排序形成的拓扑序列不一定只有一条。比如下面这张图的拓扑序列可以是：A->B->C->D->E->F->G，也可以是A->D->C->B->F->E->G。如果图的所有节点都遍历到了，那么这就是一张无环图；但如果有节点没有被遍历到，那么这张图一定存在环。

1.2 算法流程

拓扑排序的算法流程很简单：从图中找到一个入度为0的节点输出，然后删除这个顶点（包括依赖它的边）。重复此步骤，直到图中不存在入度为0的节点为止。

以前面的图为例。在起始状态下，图中入度为0的节点只有A，所以删除A节点

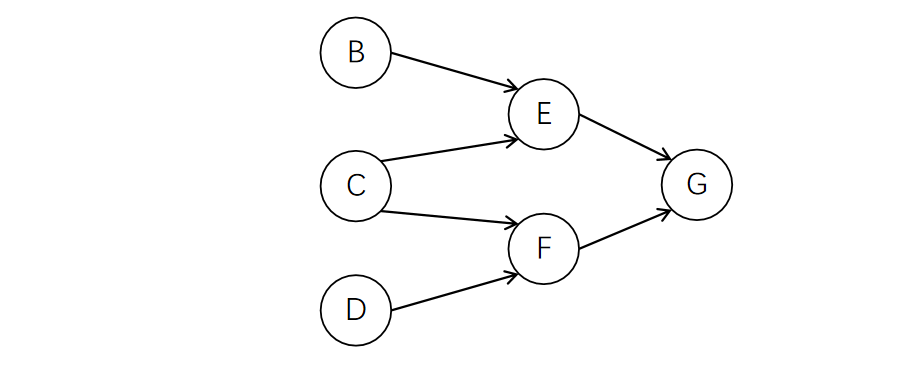
此时图中入度为0的节点有B、C、D。选择B点删除

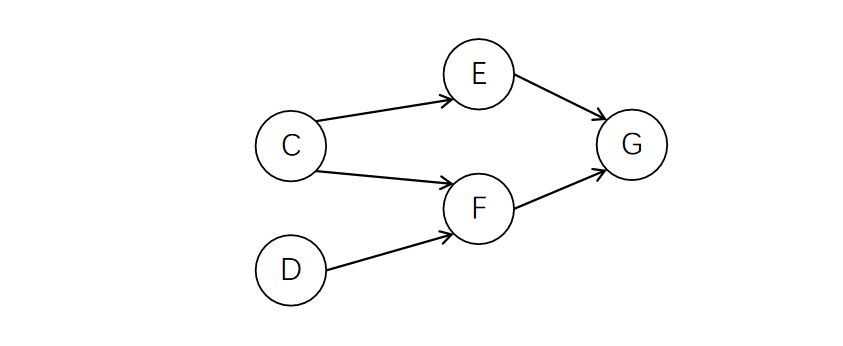
此时入度为0的点还剩下C、D。选择C删除

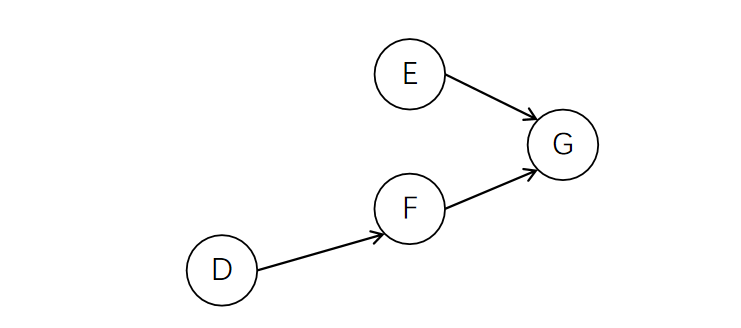
重复上述过程，直到没有入度为0的节点为止。

代码如下（这里的图采用邻接链表存储）

/// <summary>
/// 拓扑排序
/// </summary>
/// <param name="graph"></param>
private void Topological<T>(GraphByAdjacencyList<T> graph)
{
	Stack<int> stack = new Stack<int>(graph.Count);
	// 将入度为0的点加入栈
	for (int i = 0; i < graph.Count; i++)
	{
		if (graph.Nodes[i].inWeight == 0)
		{
			stack.Push(i);
		}
	}

	while (stack.Count > 0)
	{
		var nodeIndex = stack.Pop();
		Console.Write(graph.Nodes[nodeIndex].data+"->");
		// 遍历邻接链表
		var edge = graph.Nodes[nodeIndex].next;
		while (edge != null)
		{
			// 将入度都-1
			var index = edge.index;
			graph.Nodes[index].inWeight--;
			// 如果有入度为0的顶点,则入栈
			if (graph.Nodes[index].inWeight == 0)
			{
				stack.Push(index);
			}
			edge = edge.next;
		}
	}
}

二、关键路径

2.1 什么是关键路径

对于下面这张有向带权图，假设我们用边表示活动，边的权值表示活动的持续时间，顶点表示事件，则这张图就是一张表示活动的网，我们称之为AOE网。AOE网中没有入边的顶点为始点，没有出边的顶点为终点。

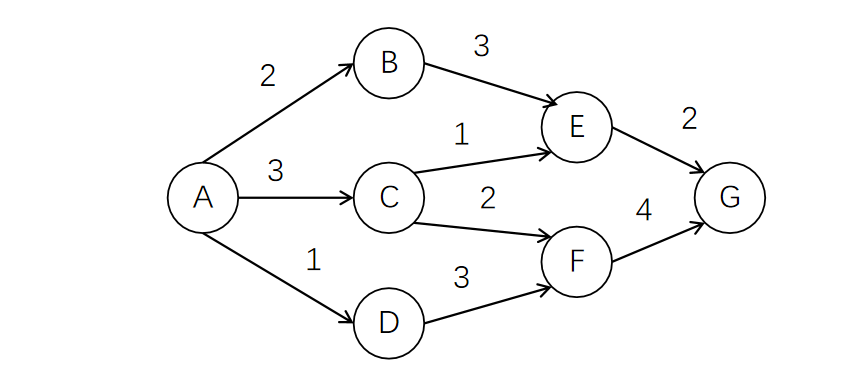
如果这张网表示的是一个工程，那么A点表示的就是工程的开始，G点表示的就是工程的结束。整个工程的耗时肯定不是所有边的权值总和，因为诸如A->B、A->C、A->D这类活动是可以并行进行的，所以整个工程的耗时取决于从始点到终点长度最大的路径。我们把路径上各个活动所持续的时间之和称为路径长度，从源点到汇点具有最大长度的路径叫关键路径，在关键路径上的活动叫关键活动。

至于如何找到这条关键路径就是接下来要讲的关键路径算法的任务了。

2.2 关键路径算法

我们先从最简单的开始入手，来看下面这张AOE网。

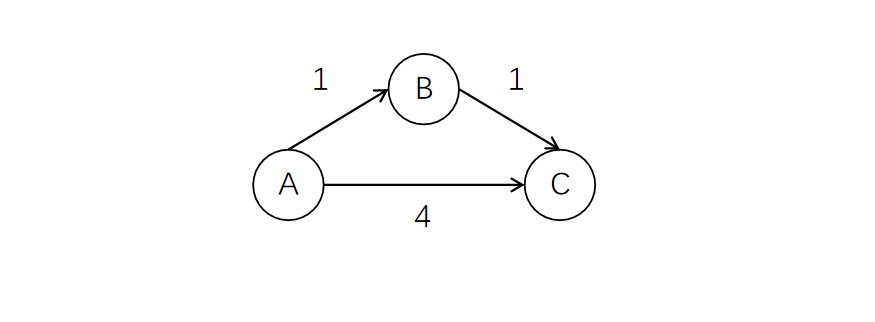
如果要完成这项工程，就需要A->B->C和A->C全部完成。对于A->B来说，因为A->C需要4天，所以即便自己晚几天开工也不迟。所以A->B的最早开始时间是0，也就是立即开工。最晚开始时间是3，因为还有给B->C留够时间。对于A->C来说，它的最早开始时间是0，最晚开始时间也是0，因为稍微晚一点开工就会造成工程整体延后。所以A->C就是关键活动。不难看出，对于任何一个活动，如果最早开始时间和最晚开始时间不相同，说明它不是关键活动。如果相同，则是关键活动。关键活动组成的路径就是关键路径。

为了求出活动（边）的最早和最晚开始时间，我们就需要先知道事件（顶点）的最早和最晚发生时间。所以我们先事先定义下面几个变量：

• 事件的最早发生时间etv（earliest time of vertex）
• 事件的最晚发生时间ltv（latest time of vertex）
• 活动的最早开工时间ete（earliest time of edge）
• 活动的最晚开工时间lte（latest time of edge）

接下来求事件最早发生时间。要求事件的最早发生时间，就需要弄清楚各事件间的依赖关系。比如开头这张图，假设我们要求G点的最早发生时间，就只需要知道E、F的最早发生时间$E_t、F_t$，然后在$E_t、F_t$的基础上加上活动的时间，再取它们之间的最大值即可。

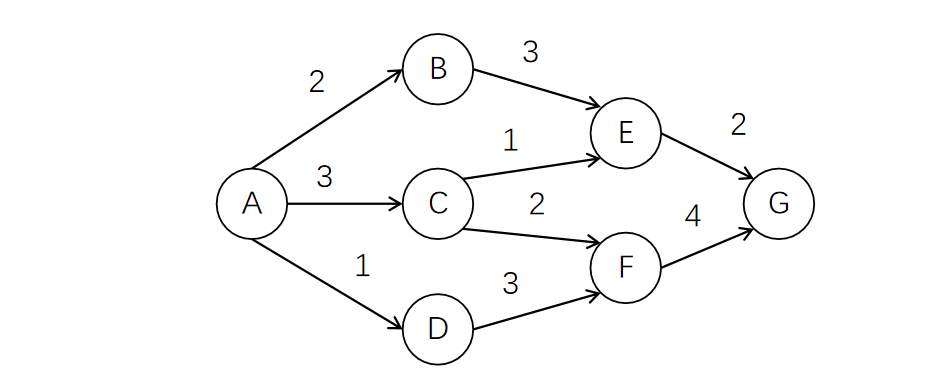
按照依赖关系遍历整张图，这正是前面拓扑排序的专长。所以我们只需要对之前拓扑排序的算法进行一点点改造，即可拿到我们想要的结果。

/// <summary>
/// 改进的拓扑排序
/// </summary>
/// <param name="graph"></param>
/// <param name="etv"></param>
private Stack<int> Topological2<T>(GraphByAdjacencyList<T> graph,out int[] etv)
{
	Stack<int> stack = new Stack<int>(graph.Count);
	// 将入度为0的点加入栈
	for (int i = 0; i < graph.Count; i++)
	{
		if (graph.Nodes[i].inWeight == 0)
		{
			stack.Push(i);
		}
	}
	// ..............新增Start.....................
	// 用来存储拓扑排序的结果并返回
	Stack<int> res = new Stack<int>(graph.Count);
	// 事件最早发生时间
	etv = new int[graph.Count];
	// ..............新增End.......................
	while (stack.Count > 0)
	{
		var nodeIndex = stack.Pop();
		// 遍历邻接链表
		var edge = graph.Nodes[nodeIndex].next;
		// ..............新增Start.....................
		// 将拓扑排序结果存入结果栈
		res.Push(nodeIndex);
		// ..............新增End.......................
		while (edge != null)
		{
			// 将入度都-1
			var index = edge.index;
			graph.Nodes[index].inWeight--;
			// 如果有入度为0的顶点,则入栈
			if (graph.Nodes[index].inWeight == 0)
			{
				stack.Push(index);
			}
			// ..............新增Start.....................
			// 如果(上一事件发生时间+活动持续时间)>当前记录的最早发生时间 则更新
			if (etv[nodeIndex] + edge.weight > etv[index])
			{
				etv[index] = etv[nodeIndex] + edge.weight;
			}
			// ..............新增End.......................
			edge = edge.next;
		}
	}
	return res;
}

有了事件最早发生时间，那么最晚发生时间也可以相应的求出来了。还是以这张图为例，假设我们要求的是C点的最晚发生时间，那就只需要先求出E、F的最晚发生时间，然后减去活动时间，取最小值即可。而E、F的最晚发生时间又可以由G点计算出。G点的最晚发生时间与最早发生时间是一致的（因为始点和终点一定在关键路径中），所以理论上这些点的最晚发生时间就都可以计算出来。

现在，图中的所有事件的最早发生时间和最晚发生时间我们都求出来了，接下来就是计算所有活动的最早开工时间和最晚开工时间。还是拿出前面那张图，对于C->E这项活动，它的最早开工时间与C的最早发生时间是一致的（事件刚发生就可以开工）。但它的最晚开工时间则取决于E的最晚发生时间（只要拖到E发生前做完就可以），即E的最晚开工时间 - 活动时间。

理解了这几个变量的计算方式，我们就可以开始写代码了

/// <summary>
/// 关键路径算法
/// </summary>
/// <param name="graph"></param>
private void CriticalPath<T>(GraphByAdjacencyList<T> graph)
{
	// 通过拓扑排序计算事件最早发生时间
	var topoStack = Topological2(graph, out int[] etv);
	// 定义事件最晚发生时间并初始化为终点的最早发生时间
	int[] ltv = new int[graph.Count];
	for (int i = 0; i < graph.Count; i++)
	{
		ltv[i] = etv[graph.Count - 1];
	}
	// 求事件最晚发生时间
	while (topoStack.Count > 0)
	{
		int nodeIndex = topoStack.Pop();
		// 遍历邻接链表
		var edge = graph.Nodes[nodeIndex].next;
		while (edge != null)
		{
			// 如果(下一个事件的最晚发生时间 - 活动时间) < 当前记录的最晚发生时间
			// 则意味着需要把工期提前
			if (ltv[edge.index] - edge.weight < ltv[nodeIndex] )
			{
				ltv[nodeIndex] = ltv[edge.index] - edge.weight;
			}
			edge = edge.next;
		}
	}

	for (int i = 0; i < graph.Count; i++)
	{
		// 遍历所有边
		var edge = graph.Nodes[i].next;
		while (edge != null)
		{
			// 最早开工时间 = 起始事件的最早发生时间
			int ete = etv[i];
			// 最晚开工时间 = 结束事件的最晚发生时间 - 活动时间
			int lte = ltv[edge.index] - edge.weight;
			// 最早开工时间 == 最晚开工时间,说明是关键活动
			if (ete == lte)
			{
				// 打印路径
				Console.Write($" {graph.Nodes[i].data}->{graph.Nodes[edge.index].data} ");
			}
			edge = edge.next;
		}
	}
}

三、参考资料

[1]. 《大话数据结构》