目录

 相交链表

环形链表

环形链表Ⅱ

---

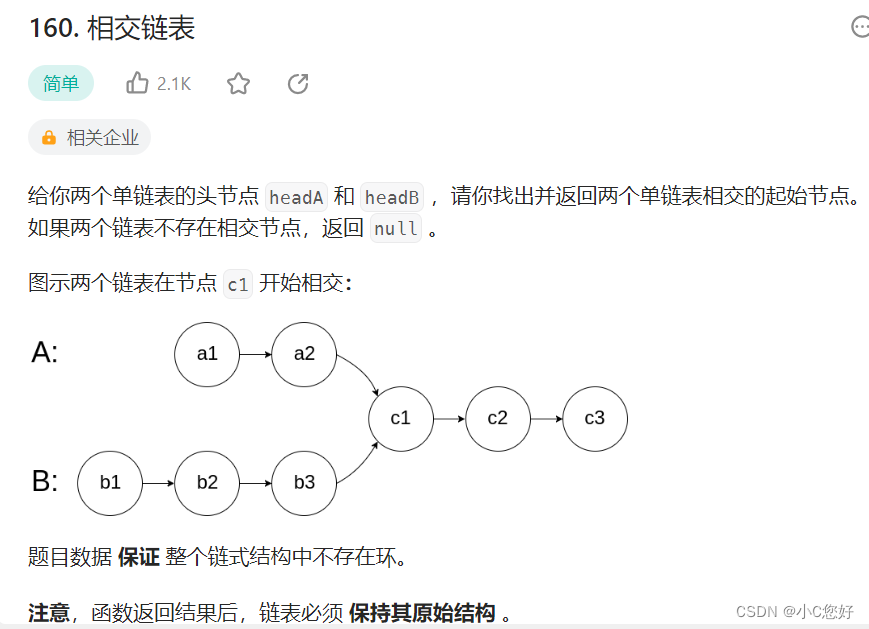
 相交链表

力扣

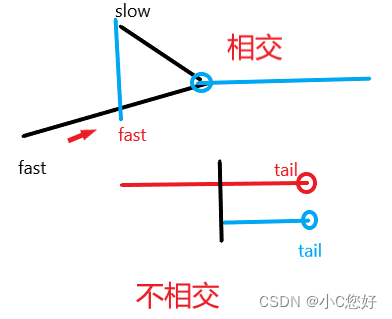
第一种思路：判断尾节点地址是否相同，时间复杂度为O(N^2)。

第二种思路：(节点对齐)记录两个链表节点个数，再根据节点差设置两个快慢指针进行next节点比对。时间复杂度O(N)(3N)。

注意：逆置链表达改变了单链表结构（相交时next指向两个节点），行不通。

struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB) {
    struct ListNode *curA = headA, *curB = headB;
    int lenA = 0,lenB = 0;//初始值设为0
    while(curA->next)
    {
            lenA++;
            curA = curA->next;
    }
    while(curB->next)
    {
            lenB++;
            curB = curB->next;
    }
    //尾不同
    if(curB != curA)
    
        return NULL;
        //尾相同
    int gap = abs(lenB - lenA);//绝对值absoulute
    //假设
    struct ListNode *longList = headA,*shortList = headB;
    if(lenA < lenB)
    {
        longList = headB;
        shortList = headA;
    }
    while(gap--)//长的先走gap步
    {
        longList = longList->next;
    }
    while(longList != shortList)
    {
        longList = longList->next;
        shortList = shortList->next;
    }
    return longList;
}

在计算长度的时候我们少计算了一个长度，但我们要求的是长度差，所以没有影响。 

当我们不知道哪个链表长的时候可以先假设其中一个链表大，另一个小，然后判断它们的长度做出假设失败的修改。

环形链表

力扣

这里有点像我们数学里的相遇问题，这里我们可以用快指针走两步，慢指针走一步的方式解决，最终它们终会相遇。

在进入环后，它们之间的距离每次缩小1，最终会相遇。进环后二者距离为N，假设环有M个节点，则N<M(等于时相遇)。所以slow最坏走了接近一圈的时候二者必然相遇。

bool hasCycle(struct ListNode *head) {
    struct ListNode* slow = head,*fast = head;
    while(fast && fast->next)//注意顺序
    {
        slow = slow->next;
        fast = fast->next->next;
         if(slow == fast)
             return true;
    }
   return false;
}

附加：为什么fast要走两步，slow只用走一步?

假设fast走三步，slow只走一步，假设进环后它们的距离是N,那么它的追击可能会出现两种情况。

N为偶数:N，N-2，N-4 .... 4，2，0

这种情况是可以追上的。 

N为奇数：N，N-2，N-4 .... 3，1，-1

当它们的距离为-1，即fast反超slow一步时，此时的距离为M-1(M为环的节点个数)

若M-1为偶数，则可以追上，若M为奇数，则永远追不上。

结论：当fast走2步以上时，需要判断奇偶决定是否可以追上，步步逼近必然能追上。

环形链表Ⅱ

力扣

这道题在前面那道题的基础上增加了返回入环的第一个结点(存在环时)。这里有一个前人总结的结论：当快慢指针相遇的时候的指针与头指针一起向后走,它们再次相遇的位置就是入环的位置。为什么呢？我们来解释一下。

 

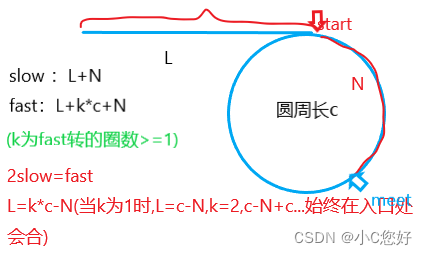
有几个注意点：当slow和fast相遇时,fast必然走了一圈以上(fast走的比slow快)，然后利用两倍关系，解出L的值，然后根据图示它们一起行动就会在起点相遇。

struct ListNode *detectCycle(struct ListNode *head) {
    struct ListNode* slow = head,*fast = head;
    while(fast && fast->next)//注意顺序
    {
        slow = slow->next;
        fast = fast->next->next;
         if(slow == fast)
            {
                struct ListNode* meet = slow;
                while(meet != head)
                {
                    meet = meet->next;
                    head = head->next;
                }
                return meet;
            }
    }
    return NULL;
}