数据结构与算法基础-学习-25-图之MST（最小代价生成树）之Prim（普利姆）算法

news2024/9/22 15:37:28

一、生成树概念

1、所有顶点均由边连接在一起，但不存在回路的图。

2、一个图可以有许多棵不同的生成树。

二、生成树特点

1、生成树的顶点个数与图的顶点个数相同。

2、生成树是图的极小连通子图，去掉一条边则非连通。

3、一个有n个顶点的连通图的生成树有n-1条边。

4、在生成树中再加一条边必然形成回路。

5、生成树中任意两个顶点间的路径是唯一的。

三、最小代价生成树（MST）

给定一个无向网，在该网的所有生成树中，使得各边权值之和最小的那颗生成树称为该网的最小生成树，也叫最小代价生成树。

四、MST实际中的应用

城市中需要铺设线路，怎么样铺设，使得成本低且覆盖所有城市。

五、Prim（普利姆）

1、宏定义

#define PARENT_INIT_VALUE             -1
#define LOWEST_WEIGHT_VALUE           0
#define LOWEST_EDGE_VERTEX_INIT_INDEX -1

2、结构体定义

//最小生成树
typedef struct MinimumSpanningTree
{
    VertexIndexType         StartIndex;//起始顶点
    VertexIndexType         EndIndex;  //结束顶点
    WeightType              Weight;    //起始顶点到结束顶点边上的权值
}MinimumSpanningTree;

typedef struct MstType
{
    MinimumSpanningTree* MstArray;
    WeightType           ArrayLen;
    WeightType           ArrayMaxLen;
}MstType;


//Prim
//普利姆算法适用于稠密图，所以我们这边用邻接矩阵实现。
typedef struct ShortestEdgeType
{
    VertexIndexType VertexIndex;
    WeightType      LowestWeight;
}ShortestEdgeType;

typedef struct ShortestEdgeArray
{
    ShortestEdgeType* Array;
    VertexIndexType   ArrayLen;
    VertexIndexType   ArrayMaxLen;
}ShortestEdgeArray;

3、函数定义

（1）InitShortestEdgeArray

VertexIndexType InitShortestEdgeArray(ShortestEdgeArray** SEA, AMGraph* AMG, VertexIndexType StartVertexIndex)
{
    JudgeAllNullPointer(SEA);
    JudgeAllNullPointer(AMG);

    *SEA                = (ShortestEdgeArray*)MyMalloc(sizeof(ShortestEdgeArray));
    (*SEA)->Array       = (ShortestEdgeType*)MyMalloc(sizeof(ShortestEdgeType) * (AMG->CurVertexNum));
    (*SEA)->ArrayLen    = 1;
    (*SEA)->ArrayMaxLen = AMG->CurVertexNum;

    VertexIndexType LowestEdgeVertexIndex = StartVertexIndex;
    VertexIndexType i;
    for(i = 0; i < AMG->CurVertexNum; i++)
    {
        (*SEA)->Array[i].VertexIndex  = StartVertexIndex;
        (*SEA)->Array[i].LowestWeight = AMG->ArcArray[StartVertexIndex][i];
        if(AMG->ArcArray[StartVertexIndex][LowestEdgeVertexIndex] > AMG->ArcArray[StartVertexIndex][i])
        {
            LowestEdgeVertexIndex = i;
        }
    }
    (*SEA)->Array[StartVertexIndex].LowestWeight = LOWEST_WEIGHT_VALUE;
    PrintfShortestEdgeArray(*SEA);
    Log("Init ShortestEdgeArray OK\n",Debug);
    return LowestEdgeVertexIndex;
}

初始化时需要放入起始结点的索引，返回最小边结束顶点的索引号。

参数名描述
SEA需要初始化的最短边数组。
AMG邻接矩阵图。
StartVertexIndex起始顶点索引号。

（2）UpdateShortestEdgeArray

VertexIndexType UpdateShortestEdgeArray(ShortestEdgeArray* SEA, AMGraph* AMG, VertexIndexType UpdateVertexIndex)
{
    JudgeAllNullPointer(SEA);
    JudgeAllNullPointer(AMG);

    VertexIndexType LowestEdgeVertexIndex = LOWEST_EDGE_VERTEX_INIT_INDEX;
    VertexIndexType i;

    for(i = 0; i < SEA->ArrayMaxLen; i++)
    {
       if(SEA->Array[i].LowestWeight != LOWEST_WEIGHT_VALUE && i != UpdateVertexIndex)//权值不为0，表示没包含的点，可以操作，进入此判断。
       {
           if(SEA->Array[i].LowestWeight > AMG->ArcArray[UpdateVertexIndex][i])//最小边数组的权值小于邻接矩阵中的权值，这时需要更新，进入此判断。
           {
               SEA->Array[i].VertexIndex  = UpdateVertexIndex;
               SEA->Array[i].LowestWeight = AMG->ArcArray[UpdateVertexIndex][i];
           }
           LowestEdgeVertexIndex = i;
           break;
       }
    }

    for(i = LowestEdgeVertexIndex + 1; i < SEA->ArrayMaxLen; i++)
    {
       if(SEA->Array[i].LowestWeight != LOWEST_WEIGHT_VALUE && i != UpdateVertexIndex)//权值不为0，表示没包含的点，可以操作，进入此判断。
       {
           if(SEA->Array[i].LowestWeight > AMG->ArcArray[UpdateVertexIndex][i])//最小边数组的权值小于邻接矩阵中的权值，这时需要更新，进入此判断。
           {
               SEA->Array[i].VertexIndex  = UpdateVertexIndex;
               SEA->Array[i].LowestWeight = AMG->ArcArray[UpdateVertexIndex][i];
           }
           if(SEA->Array[i].LowestWeight < SEA->Array[LowestEdgeVertexIndex].LowestWeight)//找出最小权值的顶点索引号。
           {
               LowestEdgeVertexIndex = i;
           }         
       } 
    }
    SEA->Array[UpdateVertexIndex].LowestWeight = LOWEST_WEIGHT_VALUE;
    SEA->ArrayLen++;
    PrintfShortestEdgeArray(SEA);
    return LowestEdgeVertexIndex;
}

根据邻接矩阵AMG和需要更新的顶点索引UpdateVertexIndex，更新SEA最小边数组。
返回最小边结束顶点的索引号。

参数名描述
SEA最短边数组。
AMG邻接矩阵图。
UpdateVertexIndex需要更新的顶点索引号。

（3）DestroyShortestEdgeArray

Status DestroyShortestEdgeArray(ShortestEdgeArray** SEA)
{
    JudgeAllNullPointer(SEA);
    JudgeAllNullPointer(*SEA);

    free((*SEA)->Array);
    (*SEA)->Array       = NULL;
    (*SEA)->ArrayLen    = 0;
    (*SEA)->ArrayMaxLen = 0;
    free(*SEA);
    *SEA                = NULL;
    Log("Destroy ShortestEdgeArray OK\n",Debug);
    return SuccessFlag;
}

销毁SEA最短边数组。

参数名描述
SEA需要销毁的最短边数组。

（4）PrimMST

Status PrimMST(AMGraph* AMG, MstType* MST, VertexIndexType StartVertexIndex)
{
    JudgeAllNullPointer(AMG);
    JudgeAllNullPointer(MST);

    ShortestEdgeArray* SEA                   = NULL;
    VertexIndexType    LowestEdgeVertexIndex = InitShortestEdgeArray(&SEA, AMG, StartVertexIndex);
    PushMST(MST, SEA->Array[LowestEdgeVertexIndex].VertexIndex, LowestEdgeVertexIndex, SEA->Array[LowestEdgeVertexIndex].LowestWeight);
    printf("LowestEdgeVertexIndex : %d\n",LowestEdgeVertexIndex);
    while(MST->ArrayMaxLen > MST->ArrayLen)
    {
        LowestEdgeVertexIndex = UpdateShortestEdgeArray(SEA, AMG, LowestEdgeVertexIndex);
        printf("LowestEdgeVertexIndex : %d\n",LowestEdgeVertexIndex);
        PushMST(MST, SEA->Array[LowestEdgeVertexIndex].VertexIndex, LowestEdgeVertexIndex, SEA->Array[LowestEdgeVertexIndex].LowestWeight);
    }

    DestroyShortestEdgeArray(&SEA);
    Log("Prim Create MST OK\n",Info);
    return SuccessFlag;
}

初始化时需要放入起始结点的索引，返回最小边结束顶点的索引号。

参数名描述
SEA需要初始化的最短边数组。
MST最小代价生产树。
StartVertexIndex起始顶点索引号。

（5）InitMST

Status InitMST(MstType** MST, VertexIndexType VertexNum)
{
    JudgeAllNullPointer(MST);

    *MST                = (MstType*)MyMalloc(sizeof(MstType));
    (*MST)->MstArray    = (MinimumSpanningTree*)MyMalloc(sizeof(MinimumSpanningTree) * (VertexNum - 1));
    (*MST)->ArrayLen    = 0;
    (*MST)->ArrayMaxLen = VertexNum - 1;

    return SuccessFlag;
}

初始化MST。

参数名描述
MST最小代价生产树。
VertexNum图的顶点总个数。

（6）DestroyMST

Status DestroyMST(MstType** MST)
{
    JudgeAllNullPointer(MST);
    JudgeAllNullPointer(*MST);

    free((*MST)->MstArray);
    (*MST)->MstArray    = NULL;
    (*MST)->ArrayLen    = 0;
    (*MST)->ArrayMaxLen = 0;
    free(*MST);
    *MST                = NULL;

    return SuccessFlag;
}

销毁MST。

参数名描述
MST最小代价生产树。

 （7）PushMST

Status PushMST(MstType* MST, VertexIndexType StartIndex, VertexIndexType EndIndex, WeightType Weight)
{
    JudgeAllNullPointer(MST);
    if(MST->ArrayMaxLen == MST->ArrayLen)
    {
        Log("MST Array Is Full, Can't Push Data!",Error);
        exit(ExceptionExitFlag);
    }

    MST->MstArray[MST->ArrayLen].StartIndex = StartIndex;
    MST->MstArray[MST->ArrayLen].EndIndex   = EndIndex;
    MST->MstArray[MST->ArrayLen].Weight     = Weight;
    MST->ArrayLen++;

    return SuccessFlag;
}

压数据到MST中。

参数名描述
MST最小代价生产树。
StartIndex边的顶点起始索引号。
EndIndex边的顶点结束索引号。
Weight边的权值。

4、实现思路

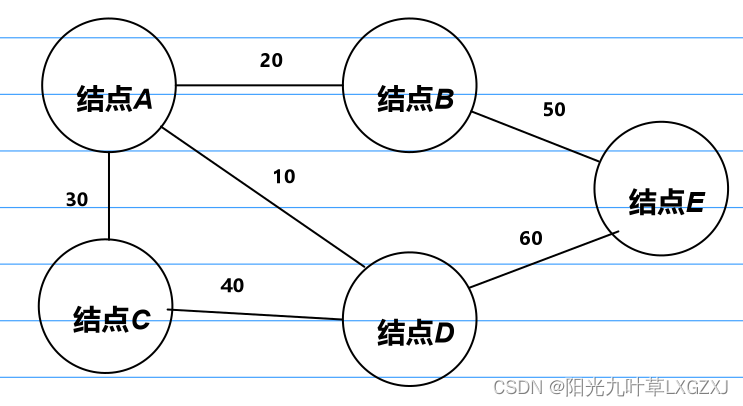
我们还是以之前的图为例，其实是偷个小懒。

由于Prim算法适用于稠密图，所以结合邻接矩阵图实现这个算法。对应邻接矩阵图如下：

[2023-6]--[ Debug ]--Printf AMGraph                     :
VertexArray    : [A ,B ,C ,D ,E ]
ArcArray       :
[32767 ,20    ,30    ,10    ,32767 ]
[20    ,32767 ,32767 ,32767 ,50    ]
[30    ,32767 ,32767 ,40    ,32767 ]
[10    ,32767 ,40    ,32767 ,60    ]
[32767 ,50    ,32767 ,60    ,32767 ]
CurVertexNum   : 5
CurArcNum      : 12

我们还需要维护一个最短边数组，里面记录了各个点到各个点的最小权值。例如我们从A点出发，也就是索引号为0的点出发，初始化最短边数组。

[2023-6]--[ Debug ]--Printf ShortestEdgeArray
{(0,0),(0,20),(0,30),(0,10),(0,32767)}
ArrayLen    : 1
ArrayMaxLen : 5

（1）(0,0)第一个0表示起始节点的索引号，第二个0表示权值，如果为0则表示顶点已被访问。(0,0)在最短边数组的0号位，这个0为结束节点索引号，意思表示A点到A点，A点被访问。

（2）(0,20)第一个0表示起始节点的索引号，第二个20表示权值。(0,20)在最短边数组的1号位，这个1为结束节点索引号，意思表示A点到B点，权值为20。

（3）(0,30)第一个0表示起始节点的索引号，第二个30表示权值。(0,30)在最短边数组的2号位，这个2为结束节点索引号，意思表示A点到C点，权值为30。

（4）(0,10)第一个0表示起始节点的索引号，第二个10表示权值。(0,10)在最短边数组的3号位，这个3为结束节点索引号，意思表示A点到D点，权值为10。

（5）(0,32767)第一个0表示起始节点的索引号，第二个32767表示无穷大。(0,32767)在最短边数组的4号位，这个4为结束节点索引号，意思表示A点不能到达E点。

LowestEdgeVertexIndex : 3

后四个权值进行比较发现(0,10)的权值最小，A节点已被访问不需要比较，它在最短边数组的3号位，表示D节点被使用。

我们进行更新最短边数组，这里和邻接矩阵的3号位的权值进行比较。

邻接矩阵3号位：

[10    ,32767 ,40    ,32767 ,60    ]

（1）0号位的A节点已使用，不用对比。

（2）1号位的B节点，A->B权值为20，比3号位的D节点D->B权值为32767小，还是最短的，不更新。

（3）2号位的C节点，A->C权值为30，比3号位的D节点D->C权值为40小，还是最短的，不更新。

（4）3号位的D节点已使用，不用对比。

（5）4号位的E节点，A->E权值为32767，比3号位的D节点D->E权值为60大，更新。

变化后的最短边数组如下：

[2023-6]--[ Debug ]--Printf ShortestEdgeArray
{(0,0),(0,20),(0,30),(0,0),(3,60)}
ArrayLen    : 2
ArrayMaxLen : 5

(0,20),(0,30),(3,60)的权值进行比较，发现最小的是(0,20)，返回索引号。

LowestEdgeVertexIndex : 1

1号索引表示B节点已经被使用。

邻接矩阵1号位：

[20    ,32767 ,32767 ,32767 ,50    ]

（1）0号位的A节点已使用，不用对比。

（2）1号位的B节点已使用，不用对比。

（3）2号位的C节点，A->C权值为30，比1号位的B节点B->C权值为32767小，还是最短的，不更新。

（4）3号位的D节点已使用，不用对比。

（5）4号位的E节点，D->E权值为60，比1号位的B节点B->E权值为50大，更新。

更新最短边数组：

[2023-6]--[ Debug ]--Printf ShortestEdgeArray
{(0,0),(0,0),(0,30),(0,0),(1,50)}
ArrayLen    : 3
ArrayMaxLen : 5

（0，30）为最小的权值，对应的索引号为2，表示C节点。

邻接矩阵2号位：

[30    ,32767 ,32767 ,40    ,32767 ]

（1）0号位的A节点已使用，不用对比。

（2）1号位的B节点已使用，不用对比。

 （3）2号位的C节点已使用，不用对比。

（4）3号位的D节点已使用，不用对比。

（5）4号位的E节点，B->E权值为50，比2号位的C节点C->E权值为32767小，不更新。

[2023-6]--[ Debug ]--Printf ShortestEdgeArray
{(0,0),(0,0),(0,0),(0,0),(1,50)}
ArrayLen    : 4
ArrayMaxLen : 5

一个有n个顶点的连通图的生成树有n-1条边。

五个顶点，我们已经拿到四条边，可以形成MST，退出程序。

六、Linux环境代码测试

[gbase@czg2 Graph]$ make
gcc -Wall -Wextra -O3 ../Log/Log.c ../PublicFunction/PublicFunction.c ../PublicFunction/SqQueue/SqQueue.c Graph.c MinimumSpanningTree.c main.c -o TestGraph -I ../Log/ -I ../PublicFunction/ -I ../Select/ -I ../PublicFunction/SqQueue/
[gbase@czg2 Graph]$ ./TestGraph 
[2023-6]--[ Info  ]--Create Net Data                    : OK
[2023-6]--[ Info  ]--Create Undirection Net Use AMGraph : OK
[2023-6]--[ Debug ]--Printf AMGraph                     :
VertexArray    : [A ,B ,C ,D ,E ]
ArcArray       :
[32767 ,20    ,30    ,10    ,32767 ]
[20    ,32767 ,32767 ,32767 ,50    ]
[30    ,32767 ,32767 ,40    ,32767 ]
[10    ,32767 ,40    ,32767 ,60    ]
[32767 ,50    ,32767 ,60    ,32767 ]
CurVertexNum   : 5
CurArcNum      : 12
[2023-6]--[ Info  ]--Create Undirection Net Use AGraph  : OK
[2023-6]--[ Debug ]--Printf AGraph                      :
A : [(2, 30, 0x1ff28b0),(1, 20, 0x1ff2870),(3, 10, (nil))]
B : [(4, 50, 0x1ff28d0),(0, 20, (nil))]
C : [(3, 40, 0x1ff2910),(0, 30, (nil))]
D : [(4, 60, 0x1ff2950),(2, 40, 0x1ff2890),(0, 10, (nil))]
E : [(3, 60, 0x1ff2990),(1, 50, (nil))]
VertexNum      : 5
ArcNum         : 12
[2023-6]--[ Debug ]--Traverse Use AMGraph               : [4 ,1 ,0 ,2 ,3 ]
[2023-6]--[ Debug ]--Traverse Use AGraph                : [4 ,3 ,2 ,0 ,1 ]
[2023-6]--[ Debug ]--Init SqQueue Normal
[2023-6]--[ Debug ]--Enter SqQueue Normal
[2023-6]--[ Debug ]--Leave SqQueue Normal
[2023-6]--[ Debug ]--Enter SqQueue Normal
[2023-6]--[ Debug ]--Enter SqQueue Normal
[2023-6]--[ Debug ]--Leave SqQueue Normal
[2023-6]--[ Debug ]--Enter SqQueue Normal
[2023-6]--[ Debug ]--Leave SqQueue Normal
[2023-6]--[ Debug ]--Enter SqQueue Normal
[2023-6]--[ Debug ]--Destroy SqQueue Normal
[2023-6]--[ Debug ]--Breadth First Search Use AMGraph OK
[2023-6]--[ Debug ]--Traverse Use AMGraph               : [4 ,1 ,3 ,0 ,2 ]
[2023-6]--[ Debug ]--Init SqQueue Normal
[2023-6]--[ Debug ]--Enter SqQueue Normal
[2023-6]--[ Debug ]--Leave SqQueue Normal
[2023-6]--[ Debug ]--Enter SqQueue Normal
[2023-6]--[ Debug ]--Enter SqQueue Normal
[2023-6]--[ Debug ]--Leave SqQueue Normal
[2023-6]--[ Debug ]--Enter SqQueue Normal
[2023-6]--[ Debug ]--Enter SqQueue Normal
[2023-6]--[ Debug ]--Destroy SqQueue Normal
[2023-6]--[ Debug ]--Breadth First Search Use AGraph OK
[2023-6]--[ Debug ]--Traverse Use AGraph                : [4 ,3 ,1 ,2 ,0 ]
[2023-6]--[ Debug ]--Printf ShortestEdgeArray
{(0,0),(0,20),(0,30),(0,10),(0,32767)}
ArrayLen    : 1
ArrayMaxLen : 5
[2023-6]--[ Debug ]--Init ShortestEdgeArray OK
LowestEdgeVertexIndex : 3
[2023-6]--[ Debug ]--Printf ShortestEdgeArray
{(0,0),(0,20),(0,30),(0,0),(3,60)}
ArrayLen    : 2
ArrayMaxLen : 5
LowestEdgeVertexIndex : 1
[2023-6]--[ Debug ]--Printf ShortestEdgeArray
{(0,0),(0,0),(0,30),(0,0),(1,50)}
ArrayLen    : 3
ArrayMaxLen : 5
LowestEdgeVertexIndex : 2
[2023-6]--[ Debug ]--Printf ShortestEdgeArray
{(0,0),(0,0),(0,0),(0,0),(1,50)}
ArrayLen    : 4
ArrayMaxLen : 5
LowestEdgeVertexIndex : 4
[2023-6]--[ Debug ]--Destroy ShortestEdgeArray OK
[2023-6]--[ Info  ]--Prim Create MST OK
[2023-6]--[ Debug ]--Printf MST
{ (0,3,10),(0,1,20),(0,2,30),(1,4,50)}
[2023-6]--[ Info  ]--Destroy Net Data                   : OK
[2023-6]--[ Info  ]--Destroy Undirection Net Use AMGraph: OK
[2023-6]--[ Info  ]--Destroy Undirection Net Use AGraph : OK

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/697591.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

stm32f103c8t6移植U8g2

stm32f103c8t6移植U8g2

U8g2代码下载&#xff1a; https://github.com/olikraus/u8g2 1&#xff0c;准备一个正常运行的KEIL5 MDK模板 2&#xff0c;下载u8g2的源码和 u8g2的STM32实例模板 源码: https://github.com/olikraus/u8g2 STM32实例模板: https://github.com/nikola-v/u8g2_template_stm32f…
阅读更多...
100天精通Golang（基础入门篇）——第11天：深入解析Go语言中的切片(Slice)及常用函数应用

100天精通Golang（基础入门篇）——第11天：深入解析Go语言中的切片(Slice)及常用函数应用

&#x1f337; 博主 libin9iOak带您 Go to Golang Language.✨ &#x1f984; 个人主页——libin9iOak的博客&#x1f390; &#x1f433; 《面试题大全》 文章图文并茂&#x1f995;生动形象&#x1f996;简单易学&#xff01;欢迎大家来踩踩~&#x1f33a; &#x1f30a; 《I…
阅读更多...
期望最大化注意力网络 EMANet

期望最大化注意力网络 EMANet

论文&#xff1a;Expectation-Maximization Attention Networks for Semantic Segmentation Github&#xff1a;https://github.com/XiaLiPKU/EMANet ICCV2019 oral 论文提出的期望最大化注意力机制Expectation- Maximization Attention (EMA)&#xff0c;摒弃了在全图上计算注…
阅读更多...
再述时序约束

再述时序约束

再述时序约束 一、为什么要加时序约束&#xff1f;二、时序分析是什么&#xff1f;三、时序分析的一些基本概念三、 时序分析的一些基本公式 一、为什么要加时序约束&#xff1f; 一次笔者在调试HDMI输出彩条&#xff0c;出现彩条时有时无现象&#xff0c;笔者视频输出芯片的驱…
阅读更多...
leecode-数组多数-摩尔投票法

leecode-数组多数-摩尔投票法

题目 题目 分析 最开始思路&#xff1a;排序&#xff0c;然后取nums[n/2]&#xff0c;但是时间复杂度不过关。 摩尔投票法&#xff0c;学到了&#xff01; 代码 class Solution { public:int majorityElement(vector<int>& nums) {//摩尔投票int cnt0;int targ…
阅读更多...
计算机二级c语言题库

计算机二级c语言题库

计算机C语言二级考试&#xff08;60道程序设计&#xff09; 第1道 请编写一个函数fun,它的功能是:将ss所指字符串中所有下标为奇数位置上的字母转换成大写&#xff08;若该位置上不是字母&#xff0c;则不转换&#xff09;。 例如&#xff0c;若输入"abc4EFG"&…
阅读更多...
OpenCV学习笔记 | ROI区域选择提取 | Python

OpenCV学习笔记 | ROI区域选择提取 | Python

摘要 ROI区域是指图像中我们感兴趣的特定区域&#xff0c;OpenCV提供了一些函数来选择和提取ROI区域&#xff0c;我们可以使用OpenCV的鼠标事件绑定函数&#xff0c;然后通过鼠标操作在图像上绘制一个矩形框&#xff0c;该矩形框即为ROI区域。本文将介绍代码的实现以及四个主要…
阅读更多...
opencv编译

opencv编译

文章目录 一、编译前工作二、编译安装1、Windows2、Linux 一、编译前工作 进入下载页面https://github.com/opencv/opencv&#xff0c;下载指定.tar.gz源码包&#xff0c;例如&#xff1a;opencv-4.7.0.tar.gz。解压到指定目录。 二、编译安装 opencv构建时&#xff0c;需要…
阅读更多...
使用docker搭建hadoop集群

使用docker搭建hadoop集群

1.下载安装docker 2.启动docker 3.配置docker镜像 4.获取hadoop镜像 5.拉取hadoop镜像 6.运行容器 7.进入容器 8.配置免密 9.格式化节点 10.启动节点 11.查看节点信息 (img-CBr9VbGk-1687962511910)] 11.查看节点信息
阅读更多...
javascript原型、原型链、继承详解

javascript原型、原型链、继承详解

一、原型和原型链的基本概念 在JavaScript中&#xff0c;每个对象都有一个原型对象&#xff08;prototype&#xff09;。原型对象就是一个普通的对象&#xff0c;在创建新对象时&#xff0c;可以将该对象作为新对象的原型。原型对象可以包含共享的属性和方法&#xff0c;这些属…
阅读更多...
Appium自动化-ADB连接手机提示unauthorized

Appium自动化-ADB连接手机提示unauthorized

目录 开头&#xff1a; 问题&#xff1a; 调研&#xff1a; 重启大法 终极大法 总结&#xff1a; 开头&#xff1a; 当使用ADB&#xff08;Android Debug Bridge&#xff09;连接手机时&#xff0c;如果提示"unauthorized"&#xff08;未授权&#xff09;错误&a…
阅读更多...
javaee HttpSessionListener监听器统计在线人数

javaee HttpSessionListener监听器统计在线人数

先创建ServletContextListener 在全局对象application中设置count属性 package com.yyy.listener;import java.util.ArrayList;import javax.servlet.ServletContext; import javax.servlet.ServletContextEvent; import javax.servlet.ServletContextListener; import javax…
阅读更多...
易基因｜表观遗传学与脑卒中：DNA甲基化的作用及衰老对血脑屏障修复的影响

易基因｜表观遗传学与脑卒中：DNA甲基化的作用及衰老对血脑屏障修复的影响

大家好&#xff0c;这里是专注表观组学十余年&#xff0c;领跑多组学科研服务的易基因。 脑卒中&#xff08;俗称中风&#xff09;是导致死亡和长期残疾的主要原因&#xff0c;尤其是对于老龄人来说。脑卒中的平均生存时间为6-7年&#xff0c;许多患者存在身体残疾和晚期认知功…
阅读更多...
技术岗/算法岗面试如何准备？5000字长文、6个角度以2023秋招经历分享面试经验

技术岗/算法岗面试如何准备？5000字长文、6个角度以2023秋招经历分享面试经验

技术岗/算法岗面试流程是什么样的&#xff1f;技术面都干什么&#xff1f;Coding 机试如何准备&#xff1f;技术面考察哪些知识&#xff0c;如何准备&#xff1f;项目八股如何准备&#xff1f;简历要注意什么&#xff1f;怎么做&#xff1f; 大家好&#xff0c;我是卷了又没卷…
阅读更多...
uniapp 适配全面屏

uniapp 适配全面屏

1、manifest.json 文件修改 app-plus 下 添加 "safearea": {"background": "#00000000","bottom": {"offset": "auto"}},2、部分页面设置全屏&#xff08;登录页面&#xff09; methods: {//设置页面全屏onShow(…
阅读更多...
SpringBoot（二）starter介绍

SpringBoot（二）starter介绍

做Java后端的同学可能都知道&#xff0c;在SpringBoot诞生之前&#xff0c;还有传统的Spring。这种Spring项目想要运行&#xff0c;需要导入各种依赖&#xff0c;而且还要在 XML 配置文件中一顿配置&#xff0c;非常痛苦。但通过上篇博客我们可以看到&#xff0c;SpringBoot项目…
阅读更多...
事务与隔离级别

事务与隔离级别

事务四要素 原子性&#xff08;Atomicity&#xff09;&#xff1a;要么全部完成&#xff0c;要么全部不完成&#xff1b;一致性&#xff08;Consistency&#xff09;&#xff1a;一个事务单元需要提交之后才会被其他事务可见&#xff1b;隔离性&#xff08;Isolation&#xff…
阅读更多...
azure databricks因为notebook 日志打多或者打印图片太多，往下拉卡死怎么处理

azure databricks因为notebook 日志打多或者打印图片太多，往下拉卡死怎么处理

1、同事碰到个问题&#xff0c;databricks 页面卡死不动了 2、我。。。。。。。。测试了下搞不定&#xff0c;找azure的工程师&#xff0c;特此笔记如下图 !](https://img-blog.csdnimg.cn/5db9756d0e224d15a9a607561b47591f.png)
阅读更多...
怎样自定义starter模块和使用

怎样自定义starter模块和使用

一、 自定义Starter模块 在实际开发中&#xff0c;经常会定义一些公共组件&#xff0c;提供给各个项目团队使用。而在SpringBoot的项目中&#xff0c;一般会将这些公共组件封装为SpringBoot的starter(起步依赖)。 1.1实例–阿里云OSS的配置 前言&#xff1a;我们在使用阿里云…
阅读更多...
windows下MySQL 5.7.31的安装

windows下MySQL 5.7.31的安装

文章目录 安装步骤检查是否安装成功配置环境变量 安装步骤 双击安装包mysql-installer-community-5.7.31.0.msi选择自定义安装“custom”&#xff0c;点击next “Developer Default”是开发者默认“Server only”仅作为服务器安装“Clientonly”仅作为客户端安装“Full”是完…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023