论文:Expectation-Maximization Attention Networks for Semantic Segmentation
Github:https://github.com/XiaLiPKU/EMANet
ICCV2019 oral
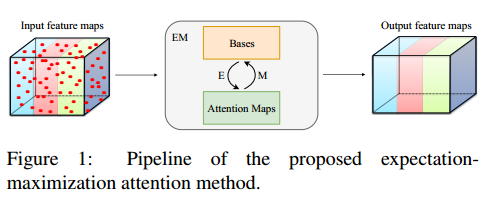
论文提出的期望最大化注意力机制Expectation- Maximization Attention (EMA),摒弃了在全图上计算注意力图的流程,转而通过期望最大化(EM)算法迭代出一组紧凑的基,在这组基上运行注意力机制,从而大大降低了复杂度。其中,E步更新注意力图,M步更新这组基。E、M交替执行,收敛之后用来重建特征图。本文把这一机制嵌入网络中,构造出轻量且易实现的EMA Unit。其作为语义分割头,在多个数据集PASCAL VOC, PASCAL Context,COCO Stuff取得了较高的精度。
主要贡献:
- 本文首次提出使用期望最大化方法重新定义attention算法,通过该方法可以学习到更加紧致的基并且大大的减少了计算复杂度。
- 将整个期望最大化的迭代过程通过神经网络实现,并且提出了Expectation maximization Attention Unit (EMAU)模块,所有神经网络都可以很方便的复用该模块。
- 在PASCAL VOC, PASCAL Context,COCO Stuff3个数据集上取得了state-of-the-art的效果。
期望最大化算法:
期望最大化(EM)算法旨在为隐变量模型寻找最大似然解。
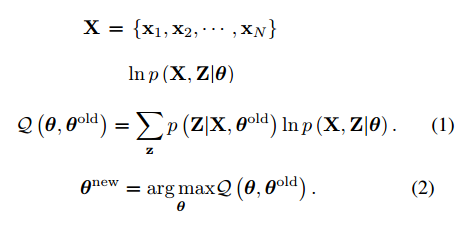
X表示观测数据,Z表示隐变量空间,每一个数据x都有相应的隐变量与其对应,{X,Z}称为完整的数据,其极大似然估计就是lnp(X,Z|q),q表示模型的参数。
期望最大化算法分为E步和M步两个步骤。E步根据qold计算隐变量Z的后验分布,并以之寻找完整数据的似然Q。M步通过最大化似然函数来更新参数得到qnew。
EM算法被证明会收敛到局部最大值处,且迭代过程完整数据似然值单调递增。
高斯混合模型:

高斯混合模型(GMM)是EM算法的一个范例,它把数据用多个高斯分布拟合。其qk即为第k个高斯分布的参数uk,åk,隐变量znk为第k个高斯分布对第n数据点的“责任”。E步更新“责任”,M步更新高斯参数。在实际应用中,åk经常被简化为I。
非局部网络:
非局部网络(Nonlocal)率先将自注意力机制使用在计算机视觉任务中。其核心算子是:

Xi表示位置i处的特征向量,f(Xi,Xj)表示广义的核函数,C(X) 是归一化系数, 它将第i个像素的特征Xi更新为其他所有像素特征经过g变换之后的加权平均yi。权重通过归一化后的核函数计算,表征两个像素之间的相关度。
非局部网络(Nonlocal)存在2个缺点,第一,基数目巨大,且存在大量信息冗余。第二,计算量大,内存消耗也大。
期望最大化注意力机制:
期望最大化注意力机制由Aer,Am,Ar三部分组成,前两者分别对应EM算法的E步和M步。
假定输入的特征图为XRN*C,基初始值为U
RK*C ,Ae估计隐变量Z
RN*K,即每个基对像素的权责。具体地,第k个基对第n个像素的权责可以计算为:

在这里,内核K(a,b)可以有多种选择。我们选择exp(a⊤b)的形式。在实现中,可以用如下的方式实现:
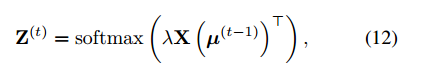
其中,l作为超参数来控制Z的分布。
Am 步更新基u,为了保证u和X处在同一表征空间内,此处u被计算作X的加权平均。具体地,第k个基被更新为:
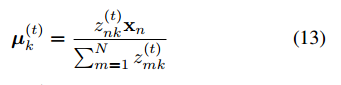
值得注意的是,如果∞,则公式(5)中{zn1,zn2,……znk}会变成一组one-hot编码。在这种情形下,每个像素仅由一个基负责,而基被更新为其所负责的像素的均值,这便是标准的K-means算法。
AE和AM交替执行T步。此后,近似收敛的u和Z便可以被用来对X进行重估计得X~。

X~相比于X,具有低秩的特性。从下图中可看出,其在保持类间差异的同时,类别内部差异得到缩小。从图像角度来看,起到了类似保边滤波的效果。
综上,EMA在获得低秩重构特性的同时,将复杂度从Nonlocal的O(N2)降低至O(NKT)。实验中,EMA仅需3步就可达到近似收敛,因此T作为一个小常数,可以被省去。至此,EMA复杂度仅为O(NK)。考虑到K<<N,其复杂度得到显著的降低。
期望最大注意力模块EMAU:

Expectation maximization Attention Unit (EMAU) 结构如上图所示。除了核心的EMA之外,两个1×1卷积分别放置于EMA前后。前者将输入的值域从R+映射到R;后者将X~映射到X的残差空间。囊括进两个卷积的额外负荷,EMAU的FLOPs仅相当于同样输入输出大小时3×3卷积的1/3,参数量仅为2C2+KC。
对于EM算法而言,参数的初始化会影响到最终收敛时的效果。对于深度网络训练过程中的大量图片,在逐个批次训练的同时,EM参数的迭代初值u(0)理应得到不断优化。本文中,迭代初值u(0)的维护参考BN中running_mean和running_std的滑动平均更新方式,即:

其中,α∈[0,1]表示动量;u¯(T)表示u(T)在一个mini-batch上的平均。
EMA的迭代过程可以展开为一个RNN,其反向传播也会面临梯度爆炸或消失等问题。此外,公式(8)也要求u(0)和u¯(T)的差异不宜过大,不然初值u(0)的更新也会出现不稳定。RNN中采取LayerNorm(LN)来进行归一化是一个合理的选择。但在EMA中,LN会改变基的方向,进而影响其语义。因为,本文选择L2Norm来对基进行归一化。这样,u(0)的更新轨迹便处在一个高维球面上。
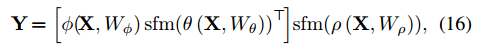
A2 Net中提出的Double Attention Block可以看作EMAU的特殊例子,它只迭代一次EM,且u由反向传播来更新。而EMAU迭代T步,用滑动平均来更新u。其中sfm表示softmax函数。
实验结果:
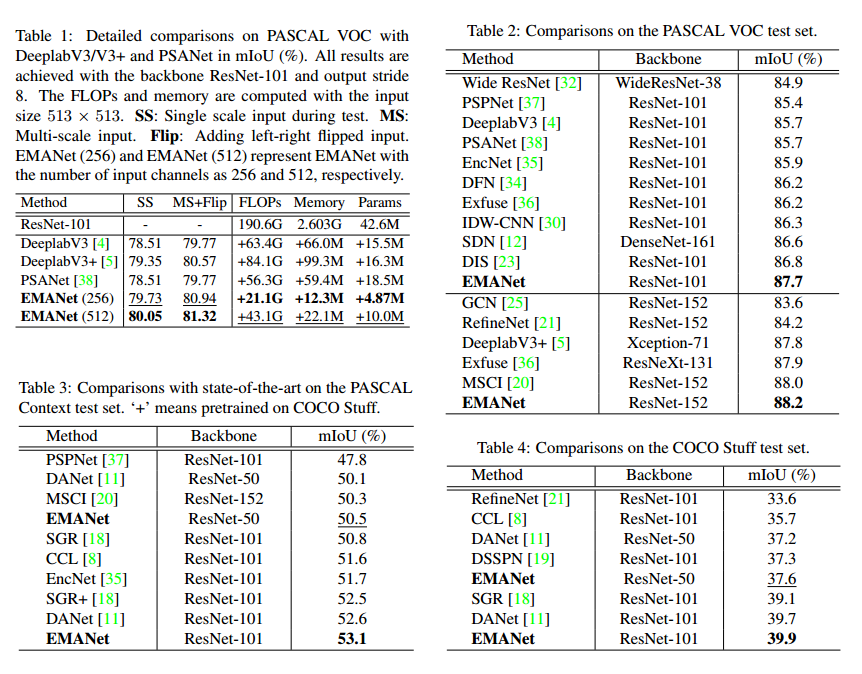
EMANet具有参数量少,精度高的优点。

通过注意力可视化图,i,j,k,l表示四个随机选择的基的下标,右边四列绘出的是它们各自对应的注意力图。可以看到,不同的基会收敛到一些特定的语义概念。
总结:
论文首次基于期望最大化的思路提出期望最大化注意力模块expectation-maximization attention (EMA),同时将该模块实现为神经网络单元,实现了真正的即插即用,方便移植进任何网络结构。同时EMANet具有精度高,参数量少的优点。
参考:
https://zhuanlan.zhihu.com/p/78018142