一、题目描述
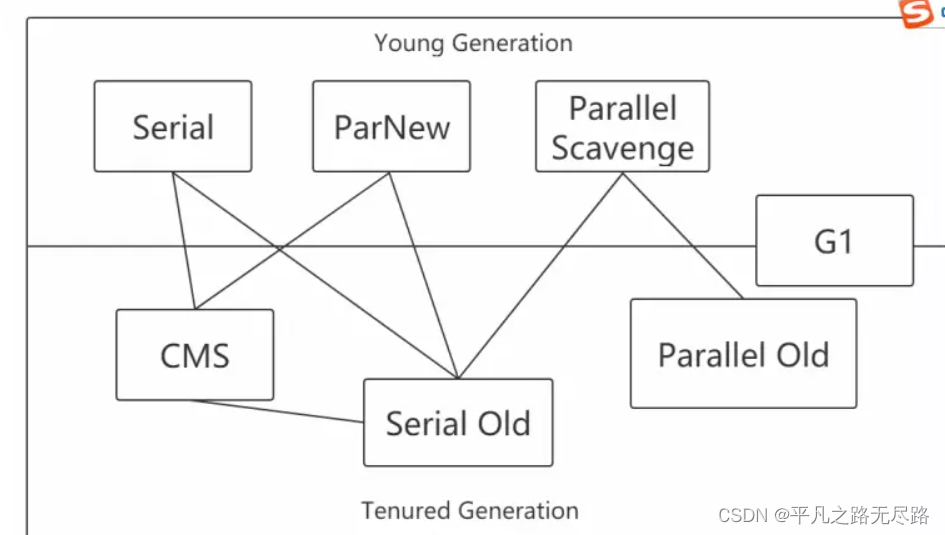
众所周知红黑树是一种平衡树,它最突出的特性就是不能有两个相邻的红色节点。
那我们定义一个红黑图,也就是一张无向图中,每个节点可能有红黑两种颜色,但我们必须保证没有两个相邻的红色节点。
现在给出一张未染色的图,只能染红黑两色,问总共有多少种染色方案使得它成为一个红黑图。
二、输入描述
第一行两个数字n m,表示图中有n个节点和m条边。
接下来共计m行,每行两个数字s t,表示一条连接节点s和节点t的边,节点编号为[0,n)。
三、输出描述
一个数字表示总的染色方案数。
四、补充说明
0<n<15
0<=m <=n * 30<= s, t < n不保证图连通
保证没有重边和自环
五、解题思路
- 读取输入的节点数n和边数m。
- 创建一个空的列表list,用于存储边的信息。
- 循环m次,读取每条边的起始节点和结束节点,将其存储为一个长度为2的数组,然后添加到列表list中。
- 计算红黑图的可能性总数。假设有n个节点,那么总的可能性数为2的n次方。
- 初始化变量num为总的可能性数n。
- 遍历从0到n的所有可能性:
- 对于每个可能性,遍历列表list中的每条边。
- 使用位运算判断起始节点和结束节点是否都被染色(对应位为1)。
- 如果起始节点和结束节点都被染色,表示出现了两个相邻的红色节点,将num减1,并结束当前遍历。
- 输出num作为结果。
六、Python算法源码
def calculate_coloring_options(n, edges):
num = 2 ** n
count = num
for i in range(num):
for j in range(len(edges)):
start, end = edges[j]
start_mask = 1 << start
end_mask = 1 << end
if (start_mask & i) != 0 and (end_mask & i) != 0:
count -= 1
break
return count
七、效果展示
1、输入
3 3
0 1
0 2
1 2
2、输出
4

🏆下一篇:华为OD机试真题 Python 实现【相对开音节】【2022Q4 100分】,附详细解题思路
🏆本文收录于,华为OD机试(Python)真题(A卷+B卷)
每一题都有详细的答题思路、详细的代码注释、样例测试,订阅后,专栏内的文章都可看,可加入华为OD刷题群(私信即可),发现新题目,随时更新,全天CSDN在线答疑。