2022 年全国硕士研究生入学统一考试管理类专业学位联考数学试题
一、问题求解:第 1∼15 小题,每小题 3 分,共 45 分。下列每题给出的 A、B、C、D、E 五个选项中,只有一项是符合试题要求的,请在答.题.卡.上将所选项的字母涂黑。
1.一项工程施工 3 天后,因故障停工 2 天,之后工程队提高工作效率 20%,仍能按原计划完成,则原计划工期为( ).
A.9 天
B.10 天
C.12 天
D.15 天
E.18 天
2.某商品的成本利润率为 12%,若其成本降低 20%,而售价不变,则利润率为( ).
A. 32%
B. 35%
C. 40%
D. 45%
E. 48%
3.设𝑥,𝑦为实数,则
f
(
x
,
y
)
=
x
2
+
4
x
y
+
5
y
2
−
2
y
+
2
f(x,y)=x^2+4xy+5y^2-2y+2
f(x,y)=x2+4xy+5y2−2y+2,则最小值为( ).
A.1
B.
1
2
\frac{1}{2}
21
C.2
D.
3
2
\frac{3}{2}
23
E.3
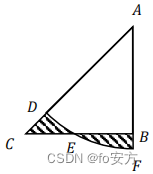
4.如图,△𝐴𝐵𝐶一个等腰直角三角形,以 A 为圆心的圆弧交 AC 于 D,交 BC 于 E,交 AB的延长线于 F,若曲边三角形 CDE 与BEF 的面积相等,则
A
D
A
C
\frac{AD}{AC}
ACAD =( ).
A.
3
2
\frac{\sqrt{3}}{2}
23
B.
2
5
\frac{2}{\sqrt{5}}
52
C.
3
π
\sqrt\frac{{3}}{π}
π3
D.
π
2
\frac{\sqrt{π}}{2}
2π
E.
2
π
\sqrt\frac{{2}}{π}
π2
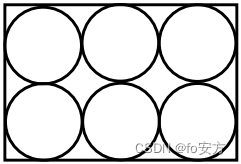
5.如图,已知相邻的圆都相切,从这 6 个圆中随机取 2 个,这 2 个圆不相切的概率为
( )
A.
8
15
\frac{8}{15}
158
B.
7
15
\frac{7}{15}
157
C.
3
5
\frac{3}{5}
53
D.
2
5
\frac{2}{5}
52
E.
2
3
\frac{2}{3}
32
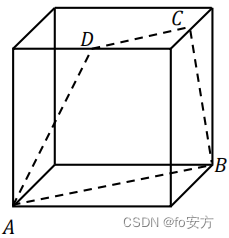
6.如图,在棱长为 2 的正方体中,𝐴,𝐵是顶点,𝐶,𝐷是所在棱的中点,则四边形𝐴𝐵𝐶𝐷的面积为( )
A.
9
2
\frac{9}{2}
29
B.
7
2
\frac{7}{2}
27
C.
3
2
2
\frac{3{\sqrt{2}}}{2}
232
D.
2
5
2{\sqrt{5}}
25
E.
3
2
3{\sqrt{2}}
32
7.桌上放有 8 只杯子,将其中的 3 只杯子翻转(杯口朝上与朝下互换)作为一次操作,8 只杯口朝上的杯子经𝑛𝑛次操作后,杯口全部朝下,则𝑛𝑛的最小值为( ).
A.3
B.4
C.5
D.6
E.8
8.某公司有甲、乙、丙三个部门,若从甲部门调 26 人去丙部门,则丙部门是甲部门人数的6 倍;若从乙部门调 5 人去丙部门,则丙部门的人数与乙部门人数相等.则甲、乙两部门人数之差除以 5 的余数是( ).
A.0
B.1
C.2
D.3
E.4
9.直角△ 𝐴𝐵𝐶中, 𝐷为斜边𝐴𝐶的中点,以𝐴𝐷为直径的圆交𝐴𝐵于𝐸,则△ 𝐴𝐵𝐶的面积为8, 则△ 𝐴𝐸𝐷的面积为( ).
A.1
B.2
C.3
D.4
E.6
10.一个自然数的各位数字都是 105 的质因数,且每个质因数最多出现一次,这样的自然数有( )个.
A.6
B.9
C.12
D.15
E.27
11.购买 A 玩具和 B 玩具各 1 件,需花费 1.4 元,购买 200 件 A 玩具和 150 件 B 玩具需花费 250 元,则 A 玩具的单价为( ).
A.0.5 元
B.0.6 元
C. 0.7 元
D. 0.8 元
E. 0.9 元
12.甲乙两支足球队进行比赛,比分为 4:2,且在比赛过程中乙队没有领先过,则不同的进球顺序有( ).
A.6 种
B. 8 种
C. 9 种
D. 10 种
E. 12 种
13.4 名男生和 2 名女生随机站成一排,则女生既不在两端也不相邻的概率为( )
A.
1
2
\frac{1}{2}
21
B.
5
12
\frac{5}{12}
125
C.
3
8
\frac{3}{8}
83
D.
1
3
\frac{1}{3}
31
E.
1
5
\frac{1}{5}
51
14.已知 AB 两地相距 208km,甲、乙、丙三车的速度分别为 60km/h,80km/h,90km/h 甲乙两车从 A 地出发去 B 地,丙车从 B 地出发去A 地,三车同时出发,当丙车与甲、乙两车距离相等时,用时( )
A.70
B.75
C.78
D.80
E.86
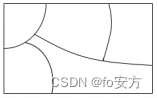
15.如图,用 4 种颜色对图中五块区域进行涂色,每块区域涂一种颜色,且相邻的两块区域颜色不同,不同的涂色方法有( )种
A.12
B.24
C.32
D.48
E.96
二、条件充分性判断:第 16∼25 小题,每小题 3 分,共 30 分.要求判断每题给出的条件(1)和条件(2)能否充分支持题干所陈述的结论.A、B、C、D、E 五个选项为判断结果,请选择一项符合试题要求的判断.
A:条件(1)充分,但条件(2)不充分.
B:条件(2)充分,但条件(1)不充分.
C:条件(1)和(2)单独都不充分,但条件(1)和条件(2)联合起来充分.
D:条件(1)充分,条件(2)也充分.
E:条件(1)和(2)单独都不充分,条件(1)和条件(2)联合起来也不充分.
16.如图,𝐴𝐷与圆相切于点𝐷,𝐴𝐶与圆相交于𝐵𝐶,则能确定△ 𝐴𝐵𝐷与△ 𝐵𝐷𝐶的面积之比.
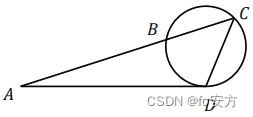
(1)已知
A
D
C
D
\frac{AD}{CD}
CDAD
(2)已知
B
D
C
D
\frac{BD}{CD}
CDBD
17.设实数𝑥𝑥满足|𝑥 − 2| − |𝑥 − 3| = 𝑎,则能确定𝑥的值.
(1)0 < 𝑎 ≤
1
2
\frac{1}{2}
21
(2)
1
2
\frac{1}{2}
21 < 𝑎 ≤ 1.
18.两个人数不等的班数学测验的平均分不相等,则能确定人数多的班
(1)己知两个班的平均成绩.
(2)己知两个班的总平均值.
19.在△ 𝐴𝐵𝐶 中,𝐷 为 𝐵𝐶 边上的点, 𝐵𝐷 、 𝐴𝐵 、 𝐵𝐶 成等比数列,则 ∠𝐵𝐴𝐶 = 90°
(1)𝐵𝐷 = 𝐷𝐶 .
(2) 𝐴𝐷 ⊥ 𝐵𝐶.
20.将 75 名学生分成 25 组,每组 3 人,则能确定女生人数.
(1)已知全是男生的组数和全是女生的组数.
(2)只有 1 男的组和只有 1 女的组数相等.
21.某直角三角形的三边长 𝑎 , 𝑏 , 𝑐 成等比数列,则能确定公比的值
(1)𝑎 是直角边长
(2)𝑐 是斜边长
22.已知𝑥𝑥为正实数,则能确定𝑥−
1
x
\frac{1}{x}
x1的值
(1)已知
x
+
1
x
{\sqrt{x}}+\frac{1}{\sqrt{x}}
x+x1的值
(2)已知
x
2
−
1
x
2
x^2-\frac{1}{x^2}
x2−x21的值
23.已知𝑎,𝑏为实数,则能确定𝑎的值.
(1)𝑎,𝑏,𝑎 + 𝑏成等比数列
(2)𝑎(𝑎 + 𝑏) > 0
24.已知正数列{
a
n
a_n
an},则{
a
n
a_n
an}是等差数列
(1)
a
n
+
1
2
−
a
n
2
=
2
n
,
n
=
1
,
2
,
.
.
.
a_{n+1}^2-a_n^2=2n,n=1,2,...
an+12−an2=2n,n=1,2,...
(2)
a
1
+
a
3
=
2
a
2
a_1+a_3=2a_2
a1+a3=2a2
- 设实数𝑎,𝑏满足|𝑎 − 2𝑏| ≤ 1,则|𝑎| > |𝑏|
(1)|𝑏| > 1
(2)|𝑏| < 1
参考答案
1-5 DCAEA
6-10 ABCBD
11-15 DCECE
16-20 BACBC
21-25 DBECA