目录

题目描述

输入描述

输出描述

用例

题目解析

算法源码

---

题目描述

给定坐标轴上的一组线段，线段的起点和终点均为整数并且长度不小于1，请你从中找到最少数量的线段，这些线段可以覆盖柱所有线段。

输入描述

第一行输入为所有线段的数量，不超过10000，后面每行表示一条线段，格式为"x,y"，x和y分别表示起点和终点，取值范围是[-10^5，10^5]。

输出描述

最少线段数量，为正整数

用例

输入	3 1,4 2,5 3,6
输出	2
说明	无

题目解析

用例1图示如下

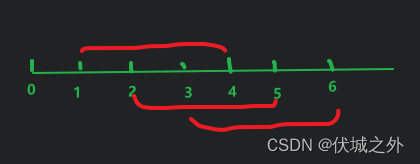
可以发现，只要选择[]1,4[和[3,6]就可以覆盖住所有给定线段。

我的解题思路如下：

首先，将所有区间ranges按照开始位置升序，如果开始位置相同，则按照结束位置降序。

然后，创建一个辅助的栈stack，初始时将排序后的第一个区间压入栈中。

然后，遍历出1~ranges.length范围内的每一个区间ranges[i]，将遍历到ranges[i]和stack栈顶区间对比：

• 如果stack栈顶区间可以包含ranges[i]区间，则range[i]不压入栈顶
• 如果stack栈顶区间被ranges[i]区间包含，则弹出stack栈顶元素，继续比较ranges[i]和stack新的栈顶元素
• 如果stack栈顶区间和ranges[i]无法互相包含，只有部分交集，则将ranges[i]区间去除交集部分后，剩余部分区间压入stack
• 如果stack栈顶区间和ranges[i]区间没有交集，那么直接将ranges[i]压入栈顶

这样的话，最终stack中有多少个区间，就代表至少需要多少个区间才能覆盖所有线段。

比如，用例1的运行流程如下：

 

 

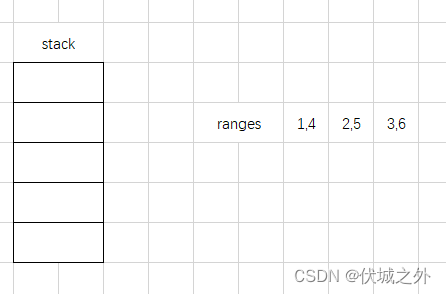
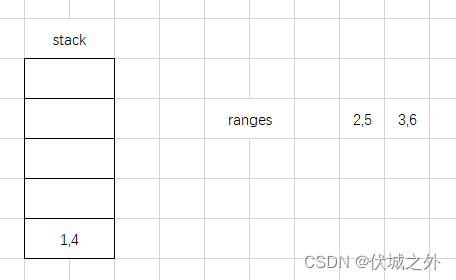
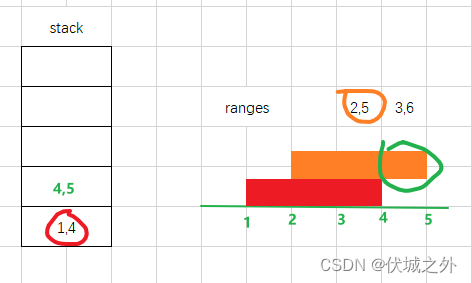
2,5 和 1,4 存在重叠区间，我们只保留2,5区间的非重叠部分4,5

 

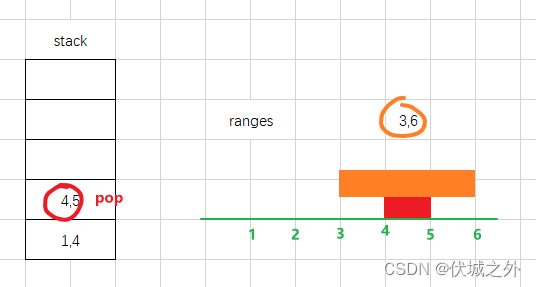
比较4,5区间和3,6区间，发现3,6完全涵盖2,5,因此2,5区间不再需要，可以从stack中弹栈删掉，即原始的2,5区间被删除了。

 

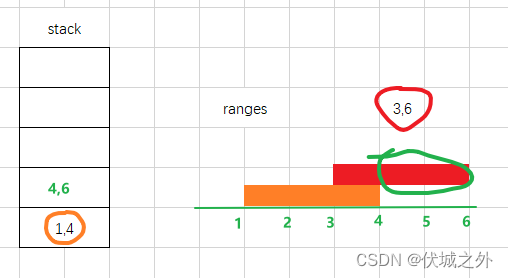
继续比较1,4和3,6区间，发现无法互相涵盖，因此都需要保留，但是3,6有部分区间和1,4重叠，因此只保留3,6不重叠部分4,6。

最终只需要两个区间，对应1,4、3,6，即可涵盖所有线段 

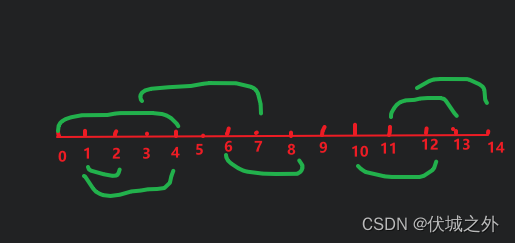
自测用例：

8
0,4
1,2
1,4
3,7
6,8
10,12
11,13
12,14

 输出5，即至少需要上面标红的五个区间才能覆盖所有线段。

算法源码

/* JavaScript Node ACM模式 控制台输入获取 */
const readline = require("readline");

const rl = readline.createInterface({
  input: process.stdin,
  output: process.stdout,
});

const lines = [];
let n;
rl.on("line", (line) => {
  lines.push(line);

  if (lines.length === 1) {
    n = lines[0] - 0;
  }

  if (n && lines.length === n + 1) {
    lines.shift();
    const ranges = lines.map((line) => line.split(",").map(Number));
    console.log(getResult(ranges, n));

    lines.length = 0;
  }
});

function getResult(ranges, n) {
  ranges.sort((a, b) => (a[0] === b[0] ? b[1] - a[1] : a[0] - b[0]));

  const stack = [ranges[0]];

  for (let i = 1; i < ranges.length; i++) {
    const [s2, e2] = ranges[i];

    while (true) {
      const [s1, e1] = stack.at(-1);

      if (s2 <= s1) {
        if (e2 >= e1) stack.pop();
      } else if (s2 < e1) {
        if (e2 > e1) {
          stack.push([e1, e2]);
        }
        break;
      } else {
        stack.push(ranges[i]);
        break;
      }
    }
  }
  console.log(stack);
  return stack.length;
}