岭回归

数据的特征比样本点还多，非满秩矩阵在求逆时会出现问题

岭回归即我们所说的L2正则线性回归，在一般的线性回归最小化均方误差的基础上增加了一个参数w的L2范数的罚项，从而最小化罚项残差平方和

简单说来，岭回归就是在普通线性回归的基础上引入单位矩阵。回归系数的计算公式变形如下

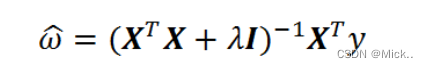
 岭回归最先用来处理特征数多于样本数的情况，现在也用于在估计中加入偏差，从而得到更好的估计。这里通过引入λ来限制了所有w之和，通过引入该惩罚项，能够减少不重要的参数，这个技术在统计学中也可以叫做缩减（shrinkage）。

缩减方法可以去掉不重要的参数，因此能更好地裂解数据。此外，与简单的线性回归相比，缩减法能够取得更好的预测效果

为了使用岭回归和缩减技术，首先需要对特征做标准化处理。因为，我们需要使每个维度特征具有相同的重要性。本文使用的标准化处理比较简单，就是将所有特征都减去各自的均值并除以方差。

from matplotlib.font_manager import FontProperties
import matplotlib.pyplot as plt
import numpy as np
def loadDataSet(fileName):
    """
    函数说明:加载数据
    Parameters:
        fileName - 文件名
    Returns:
        xArr - x数据集
        yArr - y数据集
    """
    numFeat = len(open(fileName).readline().split('\t')) - 1
    xArr = []; yArr = []
    fr = open(fileName)
    for line in fr.readlines():
        lineArr =[]
        curLine = line.strip().split('\t')
        for i in range(numFeat):
            lineArr.append(float(curLine[i]))
        xArr.append(lineArr)
        yArr.append(float(curLine[-1]))
    return xArr, yArr
def ridgeRegres(xMat, yMat, lam = 0.2):
    """
    函数说明:岭回归
    Parameters:
        xMat - x数据集
        yMat - y数据集
        lam - 缩减系数
    Returns:
        ws - 回归系数
    """
    xTx = xMat.T * xMat
    denom = xTx + np.eye(np.shape(xMat)[1]) * lam
    if np.linalg.det(denom) == 0.0:
        print("矩阵为奇异矩阵,不能转置")
        return
    ws = denom.I * (xMat.T * yMat)
    return ws
def ridgeTest(xArr, yArr):
    """
    函数说明:岭回归测试
    Parameters:
        xMat - x数据集
        yMat - y数据集
    Returns:
        wMat - 回归系数矩阵
    """
    xMat = np.mat(xArr);
    yMat = np.mat(yArr).T
    #数据标准化
    yMean = np.mean(yMat, axis = 0)                        #行与行操作，求均值
    yMat = yMat - yMean                                    #数据减去均值
    xMeans = np.mean(xMat, axis = 0)                    #行与行操作，求均值
    xVar = np.var(xMat, axis = 0)                        #行与行操作，求方差
    xMat = (xMat - xMeans) / xVar                        #数据减去均值除以方差实现标准化
    numTestPts = 20                                  #30个不同的lambda测试
    wMat = np.zeros((numTestPts, np.shape(xMat)[1]))    #初始回归系数矩阵
    for i in range(numTestPts):                            #改变lambda计算回归系数
        ws = ridgeRegres(xMat, yMat, np.exp(i - 10))    #lambda以e的指数变化，最初是一个非常小的数，
        wMat[i, :] = ws.T                                 #计算回归系数矩阵
    return wMat
def plotwMat():
    """
    函数说明:绘制岭回归系数矩阵
    """
    font = FontProperties(fname=r"c:\windows\fonts\simsun.ttc", size=14)
    abX, abY = loadDataSet('abalone.txt')
    redgeWeights = ridgeTest(abX, abY)
    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.plot(redgeWeights)
    ax_title_text = ax.set_title(u'log(lambada)与回归系数的关系', FontProperties = font)
    ax_xlabel_text = ax.set_xlabel(u'log(lambada)', FontProperties = font)
    ax_ylabel_text = ax.set_ylabel(u'回归系数', FontProperties = font)
    plt.setp(ax_title_text, size = 20, weight = 'bold', color = 'red')
    plt.setp(ax_xlabel_text, size = 10, weight = 'bold', color = 'black')
    plt.setp(ax_ylabel_text, size = 10, weight = 'bold', color = 'black')
    plt.show()
if __name__ == '__main__':
    plotwMat()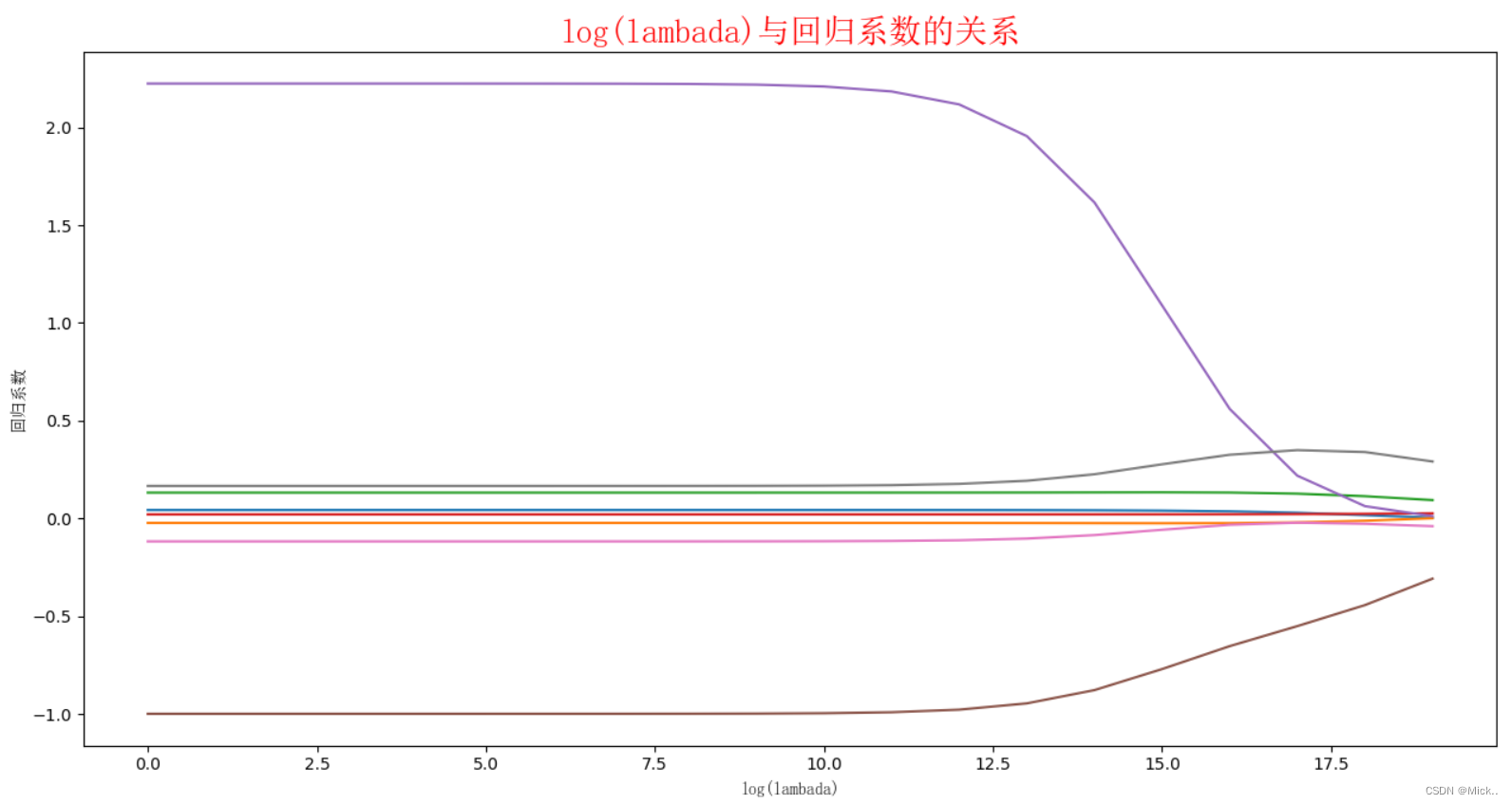

前向逐步线性回归

前向逐步线性回归算法属于一种贪心算法，即每一步都尽可能减少误差。我们计算回归系数，不再是通过公式计算，而是通过每次微调各个回归系数，然后计算预测误差。那个使误差最小的一组回归系数，就是我们需要的最佳回归系数

from matplotlib.font_manager import FontProperties
import matplotlib.pyplot as plt
import numpy as np


def loadDataSet(fileName):
    """
    函数说明:加载数据
    Parameters:
        fileName - 文件名
    Returns:
        xArr - x数据集
        yArr - y数据集
    """
    numFeat = len(open(fileName).readline().split('\t')) - 1
    xArr = [];
    yArr = []
    fr = open(fileName)
    for line in fr.readlines():
        lineArr = []
        curLine = line.strip().split('\t')
        for i in range(numFeat):
            lineArr.append(float(curLine[i]))
        xArr.append(lineArr)
        yArr.append(float(curLine[-1]))
    return xArr, yArr


def regularize(xMat, yMat):
    """
    函数说明:数据标准化
    Parameters:
        xMat - x数据集
        yMat - y数据集
    Returns:
        inxMat - 标准化后的x数据集
        inyMat - 标准化后的y数据集
    """
    inxMat = xMat.copy()  # 数据拷贝
    inyMat = yMat.copy()
    yMean = np.mean(yMat, 0)  # 行与行操作，求均值
    inyMat = yMat - yMean  # 数据减去均值
    inMeans = np.mean(inxMat, 0)  # 行与行操作，求均值
    inVar = np.var(inxMat, 0)  # 行与行操作，求方差
    inxMat = (inxMat - inMeans) / inVar  # 数据减去均值除以方差实现标准化
    return inxMat, inyMat


def rssError(yArr, yHatArr):
    """
    函数说明:计算平方误差
    Parameters:
        yArr - 预测值
        yHatArr - 真实值
    Returns:
    """
    return ((yArr - yHatArr) ** 2).sum()


def stageWise(xArr, yArr, eps=0.01, numIt=100):
    """
    函数说明:前向逐步线性回归
    Parameters:
        xArr - x输入数据
        yArr - y预测数据
        eps - 每次迭代需要调整的步长
        numIt - 迭代次数
    Returns:
        returnMat - numIt次迭代的回归系数矩阵
    """
    xMat = np.mat(xArr)
    yMat = np.mat(yArr).T  # 数据集
    xMat, yMat = regularize(xMat, yMat)  # 数据标准化
    m, n = np.shape(xMat)
    returnMat = np.zeros((numIt, n))  # 初始化numIt次迭代的回归系数矩阵
    ws = np.zeros((n, 1))  # 初始化回归系数矩阵
    wsTest = ws.copy()
    wsMax = ws.copy()
    for i in range(numIt):  # 迭代numIt次
        # print(ws.T)                                                                    #打印当前回归系数矩阵
        lowestError = float('inf');  # 正无穷
        for j in range(n):  # 遍历每个特征的回归系数
            for sign in [-1, 1]:
                wsTest = ws.copy()
                wsTest[j] += eps * sign  # 微调回归系数
                yTest = xMat * wsTest  # 计算预测值
                rssE = rssError(yMat.A, yTest.A)  # 计算平方误差
                if rssE < lowestError:  # 如果误差更小，则更新当前的最佳回归系数
                    lowestError = rssE
                    wsMax = wsTest
        ws = wsMax.copy()
        returnMat[i, :] = ws.T  # 记录numIt次迭代的回归系数矩阵
    return returnMat


def plotstageWiseMat():
    """
    函数说明:绘制岭回归系数矩阵
    """
    font = FontProperties(fname=r"c:\windows\fonts\simsun.ttc", size=14)
    xArr, yArr = loadDataSet('abalone.txt')
    returnMat = stageWise(xArr, yArr, 0.005, 1000)
    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.plot(returnMat)
    ax_title_text = ax.set_title(u'前向逐步回归:迭代次数与回归系数的关系', FontProperties=font)
    ax_xlabel_text = ax.set_xlabel(u'迭代次数', FontProperties=font)
    ax_ylabel_text = ax.set_ylabel(u'回归系数', FontProperties=font)
    plt.setp(ax_title_text, size=15, weight='bold', color='red')
    plt.setp(ax_xlabel_text, size=10, weight='bold', color='black')
    plt.setp(ax_ylabel_text, size=10, weight='bold', color='black')
    plt.show()


if __name__ == '__main__':
    plotstageWiseMat()

总结一下：

缩减方法（逐步线性回归或岭回归），就是将一些系数缩减成很小的值或者直接缩减为0。这样做，就增大了模型的偏差（减少了一些特征的权重），通过把一些特征的回归系数缩减到0，同时也就减少了模型的复杂度。消除了多余的特征之后，模型更容易理解，同时也降低了预测误差。但是当缩减过于严厉的时候，就会出现过拟合的现象，即用训练集预测结果很好，用测试集预测就糟糕很多

sklearn.linear_model.Ridge(alpha = .5)

岭回归是一种正则化方法，通过在损失函数中加入L2范数惩罚系项，来控制线性模型的复杂程度，从而使模型更加稳健

class sklearn.linear_model.Ridge(alpha=1.0, fit_intercept=True, normalize=False, copy_X=True, max_iter=None, tol=0.001, solver=’auto’, random_state=None)

参数：

alpha：
       α项，其值越大正则化项越大。其必须是正浮点数。 正则化改善了问题的条件并减少了估计的方差。Alpha对应于其他线性模型（如Logistic回归或LinearSVC）中的C^-1。 如果传递数组，则假定惩罚被特定于目标。 因此，它们必须在数量上对应。
fit_intercept：boolean
       是否计算此模型的截距，即b值。如果为False，则不计算b值（模型会假设你的数据已经中心化）
copy_X：boolean，可选，默认为True
       如果为True，将复制X; 否则，它可能被覆盖。
max_iter：int，可选
       共轭梯度求解器的最大迭代次数。如果为None，则为默认值（不同silver的默认值不同） 对于'sparse_cg'和'lsqr'求解器，默认值由scipy.sparse.linalg确定。 对于'sag'求解器，默认值为1000。
normalize：boolean，可选，默认为False
       如果为真，则回归X将在回归之前被归一化。 当fit_intercept设置为False时，将忽略此参数。 当回归量归一化时，注意到这使得超参数学习更加鲁棒，并且几乎不依赖于样本的数量。 相同的属性对标准化数据无效。 然而，如果你想标准化，请在调用normalize = False训练估计器之前，使用preprocessing.StandardScaler处理数据。
solver：{'auto'，'svd'，'cholesky'，'lsqr'，'sparse_cg'，'sag'}
       指定求解最优化问题的算法：
'auto'：根据数据类型自动选择求解器。
'svd'：使用X的奇异值分解来计算Ridge系数。对于奇异矩阵比'cholesky'更稳定。
'cholesky'：使用标准的scipy.linalg.solve函数来获得闭合形式的解。
'sparse_cg'：使用在scipy.sparse.linalg.cg中找到的共轭梯度求解器。作为迭代算法，这个求解器比大规模数据（设置tol和max_iter的可能性）的“cholesky”更合适。
'lsqr'：使用专用的正则化最小二乘常数scipy.sparse.linalg.lsqr。它是最快的，但可能不是在旧的scipy版本可用。它还使用迭代过程。
'sag'：使用随机平均梯度下降。它也使用迭代过程，并且当n_samples和n_feature都很大时，通常比其他求解器更快。注意，“sag”快速收敛仅在具有近似相同尺度的特征上被保证。您可以使用sklearn.preprocessing的缩放器预处理数据。
       所有最后四个求解器支持密集和稀疏数据。但是，当fit_intercept为True时，只有'sag'支持稀疏输入。
       新版本0.17支持：随机平均梯度下降解算器。
tol：float
    解的精度，制定判断迭代收敛与否的阈值。
random_state：int seed，RandomState实例或None（默认）
       仅用于'sag'求解器。
如果为整数，则它指定了随机数生成器的种子。
如果为RandomState实例，则指定了随机数生成器。
如果为None，则使用默认的随机数生成器。

属性
coef_：权重向量。
intercept_：float | array，shape =（n_targets，）
       决策函数的独立项，即截距b值。 如果fit_intercept = False，则设置为0.0。
n_iter_：array或None，shape（n_targets，）
       每个目标的实际迭代次数。 仅适用于sag和lsqr求解器。
方法
fit（X，y [，sample_weight]）：训练模型。
get_params（[deep]）：获取此估计器的参数。
predict（X）：使用线性模型进行预测，返回预测值。
score（X，y [，sample_weight]）：返回预测性能的得分，不大于1，越大效果越好。
set_params（** params）设置此估计器的参数

# -*- coding: utf-8 -*-
from sklearn.linear_model import Ridge
import numpy as np
n_samples,n_features=10,5
np.random.seed(0) # seed( ) 用于指定随机数生成时所用算法开始的整数值
y=np.random.randn(n_samples) # randn函数返回一个或一组样本，具有标准正态分布。
X=np.random.randn(n_samples,n_features)
clf=Ridge(alpha=1.0)
#Ridge(alpha=1.0, copy_X=True, fit_intercept=True, max_iter=None,normalize=False, random_state=None, solver='auto', tol=0.001
clf.fit(X,y)
pre=clf.predict(X)
print('真实值 y.shape',y.shape)
print('数据x.shape',X.shape)
print('权重系数',clf.coef_,'coef.shape',clf.coef_.shape)
print('决策函数的独立项',clf.intercept_)
print('预测值',pre)
print('真实值',y)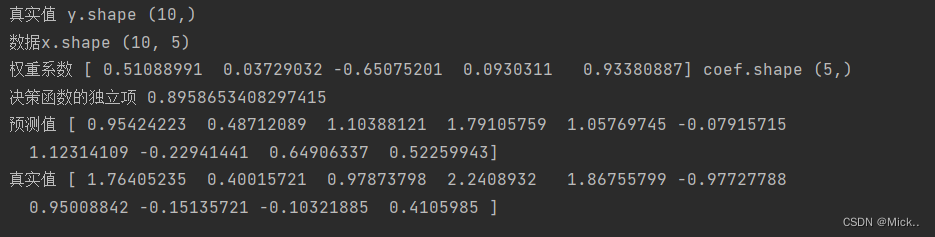

参考文献

机器学习实战教程（十二）：线性回归提高篇之乐高玩具套件二手价预测 (cuijiahua.com)