1> 整理grep、find、cut、tar、apt-get、dpkg、In、In-s指令
a> grep ----->查找字符串
grep 字符串 文件名
-w:按单词查找
-R:实现递归查找,主要用于路径是目录的情况
-i:不区分大小写
-n:显示行号
例:
grep -w "^ubuntu" /etc/passwd ---->查找以ubuntu单词作为开头位置的所在行
grep -w "ubuntu$" /etc/passwd ---->查找以Ubuntu为结尾的所在行
grep -w "^ubuntu$" /etc/passwd --->查找开头和结尾都是Ubuntu的所在行,(这一行只能有ubuntu)
b> find ----->查找文件
find 查找的路径 -name 文件名 ----->在指定路径下,以文件名为条件查找文件
find -name 文件名 ----->在当前路径下,查找文件
find -name *.c ---->find可以进行模糊查找,不建议使用
c> cut ----->截取字符串
cut -d "分隔符" -f "域" 文件名
分隔符:要截取的内容以什么作为分隔
域:截分隔后的哪一块
-f后面可以跟的格式 例:"3","3,4","3-5"
d> tar ----->归档/打包和拆包
打包:就是把多个文件合并成一个文件
tar -cvf 打包后的文件名.tar 打包的文件
-v:显示指令执行的过程
-c:实现打包功能的
-f:file -f参数后面一定要跟文件名
压缩:
tar -cvjf 文件名.tar.bz2 要归档压缩的文件
tar -cvJf 文件名.tar.xz 要归档压缩的文件
tar -cvzf 文件名.tar.gz 要归档压缩的文件
压缩工具的参数和文件的后缀,必须严格对应,如果不对应,不会报错,但是生成的不是压缩包
拆包和解压缩:
tar -xvf 要拆包的文件名 ---->万能的拆包解压缩指令,既能完成拆包,也能解压缩
-x:拆包和解压缩
归档/打包和拆包后,源文件仍然存在
e> apt-get ----->在线安装软件
sudo apt-get update ----->拉取软件列表
只要sources.list修改过就需要重新update
sudo apt-get install 软件名 ----->安装软件
例:
sudo apt-get install 软件名
sudo apt-get install oneko 追鼠标的猫
sudo apt-get install lolcat 渐变色
sudo apt-get install gnome-mines 扫雷
sudo apt-get install cowsay 奶牛说
sudo apt-get install cmatrix 代码雨
sudo apt-get remove 软件名 ----->卸载软件
不完全卸载,不删除配置文件
sudo apt-get remove --purge 软件名 ----->完全卸载
完全卸载,包括配置文件
sudo apt-get download 软件名 ----->下载软件安装包,但是不安装软件
sudo apt-get source 软件名 ----->下载软件源码
sudo apt-get clean ----->清空安装包
清空默认下载位置的安装包,/var/cache/apt/archives
f> dpkg ----->离线安装软件
dpkg ----->debian package
软件包的命名规范
sl ----->软件名
_3.03- ----->主版本号
17build2_ ----->修订版本号
amd64 ----->支持64位架构 i386支持32位架构的
.deb ----->debian软件包的后缀名 rpm是redhat软件包的后缀名
sudo dpkg -i 软件包名 ----->安装软件
要求:执行指令的路径下,一定有软件包
sudo dpkg -r 软件名 ----->不完全卸载
sudo dpkg -P 软件名 ----->完全卸载软件
sudo dpkg -l 软件名 ----->查看软件的安装列表
sudo dpkg -L 软件名 ----->查看软件的安装路径
g> ln ----->创建链接文件
ln 被链接文件的路径 创建的硬链接文件的路径
ln创建硬链接文件
1、硬链接文件和源文件有相同的inode号(ls -i)
#inode号,表示文件存储的扇区,有相同的inode号意味着占用同一片空间,硬链接文件是源文件的别名/保存了一个副本
2、硬链接文件的修改会影响到源文件,源文件的修改也会影响硬链接文件
3、ls显示的文件的描述信息中链接文件的个数,指的是硬链接文件的个数
4、只有硬链接文件个数为0时,文件才被删除
h> ln-s ----->创建软链接文件
ln -s 被链接文件的绝对路径 软链接文件的绝对路径
ln -s /home/ubuntu/23041C/day2/1.c /home/ubuntu/23041C/100.c
给/home/ubuntu/23041C/day2/1.c创建了一个路径为/home/ubuntu/23041C/100.c文件
1、创建软链接文件时,使用绝对路径
2、软链接文件可以理解为快捷方式
3、软链接文件的文件类型是l,他不会增加文件描述中的链接文件个数
4、软链接文件,如果源文件被删除,链接会断开,软链接文件会失效,如果重新创建一个同名的源文件,软链接文件会重新链接,并且链接到新创建的文件
5、软链接文件的修改会影响到源文件,源文件的修改也会影响软链接文件
6、wins下不支持软链接文件,Linux下的压缩包不要放到主机下解压
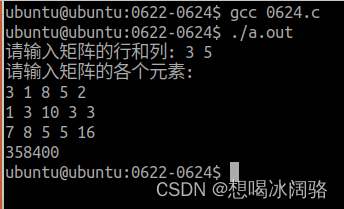
2> 练习:A[n.m]是一个n行m列的矩阵,a[i,j]表示A的第i行j列的元素,定义x[i,j]为A的第i行和第j列除了a[i,j]之外所有元素(共 n+m-2个)的乘积。即x[i,j]=a[i,1]*a[i,2]*…*a[i,j-1]*…*a[i,m]*a[1,j]*al2,j]…*a[i-1,j]+*a[n,j],。现输入非负整形的矩阵A[n,m],求MAX(x[i,j])即所有的x[i,j]中的最大值。 输入描述:第一行两个整数n和m。之后n行输入矩阵、均为非负整数。输出描述:一行输出答案。

#include <myhead.h>
int main(int argc, const char *argv[])
{
//输入矩阵大小
int n=0, m=0;
printf("请输入矩阵的行和列: ");
scanf("%d%d", &n, &m);
//输入矩阵元素
printf("请输入矩阵的各个元素:\n");
int A[n][m];
for(int i=0;i<n;i++)
{
for(int j=0;j<m;j++)
scanf("%d", &A[i][j]);
}
//求最大值
int max = 0;
for(int i=0;i<n;i++)
{
for(int j=0;j<m;j++) //遍历序列
{
int max_temp = 1;
//行乘积
for(int k=0;k<n;k++)
if(k != i)
max_temp *= A[k][j];
//列乘积
for(int k=0;k<m;k++)
if(k != j)
max_temp *= A[i][k];
if(max < max_temp)
max = max_temp;
}
}
printf("%d\n", max);
return 0;
}