串的定义

串的逻辑结构与线性表相似，是一种特殊的线性表，区别仅在于串的数据对象限定为字符；
串通常以整体作为操作的对象，而线性表通常以单个元素作为操作对象。

串或字符串：是由零个或多个字符组成的有序序列
字串：串中任意个连续的字符组成的子序列
空串：零个字符的串
空格串：由空格组成的串

一、串的顺序存储结构

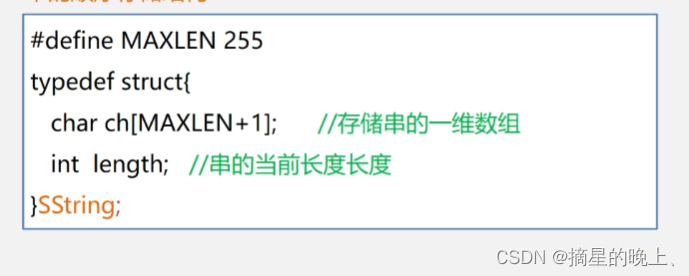
1.1、串的链式存储结构

优点：操作方便
缺点：存储密度低
块链结构可以克服这个缺点

1.2、串的模式匹配算法

字串的定位运算一般称串的模式匹配或串匹配
著名的两种算法：BF 简单匹配法、暴力破解法；KMP （特点：速度快）；
算法应用：搜索引擎、拼写检查、语言翻译、数据压缩；

1.2.1、Brute-Force简称为BF算法

用指针i，j指示主串S和子串T中当前待比较的字符位置，i的初值为pos，j的初值为1
如果两个串均未达到串尾，则循环执行以下操作：
	分别比较指针i，j所指的字符，若相等则指针i，j同时向后移动一位，继续比较
	若字符值不相等，则指针退后重新开始匹配，变成i=i-j+2，j=1，然后重新匹配
	（指针i，j最开始指向下标为1的数组元素，每次回溯时，指针i向后移动一位，指针j回到原点）

模式匹配不一定从主串的第一个位置开始，可以从指定的主串中查找的起始位置开始。

int index_BF(SString S, SString T){
	int i = 1, j = 1;
	while(i<=S.length && j<=T.length){
		if(s.ch[i]==t.cn[j]){++i;++j;} //主串和子串依次匹配下一个字符
		else{i=i-j+2;j=1} //主串、子串指针回溯重新开始下一次匹配 
	}
	if(j>T.length) return i-T.length;  //返回匹配的第一个字符的下标
	else return 0
}

1.2.2、KMP算法

只移动子串，让模式串向右移动，不需要回溯主串指针。
当第一个位置就出现字符不匹配，字串移动到主串的第二位进行比较
当其他位置出现字符不匹配，寻找公共前后缀。
当字符匹配时，子串的比较箭头向后移动一位继续比较。
让模式串向右滑动，将前缀的字符串直接移动到后缀字符串的位置，然后让子串的n号位，再与主串当前位置进行比较。

示例如下图：
定义next[j]函数，表明当前模式中第j个字符与主串中相应字符失配时，在模式中需要重新和主串中该字符进行比较的字符的位置

因为d前面的a b 在主串第一、第二个位置已经匹配到了，所以直接子串移到d前的这两个a b 开始匹配， next[j] = 3 ，从子串的第三个字符开始匹配

int index_KMP(SString S, SString T, int pos){
	i = pos;j=1;
	while(i<S.length&&j<T.length){
		if(j==0||S.ch[i]==T.ch[j]){i++;j++;}
		else(j=next[j]) //i不变 j后退
	}
	if(j>T.length) return i -T.length; //匹配成功
	else return 0;
}

数组的定义

数组是由类型相同的数据元素构成的有序集合，每个元素称为数组元素。(一般用顺序结构)
数组可以看成线性表的推广，其特点是结构中的元素本身可以具有某种结构的数据，但属于同一数据类型。

2.1、数组的顺序存储结构

对于数组，一旦规定了其维度和各维的长度，只要给出一组下标则可以求相应的数组元素的存储位置。
二维数组

设有一个二维数组A[M][N]按行优先顺序存储，假设A[0][0]放在位置644中，A[2][2]放在位置676，每个元素占一个空间，问A[3][3]存放在什么位置
​
2n+2=676-644
n=15
A[3][3]一共有3n+3=48
所以A[3][3]存放在48+644=692的位置上
下标存放从1开始

2.2、数组的特点：结构固定-----维数和维界不变

数组的基本操作：初始化、销毁，取元素、修改元素（一般不做插入和删除操作）

// m行n列，元素总个数mn
typedef elemtype array1[m][n];

// 数组嵌套：一维数组的一维数组
typedef elemtype array1[n];			// 该数组作为二维数组的元素
typedef array1 array2[m];		   // 二维数组，由m个一维数组组成

// n维数组——重复嵌套一维数组
typedef elemtype array1[n1];	  // 1维		
typedef array1 	 array2[n2];	  // 2维
typedef array2	 array3[n3];	  // 3维

2.3、特殊矩阵的压缩存储

所谓压缩存储，是指为多个值相同的元只分配一个储存空间，对零元不分配空间

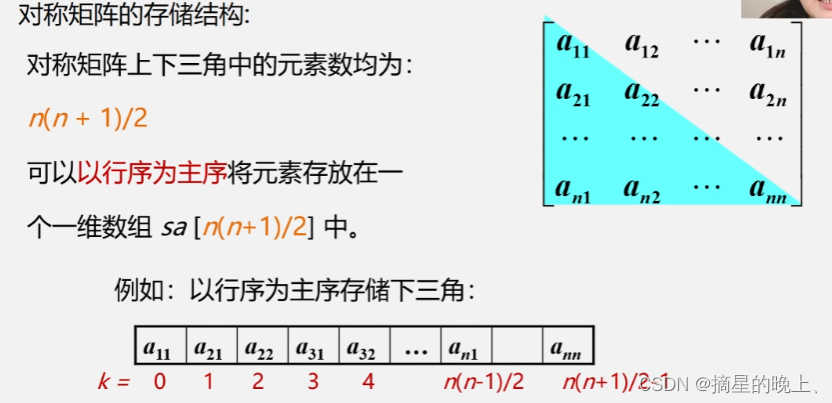
对称矩阵（关于主对角线左右元素相同）
三角矩阵（主对角线一边全为0/常数c）
对角矩阵（所有非零元素都集中在对角线中心的带状区域中，其他元全为0）
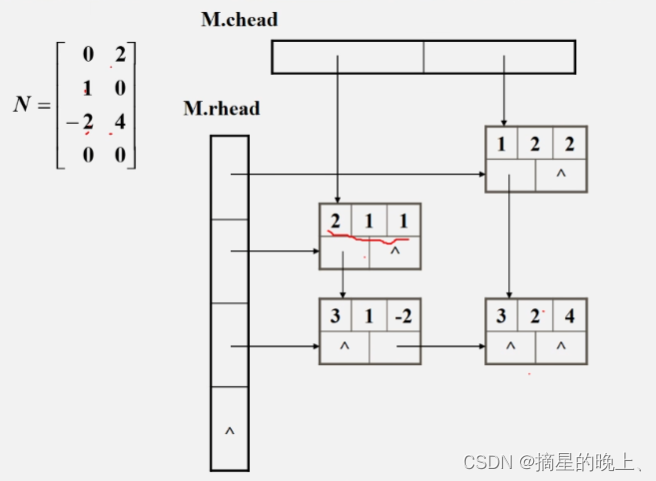
十字链表（链式）
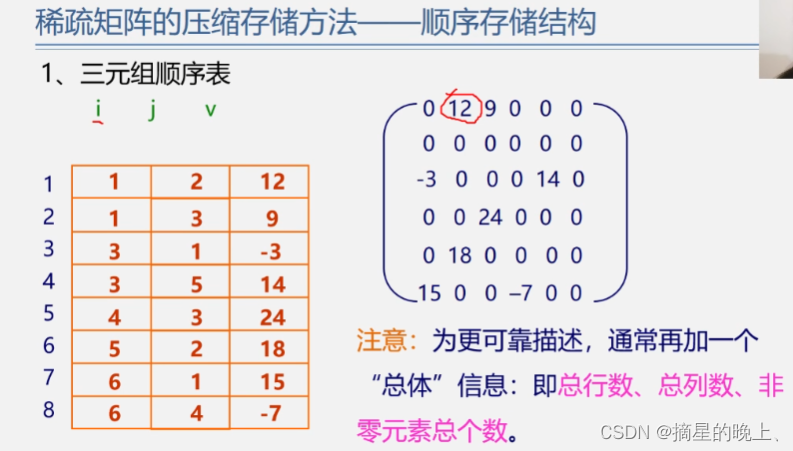
稀疏矩阵（非零个数少）

广义表

3.1、广义表的定义

广义表是线性表的推广，也称为列表。
对于线性表而言，存储的数据元素只能是单个元素，而在广义表中，数据元素可以是单个元素，称为原子，也可以是一个广义表，称为子表。广义表的定义是一个递归的定义。

3.2、广义表的操作

求表头 GetHead(L)

非空广义表的第一个元素，可以试试一个元素也可以是一个子表

求表尾 GetTail(L)

非空广义表除去表头元素意外的其他元素所构成的表，表尾一定是一个表。

3.3、广义表与线性表的区别

广义表可以看成是线性表的推广，线性表是广义表的特例。
广义表的结构相当灵活，在某种前提下，它可以兼容线性表、数组、树和有向图等各种常用的数据结构。
当二维数组的每行(或每列)作为子表处理时，二维数组即为一个广义表。
另外，树和有向图也可以用广义表来表示。
由于广义表不仅集中了线性表、数组、树和有向图等常见数据结构的特点，而且可有效地利用存储空间，因此在计算机的许多应用领域都有成功使用广义表的实例。