目录

第一章 线性表

第二章 栈和队列

第三章 字符串

第四章 广义表

第五章 树

第六章 图

第七章 查找

第八章 内排序

---

第一章 线性表

• 一个线性表是n个数据元素的优先序列
• 线性表可分为顺序存储结构（数组）和链式存储结构（链表）
• 链表可分为单链表、循环链表、双向链表

顺序表 Sequence Table

#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <stdbool.h>

#define CAPACITY 4

typedef int SData;

typedef struct Sequence
{
	SData* data;
	int size;
	int capacity;
}Sequence;

void Init(Sequence* ps)
{
	assert(ps);
	ps->data = (SData*)malloc(sizeof(SData) * CAPACITY);
	ps->size = 0;
	ps->capacity = CAPACITY;
}

void CheckCapacity(Sequence* ps)
{
	if (ps->size == ps->capacity)
	{
		ps->data = realloc(ps->data, sizeof(SData) * ps->size * 2);
		if (ps->data == NULL)
		{
			perror("realloc");
			exit(-1);
		}
		ps->capacity *= 2;
	}
}

bool Empty(Sequence* ps)
{
	assert(ps);
	if (ps->size == 0)
		return true;
	return false;
}

void Push(Sequence* ps, SData x)
{
	assert(ps);
	CheckCapacity(ps);
	ps->data[ps->size] = x;
	++ps->size;
}

void Pop(Sequence* ps)
{
	assert(ps);
	assert(!Empty(ps));
	--ps->size;
}

int Find(Sequence* ps, SData x)
{
	assert(ps);
	int pos = 0;
	for (; pos < ps->size; ++pos)
	{
		if (ps->data[pos] == x)
			return pos;
	}
	return -1;
}

void Insert(Sequence* ps, int pos, SData x)
{
	assert(ps);
	assert(pos <= ps->size);
	CheckCapacity(ps);
	int i = ps->size;
	for (; i >= pos; --i)
	{
		ps->data[i + 1] = ps->data[i];
	}
	ps->data[pos] = x;
	++ps->size;
}

void Erase(Sequence* ps, int pos)
{
	assert(ps);
	assert(!Empty(ps));
	int i = pos;
	for (; i < ps->size - 1; ++i)
	{
		ps->data[i] = ps->data[i + 1];
	}
	--ps->size;
}

void Print(Sequence* ps)
{
	assert(ps);
	int i = 0;
	for (; i < ps->size; ++i)
	{
		printf("%d ", ps->data[i]);
	}
	printf("\n");
}

int main()
{
	Sequence s;
	Init(&s);
	Push(&s, 1);
	Push(&s, 2);
	Push(&s, 3);
	Push(&s, 4);
	Push(&s, 5);
	Print(&s);
	Insert(&s, 0, 10);
	Insert(&s, 3, 20);
	Insert(&s, 7, 30);
	Print(&s);
	Pop(&s);
	Erase(&s, 0);
	Erase(&s, Find(&s, 20));
	Print(&s);
	return 0;
}

带头双向循环链表 Linked List

#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <stdbool.h>

typedef int LData;

typedef struct List
{
	LData data;
	struct List* next;
	struct List* prev;
}List;

void Init(List* pl)
{
	assert(pl);
	pl->next = pl;
	pl->prev = pl;
}

bool Empty(List* pl)
{
	assert(pl);
	if (pl->next == pl)
		return true;
	return false;
}

void Insert(List* pl, List* pos, LData x)
{
	assert(pl);
	List* new_node = (List*)malloc(sizeof(List));
	new_node->data = x;
	new_node->next = pos;
	new_node->prev = pos->prev;
	pos->prev->next = new_node;
	pos->prev = new_node;
}

void Erase(List* pl, List* pos)
{
	assert(pl);
	assert(pos);
	assert(!Empty(pl));
	List* next = pos->next;
	List* prev = pos->prev;
	prev->next = next;
	next->prev = prev;
	free(pos);
	pos = NULL;
}

void Push(List* pl, LData x)
{
	assert(pl);
	if (Empty(pl))
	{
		List* new_node = (List*)malloc(sizeof(List));
		new_node->data = x;
		new_node->prev = pl;
		new_node->next = pl;
		pl->next = new_node;
		pl->prev = new_node;
	}
	else
	{
		Insert(pl, pl, x);
	}
}

void Pop(List* pl)
{
	assert(pl);
	assert(!Empty(pl));
	Erase(pl, pl->prev);
}

List* Find(List* pl, LData x)
{
	assert(pl);
	List* cur = pl->next;
	while (cur != pl)
	{
		if (cur->data == x)
			return cur;
		cur = cur->next;
	}
	return NULL;
}

void Print(List* pl)
{
	assert(pl);
	List* cur = pl->next;
	while (cur != pl)
	{
		printf("%d ", cur->data);
		cur = cur->next;
	}
	printf("\n");
}

int main()
{
	List list;
	Init(&list);
	Push(&list, 1);
	Push(&list, 2);
	Push(&list, 3);
	Push(&list, 4);
	Print(&list);
	Insert(&list, Find(&list, 1), 10);
	Insert(&list, Find(&list, 2), 20);
	Insert(&list, Find(&list, 4), 40);
	Print(&list);
	Pop(&list);
	Erase(&list, Find(&list, 10));
	Erase(&list, Find(&list, 20));
	Print(&list);
	Print(&list);
	return 0;
}

第二章 栈和队列

• 栈：先进后出，一般为顺序存储结构
• 队列：先进先出，一般为链式存储结构

循环队列：

• 顺序存储结构，设置容量(capacity)及头尾下标(front、rear)
• push：++rear，    pop：++front，当下标等于capacity时变为0
• 为区分“满”和“空”，舍弃一个元素空间，使 (rear + 1) % capacity == front 为判“满”

栈 Stack （顺序存储） 检查括号是否匹配

#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <stdbool.h>

#define CAPACITY 4

typedef char SData;

typedef struct Stack
{
	SData* data;
	int size;
	int capacity;
}Stack;

void Init(Stack* s)
{
	assert(s);
	s->data = (SData*)malloc(sizeof(SData) * CAPACITY);
	s->size = 0;
	s->capacity = CAPACITY;
}

bool Empty(Stack* s)
{
	assert(s);
	if (s->size == 0)
		return true;
	return false;
}

void CheckCapacity(Stack* s)
{
	assert(s);
	if (s->size == s->capacity)
	{
		s->data = (SData*)realloc(s->data, sizeof(SData) * s->capacity * 2);
		s->capacity *= 2;
	}
}

void Push(Stack* s, SData x)
{
	assert(s);
	CheckCapacity(s);
	s->data[s->size] = x;
	++s->size;
}

void Pop(Stack* s)
{
	assert(s);
	assert(!Empty(s));
	--s->size;
}

SData Top(Stack* s)
{
	assert(s);
	return s->data[s->size - 1];
}

int Size(Stack* s)
{
	assert(s);
	return s->size;
}

void CheckBrackets(Stack* s, char* str)
{
	assert(s);
	char* cur = str;
	while (*cur != '\0')
	{
		if (*cur == '{' || *cur == '[' || *cur == '(')
		{
			Push(s, *cur);
		}
		else if (*cur == '}' || *cur == ']' || *cur == ')')
		{
			if (*cur == '}' && Top(s) == '{')
			{
				Pop(s);
			}
			else if (*cur == ']' && Top(s) == '[')
			{
				Pop(s);
			}
			else if (*cur == ')' && Top(s) == '(')
			{
				Pop(s);
			}
			else
			{
				printf("括号不匹配\n");
				return;
			}
		}
		++cur;
	}
	if (Empty(s))
		printf("括号匹配\n");
	else
		printf("括号不匹配\n");
}

int main()
{
	Stack s;
	Init(&s);
	char str[20] = "{[(()*)adf]}";
	CheckBrackets(&s, str);
	return 0;
}

队列 Queue （链式存储）

#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <stdbool.h>

typedef int LData;

typedef struct Node
{
	LData data;
	struct Node* next;
}Node;

typedef struct Queue
{
	Node* head;
	Node* tail;
	int size;
}Queue;

void Init(Queue* pq)
{
	assert(pq);
	pq->head = (Node*)malloc(sizeof(Node));
	pq->head->next = NULL;
	pq->tail = pq->head;
	pq->size = 0;
}

bool Empty(Queue* pq)
{
	assert(pq);
	if (pq->head->next == NULL)
		return true;
	return false;
}

void Push(Queue* pq, LData x)
{
	assert(pq);
	Node* new_node = (Node*)malloc(sizeof(Node));
	new_node->data = x;
	new_node->next = NULL;
	pq->tail->next = new_node;
	pq->tail = pq->tail->next;
	++pq->size;
}

void Pop(Queue* pq)
{
	assert(pq);
	assert(!Empty(pq));
	Node* tmp = pq->head;
	pq->head = pq->head->next;
	--pq->size;
	free(tmp);
	tmp = NULL;
}

int Size(Queue* pq)
{
	assert(pq);
	return pq->size;
}

LData Front(Queue* pq)
{
	assert(pq);
	assert(!Empty(pq));
	return pq->head->next->data;
}

void Print(Queue* pq)
{
	assert(pq);
	Node* cur = pq->head->next;
	while (cur != NULL)
	{
		printf("%d ", cur->data);
		cur = cur->next;
	}
	printf("\n");
}

int main()
{
	Queue q;
	Init(&q);
	Push(&q, 1);
	Push(&q, 2);
	Push(&q, 3);
	Push(&q, 4);
	Print(&q);
	Push(&q, Front(&q));
	Pop(&q);
	Pop(&q);
	Pop(&q);
	Print(&q);
	printf("size = %d\n", Size(&q));
}

循环队列 Circle Queue

#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <stdbool.h>

#define CAPACITY 5
typedef int QData;

typedef struct CircleQueue
{
	QData* data;
	int front;
	int tail;
}CircleQueue;

void Init(CircleQueue* pcq)
{
	assert(pcq);
	pcq->data = (QData*)malloc(sizeof(QData) * CAPACITY);
	pcq->front = pcq->tail = 0;
}

bool Empty(CircleQueue* pcq)
{
	assert(pcq);
	if (pcq->front == pcq->tail)
		return true;
	return false;
}

bool Full(CircleQueue* pcq)
{
	assert(pcq);
	if ((pcq->tail + 1) % CAPACITY == pcq->front)
		return true;
	return false;
}

void Push(CircleQueue* pcq, QData x)
{
	assert(pcq);
	assert(!Full(pcq));
	pcq->data[pcq->tail] = x;
	++pcq->tail;
	pcq->tail %= CAPACITY;
}

void Pop(CircleQueue* pcq)
{
	assert(pcq);
	assert(!Empty(pcq));
	++pcq->front;
	pcq->front %= CAPACITY;
}

void Print(CircleQueue* pcq)
{
	assert(pcq);
	int pos = pcq->front;
	while (pos != pcq->tail)
	{
		printf("%d ", pcq->data[pos]);
		++pos;
		pos %= CAPACITY;
	}
	printf("\n");
}

int main()
{
	CircleQueue cq;
	Init(&cq);
	Push(&cq, 1);
	Push(&cq, 2);
	Push(&cq, 3);
	Print(&cq);
	Pop(&cq);
	Pop(&cq);
	Print(&cq);
	Push(&cq, 1);
	Push(&cq, 2);
	Push(&cq, 3);
	Print(&cq);
	return 0;
}

第三章 字符串

• 串是由零个或多个字符组成的顺序存储有限序列
• 串的应用一般包含于<string.h>头文件，常用函数有strlen strcpy strcat strcmp

模拟实现string.h库函数

#include <stdio.h>
#include <assert.h>
#include <stdbool.h>

int MyStrlen(char* str)
{
	assert(str);
	int len = 0;
	char* cur = str;
	while (cur[len++] != '\0'){}
	return len - 1;
}

char* MyStrcpy(char* des, const char* src)
{
	assert(des);
	assert(src);
	char* tmp = des;
	while (*tmp++ = *src++) {}
	return des;
}

char* MyStrcat(char* des, const char* src)
{
	assert(des);
	assert(src);
	char* tmp = des;
	if (des == src)
	{
		int i = 0;
		int len = MyStrlen(src);
		while (*tmp++) {}
		--tmp;
		while (i < len)
		{
			*tmp++ = *src++;
			++i;
		}
		*tmp = '\0';
	}
	else
	{
		while (*tmp++) {}
		--tmp;
		while (*tmp++ = *src++) {}
	}
	return des;
}

int MyStrcmp(const char* str1, const char* str2)
{
	assert(str1);
	assert(str2);
	while (*str1 == *str2)
	{
		if (*str1 == '\0')
			return 0;
		++str1;
		++str2;
	}
	return -(*str1 - *str2);
}

char* MyStrstr(const char* str1, const char* str2)
{
	assert(str1 && str2);
	char* cur = str1;
	while (*cur)
	{
		char* s1 = cur;
		char* s2 = str2;
		while (*s1 && *s2 && *s1 == *s2)
		{
			++s1;
			++s2;
		}
		if (!*s2)
			return cur;
		if (!*s1)
			return NULL;
		++cur;
	}
	return NULL;
}

int main()
{
	char str1[20] = "qwerdf";
	printf("strlen = %d\n", MyStrlen(str1));
	char str2[40];
	printf("str2 strcpy str1 = %s\n", MyStrcpy(str2, str1));
	printf("str2 strcat str1 = %s\n", MyStrcat(str2, str1));
	printf("str2 strcat str2 = %s\n", MyStrcat(str2, str2));
	char str3[40];
	printf("str3 strcmp str2 = %d\n", MyStrcmp(MyStrcpy(str3, str2), str2));
	printf("str1 strstr df = %s\n", MyStrstr(str1, "df"));

	return 0;
}

第四章 广义表

• 广义表中的数据元素可以具有不同的结构（原子或列表），是链式存储结构
• 广义表的第一个元素为表头，其余元素为表尾
• 每个节点可分为表结点或原子节点，用标志位区分
• 表结点包含标志域和指针域（头尾指针），原子节点包含标志域和值域
• 广义表的深度为括号的重数，空表的深度为1，例如X = ((), (e), (a, (b,c,d)))的深度为3
• 广义表的长度为包含的数据元素个数（一个子表只算一个元素）

广义表的实现 利用递归思想

#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <string.h>
#include <malloc.h>

#define AtomType int	//原子类型
typedef enum
{
	HEAD,		//表头结点
	ATOM,		//原子结点
	CHILDLIST	//子表
}ElemTag;

//广义表结点
typedef struct GLNode
{
	ElemTag tag;
	union		//联合体
	{
		AtomType atom;
		struct GLNode* hp;	//表头指针
	};
	struct GLNode* tp;		//表尾指针
}GLNode;

typedef GLNode* GenList;	//广义表

void InitGenList(GenList& gl);
void CreateGenList(GenList& gl, char* str);
bool Sever(char* sub, char* hsub);

char* GetGenListStr(GenList gl, int type);
char* GetHead(GenList gl);
char* GetTail(GenList gl);
char* GetLast(GenList gl);
void ShowGenList(GenList gl);
bool GenListEmpty(GenList gl);
int GenListLength(GenList gl);
int GenListDepth(GenList gl);
void CopyGenList(GenList gl, GenList& T);
void InsertFirstGenList(GenList& gl, char* str);
void DeleteFirstGenList(GenList& gl, char*& str);
void ClearGenList(GenList& gl);
void DestroyGenList(GenList& gl);

//广义表初始化
void InitGenList(GenList& gl)
{
	gl = NULL;
}

//创建广义表：根据字符串创建
void CreateGenList(GenList& gl, char* str)
{
	int n = strlen(str);
	char* sub = (char*)malloc(sizeof(char) * (n - 2));	//存储表内元素
	char* hsub = (char*)malloc(sizeof(char) * (n - 2));	//存储表头
	assert(sub && hsub);
	strncpy(sub, str + 1, n - 2);	//除去字符串两端括号
	sub[n - 2] = '\0';
	if (gl == NULL)		//判空
	{
		gl = (GLNode*)malloc(sizeof(GLNode));
		gl->tag = HEAD;		//标记为头结点
		gl->hp = gl->tp = NULL;	//把子表指针和尾指针都置空
	}
	GLNode* p = gl;
	while (strlen(sub) != 0)
	{
		//尾插法，从后面插入结点
		//	1. 创建一个结点
		//  2. 让p所指节点的尾指针指向新建的结点
		//  3. 让p指向新建节点
		p = p->tp = (GLNode*)malloc(sizeof(GLNode));
		p->hp = p->tp = NULL;
		if (Sever(sub, hsub))	//Sever函数分离表头，并将表头存入hsub中
		{
			if (hsub[0] == '(')
			{
				//创建子表节点
				p->tag = CHILDLIST;	//标记子表
				CreateGenList(p->hp, hsub);
			}
			else
			{
				p->tag = ATOM;	//设置原子标记
				p->atom = atoi(hsub);	//将表头字符串转换成整型并赋值
			}
		}
	}
}

//分离表头，将sub中的表头存入到hsub中
bool Sever(char* sub, char* hsub)
{
	if (*sub == '\0' || strcmp(sub, "()") == 0)
	{
		hsub[0] = '\0';
		return true;
	}
	int n = strlen(sub);
	int i = 0;
	char ch = sub[0];
	int k = 0;	//表示括号信息
	while (i < n && (ch != ',' || k != 0))
	{
		if (ch == '(')
			++k;
		else if (ch == ')')
			--k;
		++i;
		ch = sub[i];
	}
	if (i < n)
	{
		//在 i 位置处截断
		sub[i] = '\0';
		strcpy(hsub, sub);			//将取得的表头放入hsub中
		strcpy(sub, sub + i + 1);	//更新sub：此时的sub是去掉表头hsub
	}
	else if (k != 0)		//判断内部括号是否匹配
		return false;
	else	// i >= n, 整个sub都是表头
	{
		strcpy(hsub, sub);
		sub[0] = '\0';
	}
	return true;
}

//将整数转换成字符串
void NumToStr(int num, char* str, int& i)
{
	char tmp[25];
	_itoa(num, tmp, 10);
	for (unsigned j = 0; j < strlen(tmp); ++j)
		str[i++] = tmp[j];
}

void GetGenList(GenList gl, char* str, int& i)
{
	GLNode* p = gl->tp;
	while (p != NULL)
	{
		if (p->tag == ATOM)
		{
			NumToStr(p->atom, str, i);
			if (p->tp != NULL)
				str[i++] = ',';
			p = p->tp;
		}
		else if (p->tag == CHILDLIST)
		{
			str[i++] = '(';
			GetGenList(p->hp, str, i);
			str[i++] = ')';
			if (p->tp != NULL)
				str[i++] = ',';
			p = p->tp;
		}
	}
}

//将广义表转化成字符串形式
char* GetGenListStr(GenList gl, int type)
{
	int i = 0;
	char* str = (char*)malloc(sizeof(char) * 1000);
	if (type == 0)
	{
		NumToStr(gl->atom, str, i);
	}
	else
	{
		GetGenList(gl, str, i);
	}
	str[i] = '\0';
	return str;
}

//取首元素
char* GetHead(GenList gl)
{
	if (gl->tp->tag == ATOM)
		return GetGenListStr(gl->tp, 0);
	else
		return GetGenListStr(gl->hp, 1);
}

char* GetTail(GenList gl)
{
	GLNode* p = gl->tp;
	if (p->tp != NULL)
		return GetGenListStr(p, 1);
	return NULL;
}

//取最后一个元素
char* GetLast(GenList gl)
{
	GLNode* p = gl->tp;
	while (p->tp != NULL)
		p = p->tp;
	if (p->tag == ATOM)
		return GetGenListStr(p, 0);
	else
		return GetGenListStr(p->hp, 1);
}

//打印广义表
void ShowGenList(GenList gl)
{
	printf("(%s)", GetGenListStr(gl, 1));
}

//判空
bool GenListEmpty(GenList gl)
{
	return gl->tp == NULL;
}

int GenListLength(GenList gl)
{
	int length = 0;
	GLNode* p = gl->tp;
	while (p != NULL)
	{
		++length;
		p = p->tp;
	}
	return length;
}

int GenListDepth(GenList gl)
{
	if (gl->tp == NULL)
		return 1;
	GLNode* p = gl->tp;
	int maxdepth = 0;
	int dep;
	while (p != NULL)
	{
		if (p != NULL)
		{
			if (p->tag == CHILDLIST)
			{
				dep = GenListDepth(p->hp);
				if (dep > maxdepth)
					maxdepth = dep;
			}
		}
		p = p->tp;
	}
	return maxdepth + 1;
}

//广义表复制
void CopyGenList(GenList gl, GenList& T)
{
	if (gl == NULL)
		return;
	if (T != NULL)
		DestroyGenList(T);
	T = (GLNode*)malloc(sizeof(GLNode));
	T->tag = gl->tag;
	T->hp = gl->hp;
	T->tp = gl->tp;
	GLNode* p = gl->tp;
	GLNode* q = T;
	while (p != NULL)
	{
		q = q->tp = (GLNode*)malloc(sizeof(GLNode));
		q->tag = p->tag;
		q->hp = q->tp = NULL;
		if (p->tag == ATOM)
		{
			q->atom = p->atom;
			p = p->tp;
		}
		else if (p->tag == CHILDLIST)
		{
			CopyGenList(p->hp, q->hp);
			p = p->tp;
		}
	}
}

//插入元素str
void InsertFirstGenList(GenList& gl, char* str)
{
	GenList t;
	InitGenList(t);
	CreateGenList(t, str);
	GLNode* p = t->tp;
	while (p->tp != NULL)
		p = p->tp;
	p->tp = gl->tp;
	gl->tp = t->tp;
	free(t);
}

//删除广义表第一个位置的元素
void DeleteFirstGenList(GenList& gl, char*& str)
{
	GenList t;
	InitGenList(t);
	t = gl->tp;
	gl->tp = gl->tp->tp;
	if (t->tag == CHILDLIST)
	{
		str = GetGenListStr(t->hp, 1);
		DestroyGenList(t->hp);
	}
	else if (t->tag == ATOM)
	{
		str = GetGenListStr(t, 0);
	}
	free(t);
}

//清空广义表
void ClearGenList(GenList& gl)
{
	GLNode* p = gl->tp;
	while (p != NULL)
	{
		if (p->tag == ATOM)
		{
			gl->tp = p->tp;
			free(p);
			p = gl->tp;
		}
		else if (p->tag == CHILDLIST)
		{
			ClearGenList(p->hp);
			p = p->tp;
		}
	}
}

//销毁
void DestroyGenList(GenList& gl)
{
	ClearGenList(gl);
	free(gl);
	gl = NULL;
}

//测试
int main()
{
	GenList gl;
	InitGenList(gl);

	char ga[30] = "(1,2,3)";
	char gb[30] = "(1,(2,3))";
	char gc[30] = "(1,(2,3),4)";
	char gd[30] = "((1,2),3)";
	char ge[30] = "((1,2,3))";
	char gf[30] = "()";
	char gg[30] = "(1,(2,(3,(10,20),4),5),6)";
	char gh[30] = "((((1,2),1),1),6,1)";

	CreateGenList(gl, gg);
	ShowGenList(gl);
	printf("\n");
	int length = GenListLength(gl);
	printf("length = %d\n", length);

	int depth = GenListDepth(gl);
	printf("depth = %d\n", depth);

	GenList T;
	InitGenList(T);
	printf("----------------------------\n");
	printf("复制：");
	CopyGenList(gl, T);
	ShowGenList(T);
	printf("\n");

	printf("----------------------------\n");
	printf("插入前：");
	ShowGenList(gl);
	printf("\n");
	InsertFirstGenList(gl, ga);
	printf("插入后：");
	ShowGenList(gl);
	printf("\n");
	printf("----------------------------\n");
	char* str;
	printf("删除前：");
	ShowGenList(gl);
	printf("\n");
	DeleteFirstGenList(gl, str);
	printf("删除后：");
	ShowGenList(gl);
	printf("\n");
	printf("删除的首元素为：%s\n", str);

	printf("----------------------------\n");
	ShowGenList(gl);
	printf("\n");
	printf("头元素为：%s\n", GetHead(gl));
	printf("尾元素为：%s\n", GetTail(gl));

	DestroyGenList(gl);
	return 0;
}

第五章 树

• 树是有n个节点的有限集，任意一棵非空树有且仅有一个根节点
• 拥有的分支数称为节点的度，度为0的节点为叶子节点
• 森林是若干棵互补相交的树的集合

二叉树：

• 二叉树每个节点的度 ≤ 2，分左右孩子
• 二叉树的第 i 层最多有 2^(i-1) 个节点
• 当深度为 k 的二叉树有 2^k - 1 个节点时是满二叉树
• 当k-1层是满的，第k层是连续的节点时是完全二叉树
• 具有 n 个节点的满二叉树的深度 h = log2(n+1)
• 任一二叉树，设叶节点数为n0，度为2的节点数为n2，则 n0 = n2 + 1
• 遍历二叉树分为先序遍历(根左右)、中序遍历(左根右)、后序遍历(左右根)、层序遍历
• 任一具有n个节点的树，其分支有n-1条

 二叉树与森林的转换：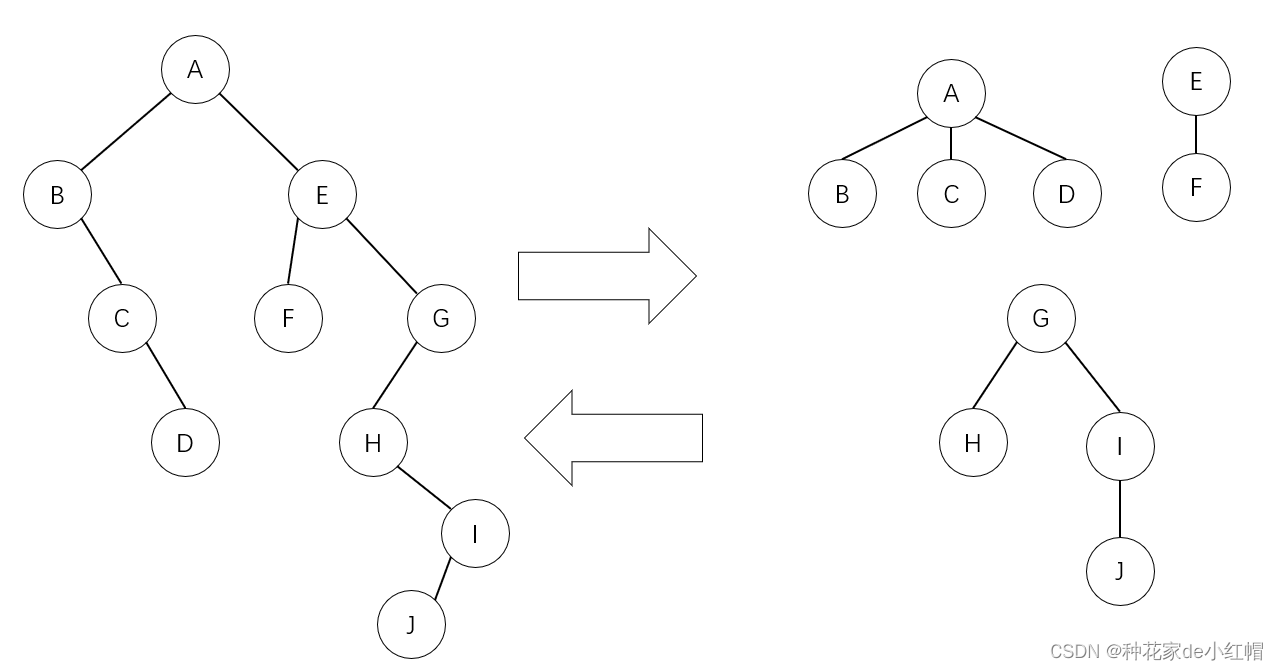

赫夫曼树：

• 赫夫曼树，又称最优树，是一类带权路径最短的树
• 路径长度：路径上的分支数目
• 树的带权路径长度：所有叶子节点的带权路径长度之和

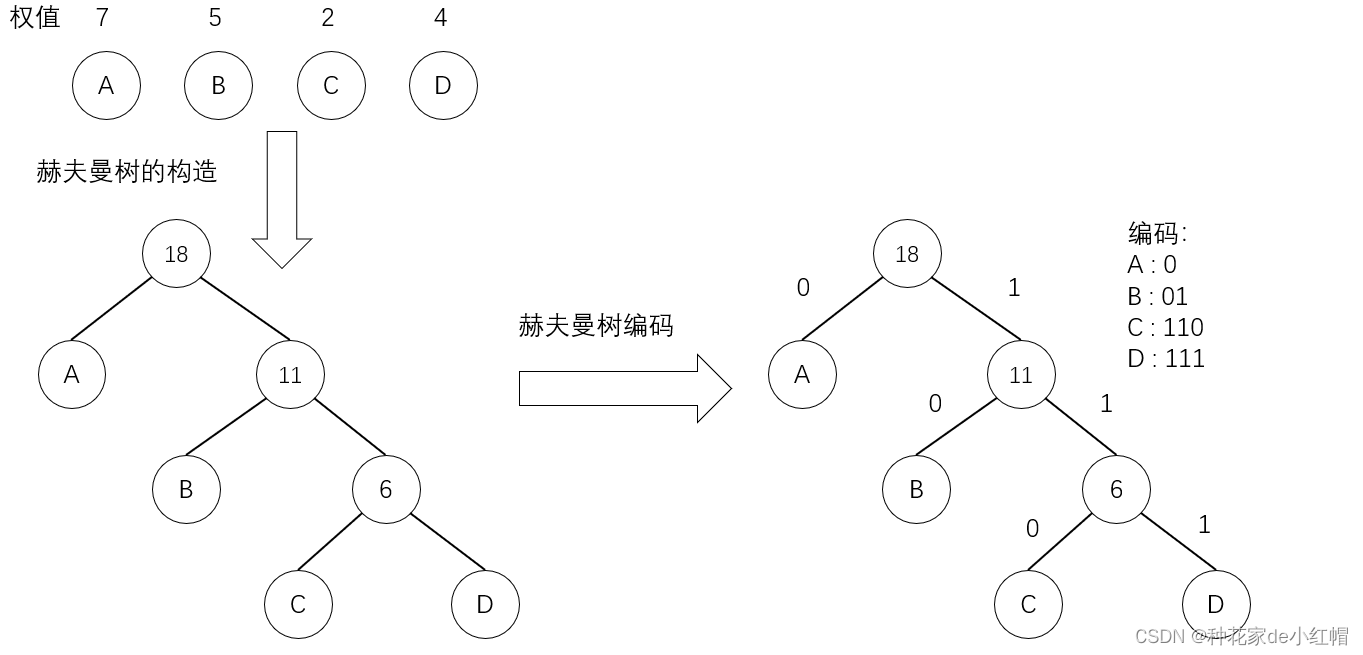
二叉树的构建与遍历 递归思想

#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <stdbool.h>

typedef char NodeType;

typedef struct BNTree
{
	NodeType data;
	struct BNTree* left;
	struct BNTree* right;
}BNTree;

BNTree* BuyNode(NodeType d)			//开辟一个二叉树节点
{
	BNTree* new_node = (BNTree*)malloc(sizeof(BNTree));
	new_node->data = d;
	new_node->left = new_node->right = NULL;
	return new_node;
}

BNTree* CreateBNTree(NodeType* d, int* pi)		//二叉树创建
{
	if (d[*pi] = '#')
	{
		(*pi)++;
		return NULL;
	}
	BNTree* root = BuyNode(d[(*pi)++]);			//先序构建
	root->left = CreateBNTree(d, pi);
	root->right = CreateBNTree(d, pi);
	return root;
}

void PreOrder(BNTree* root)	//先序遍历，中序遍历和后续遍历都是一样的递归思想
{
	if (root == NULL)
		return;
	printf("%c ", root->data);
	PreOrder(root->left);
	PreOrder(root->right);
}

第六章 图

图是一种抽象数据类型，图的元素被称为顶点，顶点之间可能存在相关关系，一个图G包含一个顶点集V和关系集VR，记为：G = (V, VR)

（一）图的常用术语

1. 有向图、弧

• 若图G中的两个顶点a、b的关系为有序对<a,b>，<a,b>∈VR，则称<a,b>为有向图G的一条弧
• 在弧<a,b>中，a是弧尾（初始点），b是弧头（终止点）
• 有向图是由顶点集和弧集组成的二元集合

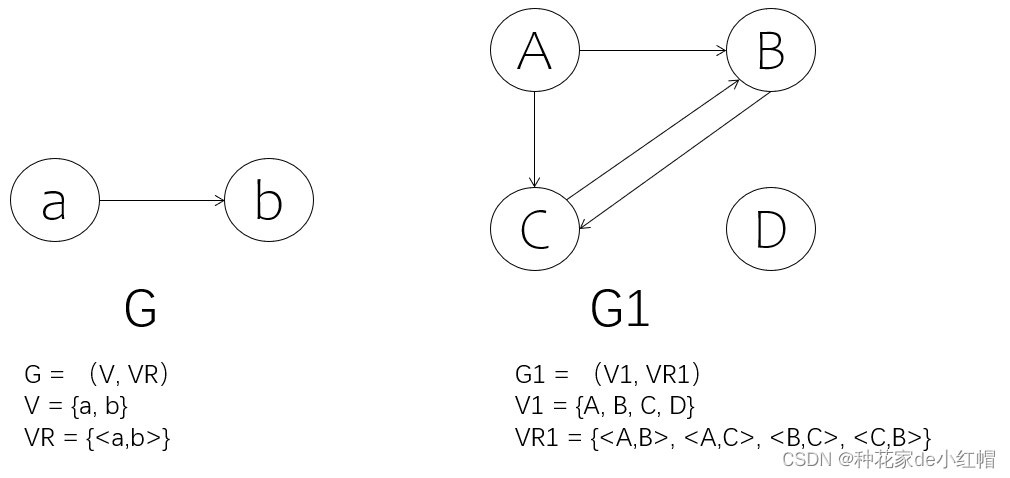
2. 无向图、边

• 若图G中的两个顶点a、b的关系为无序对(a,b)，(a,b)∈VR，则称(a,b)为无向图G的一条边
• 若顶点a、b间有边，则(a,b)表示a、b互为邻接点，边(a,b)依附于顶点a、b

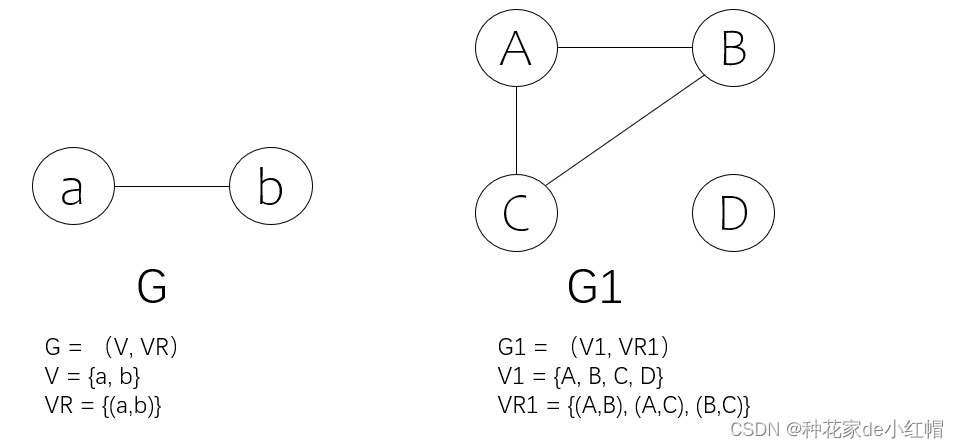
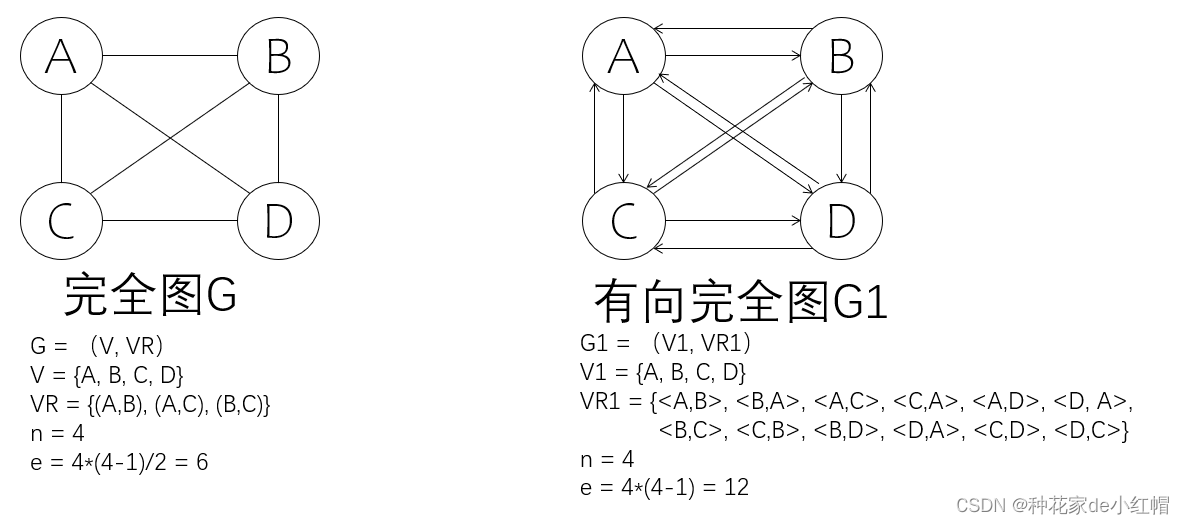
3. 完全图、有向完全图

• n：顶点的数目
• e：边或弧的数目
• 若边数 e = n*(n-1)/2 的无向图，则称为完全图，表示任意两个顶点间都有边
• 若弧数 e = n*(n-1) 的有向图，则称有向完全图，表示任意两个顶点间都有两条弧

4. 网

• 弧（边）上加权的图，分为有向网和无向网
• 故有四种类型的图：有向图、无向图、有向网、无向网

5. 子图

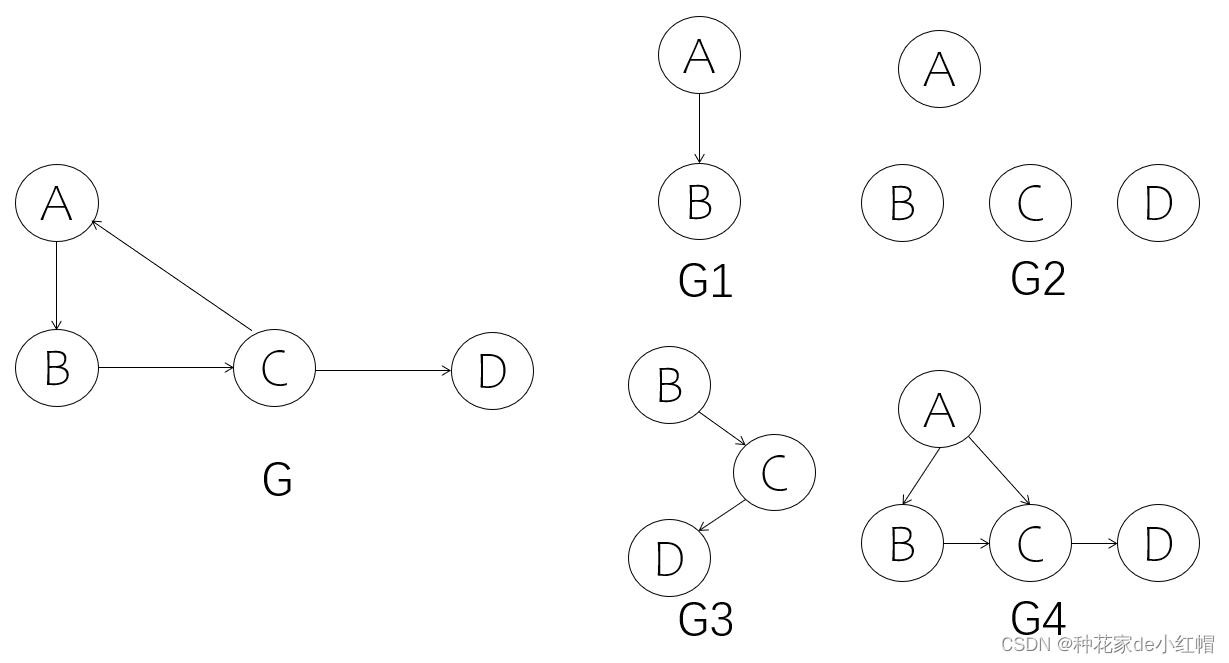
• 对图G=(V, VR)，G1=(V1, VR1)，若V1∈V且VR1∈VR，则G1是G的子图
• 下例中G1、G2、G3都是G的子图，G4不是G的子图

6. 度、出度、入度

• 度D(TD)：图中与某顶点相关的边(弧)的数目，称为某顶点的度
• 无向图中某顶点的度表示该顶点有多少个邻接点
• 出度OD：有向图中以某顶点为弧尾的弧的数目
• 入度ID：有向图中以某顶点为弧头的弧的数目
• 有向图某顶点的度 D = OD + ID

7. 连通性

• 从顶点vi到顶点vj有路径，则称二者是连通的
• 连通图：图中任意两个顶点都是连通的
• 完全图一定是连通图，连通图不一定是完全图
• 连通分量：无向图的极大连通子图，连通图的连通分量是自己本身
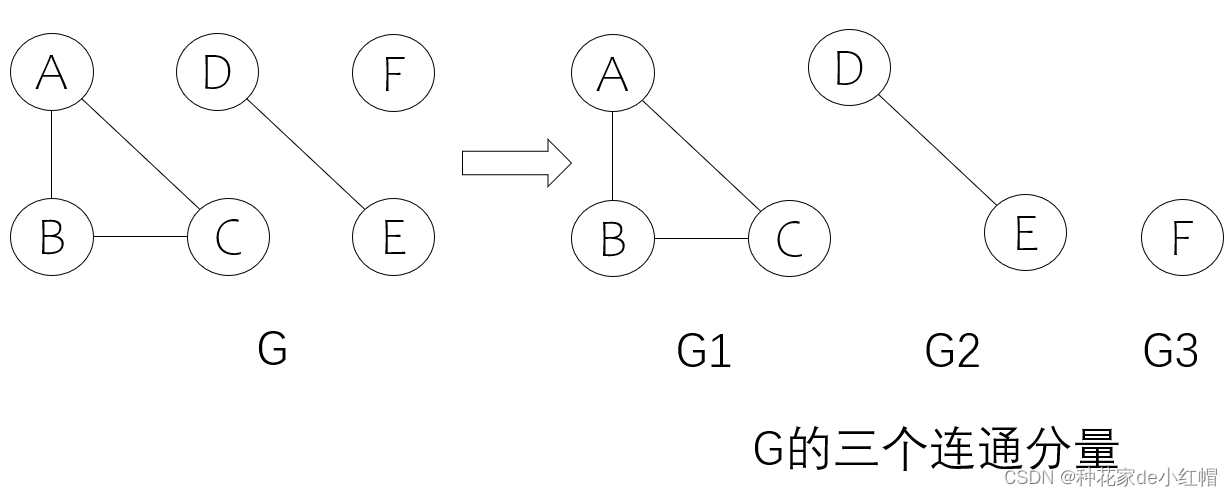
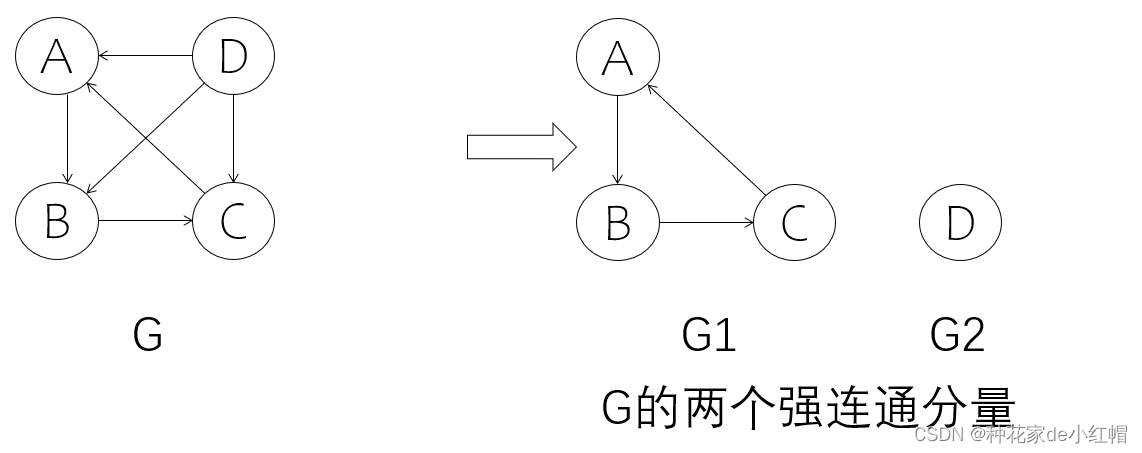
• 强连通图：有向图中任意两个顶点vi和vj之间，从vi到vj和从vj到vi之间都存在路径
• 强连通分量：有向图的极大强连通子图，强联通图的强连通分量是自己本身

8. 生成树

• 一个连通图的生成树是一个极小连通子图
• 生成树含有图中的全部n个顶点，但有且仅有n-1条边
• 如果在生成树上再添加一条边，必定构成一个环，不再是树结构
• 一个有n个顶点的图，如果边数小于n-1，则一定是非连通图，如果多于n-1条边，则一定有环
• 有n-1条边的图不一定是生成树
• 一个连通图可以有多颗生成树

（二）图的存储结构

1. 数组表示

• 用两个数组分别存储数据元素的信息和数据元素之间的关系
• 顶点数组：用一维数组存储顶点
• 关系数组：用二维数组存储顶点之间的关系

（1）无向图

• 顶点数组vexs：V = {v0, v1, v2, v3}
• 关系数组（邻接矩阵arcs）：1表示顶点之间有关系，0表示顶点之间无关系
• 邻接矩阵arcs：VR = {(v0,v2), (v0,v3), (v2,v3)}
• 无向图的邻接矩阵是对称矩阵
• 顶点 vi 的度为第 i 行或第 i 列的和

（2）有向图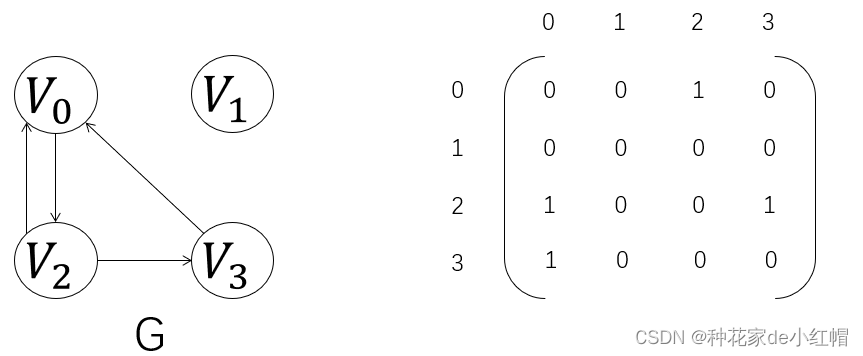

• 顶点数组vexs：V = {v0, v1, v2, v3}
• 邻接矩阵arcs：VR = {<v0,v2>, <v2,v0>, <v2,v3>, <v3,v0>}
• 有向图的邻接矩阵不一定是对称矩阵
• 顶点 vi 的度为第 i 行和第 i 列的和，即 D = OD + ID

2. 邻接表

顺序+链式存储结构，通过头结点数组保存顶点信息，用单链表保存顶点之间的关系

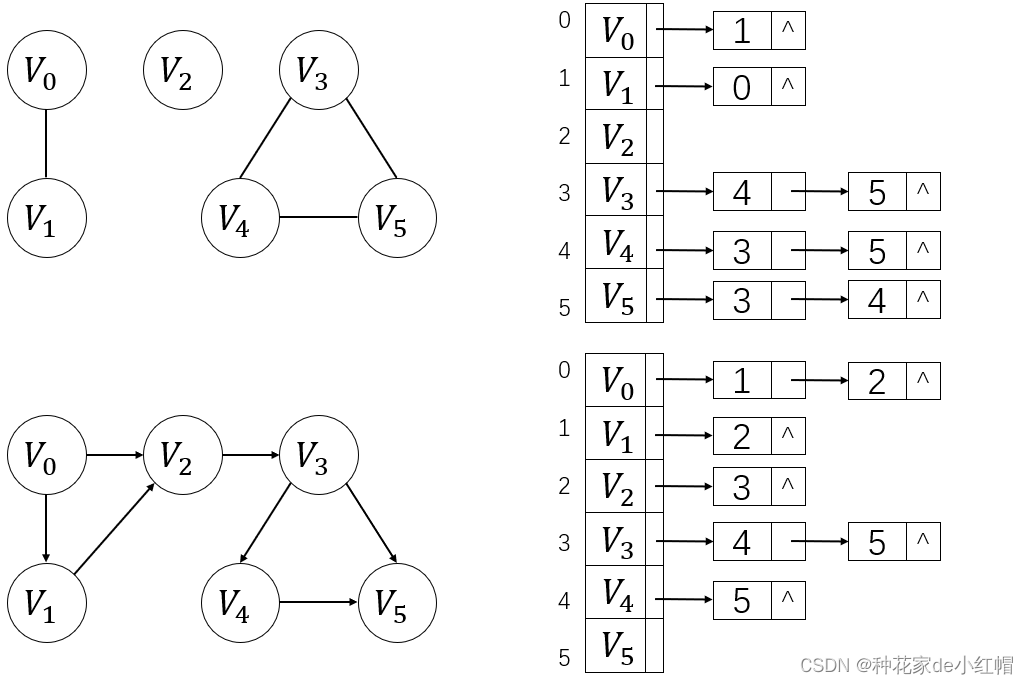
无向图：

• 图G的每个顶点建立一个单链表，第 i 个单链表中的结点表示依附于 vi 的边
• 若有 n 个顶点和 c 条边，则有 n 条单链表和 2*c 个表结点
• 顶点 vi 的度 = 第 i 个单链表的长度

有向图：

•  图G中的每个顶点建立一个单链表，第 i 条链表中的表结点值为 j ，表示<vi, vj>
• 若有 n 个顶点和 c 条弧，则有 n 条单链表和 c 个表结点
• 顶点 vi 的度 = 第 i 个单链表的长度

3. 十字链表

十字链表是针对有向图设计的邻接表和逆邻接表的组合

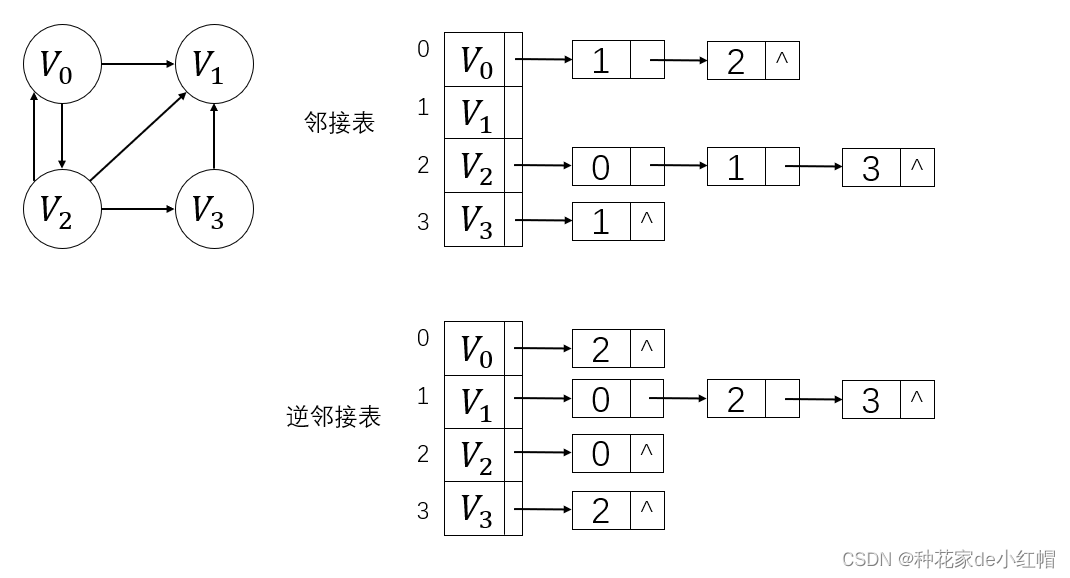
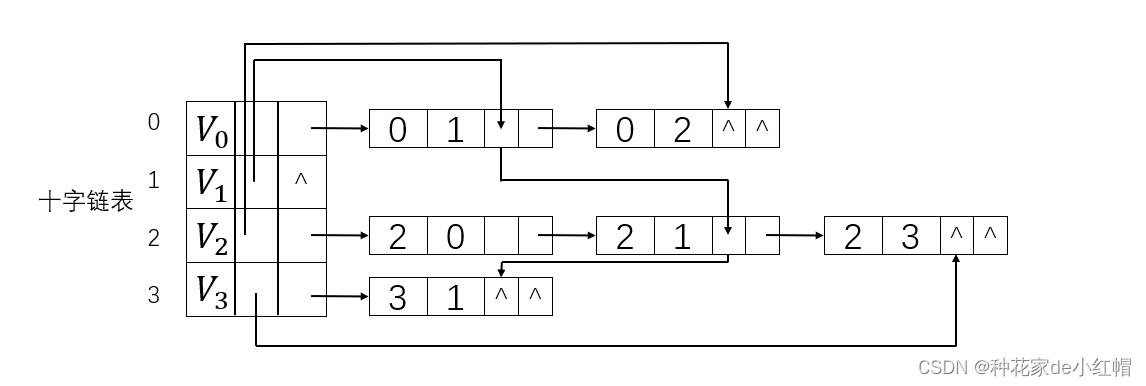
• 每个顶点有一个顶点结点，顶点结点包括：data(顶点信息)、first_in(指向以该顶点为弧头的第一条弧)、first_out(指向以该顶点为弧尾的第一条弧)
• 每条弧有一个弧结点，若 vi 到 vj 有弧，则弧结点包括：tail_vec(弧尾位置)、head_vec(弧头位置)、h_link(指向下一条弧头(vi)相同的弧)、t_link(指向下一条弧尾(vi)相同的弧)
• n条弧就有n个链表结点

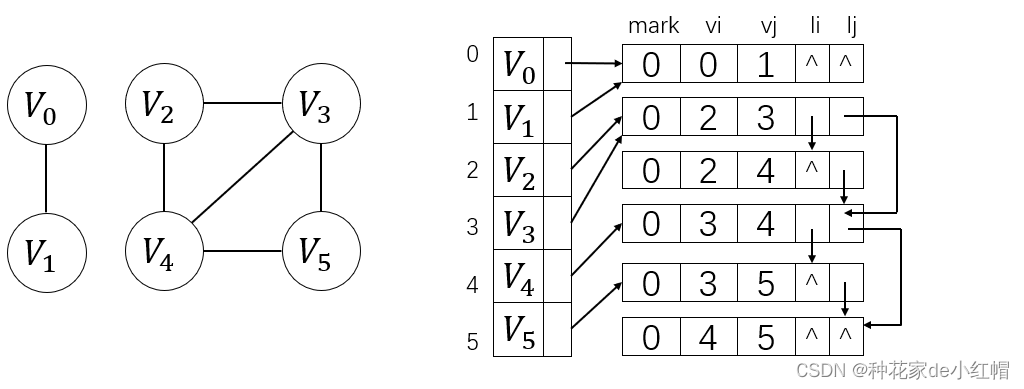
4. 邻接多重表（无向图）

• 每个顶点有一个头结点，顶点节点包括：data(顶点信息)、first_edge(指向第一条依附于该顶点的边)
• 每一条边都有一个表结点，表结点包括：mark(标志域，标记该边是否被搜索过)、vi / vj(依附于该边的两个顶点位置)、li(指向下一条依附于顶点vi的边)、lj(指向下一条依附于顶点vj的边)
• n条边就有n个表结点

第七章 查找

折半查找（二分查找）：针对有序数列，时间复杂度为O(lgN)

二叉排序树（二叉查找树）：若左子树非空，则左子树上所有杰点都小于它的根结点；若右子树非空，则右子树上所有结点都大于它的根结点

平衡二叉树（AVL树）：左子树和右子树的深度之差的绝对值（平衡因子）不超过1，某结点的平衡因子为其左子树的深度减去右子树的深度

二叉排序树的构建：

#include <iostream>
#include <queue>
using namespace std;

typedef struct Node
{
	int data;
	struct Node* left;
	struct Node* right;
}Node;

void BuyNode(Node*& t, int x)
{
	t = new Node;
	t->data = x;
	t->left = t->right = NULL;
}

void CreateBTree(Node*& t, int x)
{
	if (t == NULL)
	{
		BuyNode(t, x);
		return;
	}
	if (x < t->data)
		CreateBTree(t->left, x);
	else
		CreateBTree(t->right, x);
}

void PrintBTree(Node* t)
{
	Node* p = t;
	queue<Node*> q;
	q.push(p);
	while (!q.empty())
	{
		p = q.front();
		q.pop();
		cout << p->data << ' ';
		if (p->left != NULL)
			q.push(p->left);
		if (p->right != NULL)
			q.push(p->right);
	}
}

int main()
{
	int n;
	while (cin >> n)
	{
		Node* t = NULL;
		for (int i = 0; i < n; ++i)
		{
			int a;
			cin >> a;
			CreateBTree(t, a);
		}
		PrintBTree(t);
		cout << endl;
	}
}

B-树（平衡多路查找树）：常应用于文件系统，一棵m阶的B-树，或为空树，或遵循下列条件：

• 树中的每个结点最多有m棵子树
• 若根结点不是叶子结点，则至少有两棵子树
• 除根结点外，所有非终端结点至少有 m/2 棵
• 所有非终端结点包含如下信息：（n, A0,K1, A1, K2, A2......Kn, An）, Ki为关键码
• 所有叶子结点都出现在同一层次上，且不带信息

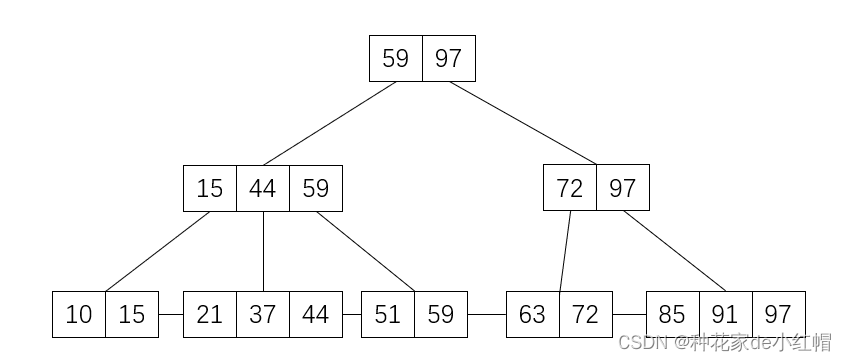
要在如上4阶B-树中查找45这个树的步骤：

• 首先从根结点开始，45 > 35，往右子树走，到结点c
• 结点c有两个关键字，43 < 45 < 78，故往中间的子树走，到结点g
• 结点g有三个关键字，45 < 47，往最左边子树走，到叶子结点F，故45不在B-树中

B-树的插入：

• 用查找的方法找出关键字的插入位置，若查找到了这个数，则直接返回
• 判断插入位置的结点是否满足 n <= m-1 ，若满足则直接插入，若不满足则进行分裂
• 分裂规则是左右两边的数分裂成不同结点，中间的数移到父结点，再检查父结点是否满足阶数规则

B-树的删除：

• 先直接删除，再视情况进行调整，以满足阶数规则

B+树：

一棵m阶的B+树与m阶的B-树的差异：

• 有n棵子树的结点有n个关键字
• 所有关键字信息都在叶子节点中，叶子结点本身依关键字顺序存储
• 所有非终端结点都是索引部分，结点中只含有其子树（根结点）最大（或最小）的关键字
• B+树的查找，不管成功与否，每次都是从根到叶子结点的路径

哈希表：若结构中存在关键字和K相等的记录，则必定在 f(K) 的存储位置上，由此不需比较便可直接取得所查记录，因此这个对应关系 f 为哈希函数，这个思维建立的表为哈希表

第八章 内排序

直接插入排序

void InsertSort(int* arr, int n)
{
	int i;
	for (i = 0; i < n - 1; ++i)
	{
		int end = i;
		int tmp = arr[end + 1];
		while (end >= 0 && tmp < arr[end])
		{
			arr[end + 1] = arr[end];
			--end;
		}
		arr[end + 1] = tmp;
	}
}

希尔排序

• 第一步：预排序
• 第二步：直接插入排序

void ShellSort(int* arr, int n)
{
	int gap = n;
	while (gap > 1)
	{
		gap = gap / 3 + 1;
		int i;
		for (i = 0; i < n - gap; ++i)
		{
			int end = i;
			int tmp = arr[end + gap];
			while (end >= 0 && tmp < arr[end])
			{
				arr[end + gap] = arr[end];
				end -= gap;
			}
			arr[end + gap] = tmp;
		}
	}
}

直接选择排序

void SelectSort(int* arr, int n)
{
	int begin = 0;
	int end = n - 1;
	while (begin < end)
	{
		int mini = begin;
		int maxi = end;
		int i;
		for (i = begin + 1; i <= end; ++i)
		{
			if (arr[i] > arr[maxi])
				maxi = i;
			else if (arr[i] < arr[mini])
				mini = i;
		}
		int tmp = arr[begin];
		arr[begin] = arr[mini];
		arr[mini] = tmp;
		if (maxi == begin)
			maxi = mini;
		int temp = arr[end];
		arr[end] = arr[maxi];
		arr[maxi] = temp;
		++begin;
		--end;
	}
}

堆排序

//建立大根堆——升序
//建立小根堆——降序
void AdjustDown(int* arr, int size, int parent)
{
	int child = parent * 2 + 1;
	while (child < size)
	{
		if (child + 1 < size && arr[child + 1] > arr[child])
			++child;
		if (arr[parent] < arr[child])
		{
			int tmp = arr[parent];
			arr[parent] = arr[child];
			arr[child] = tmp;
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

void HeapSort(int* arr, int n)
{
	int parent = (n - 1 - 1) / 2;
	while (parent >= 0)
	{
		AdjustDown(arr, n, parent);
		--parent;
	}
	while (n > 1)
	{
		int tmp = arr[0];
		arr[0] = arr[n - 1];
		arr[n - 1] = tmp;
		AdjustDown(arr, n - 1, 0);
		--n;
	}
}

冒泡排序

void BubbleSort(int* arr, int n)
{
	int i, j;
	for (i = 0; i < n; ++i)
	{
		int flag = 0;
		for (j = 0; j < n - 1 - i; ++j)
		{
			if (arr[j + 1] < arr[j])
			{
				int tmp = arr[j + 1];
				arr[j + 1] = arr[j];
				arr[j] = tmp;
				flag = 1;
			}
		}
		if (flag == 0)
			break;
	}
}

快速排序

第一步：找到一个值key（默认将key值设为数组第一个元素）

第二步：用循环将比key值小的放key值左边，比key值大的放key值右边

第三步：用递归（二叉树的分治算法），将key值的左右分为两个子树进行排序

//三数取1，取中位数
int GetMidIndex(int* arr, int begin, int end)
{
	int midi = (begin + end) / 2;
	if (arr[begin] < arr[end])
	{
		if (arr[midi] < arr[begin])
			return begin;
		else if (arr[midi] < arr[end])
			return midi;
		else
			return end;
	}
	else
	{
		if (arr[midi] > arr[begin])
			return begin;
		else if (arr[midi] > arr[end])
			return midi;
		else
			return end;
	}
}

int PtrPartSort(int* arr, int begin, int end)
{
	int keyi = begin;
	int pre = begin;
	int cur = begin + 1;
	int midi = GetMidIndex(arr, begin, end);
	int tmp = arr[keyi];
	arr[keyi] = arr[midi];
	arr[midi] = tmp;
	while (cur <= end)
	{
		if (arr[cur] < arr[keyi] && pre++ != cur)
		{
			int temp = arr[cur];
			arr[cur] = arr[pre];
			arr[pre] = temp;
		}
		++cur;
	}
	int t = arr[keyi];
	arr[keyi] = arr[pre];
	arr[pre] = t;
	return pre;
}

void QuickSort(int* arr, int begin, int end)
{
	if (begin >= end)
		return;
	int keyi = PtrPartSort(arr, begin, end);
	if (begin - end > 10)
	{
		QuickSort(arr, begin, keyi - 1);
		QuickSort(arr, keyi + 1, end);
	}
	else
	{
		InsertSort(arr + begin, end - begin + 1);
	}
}

归并排序

void _MergeSort(int* arr, int begin, int end, int* tmp)
{
	if (begin >= end)
		return;
	int mid = (begin + end) / 2;
	_MergeSort(arr, begin, mid, tmp);
	_MergeSort(arr, mid + 1, end, tmp);
	int begin1 = begin, end1 = mid;
	int begin2 = mid + 1, end2 = end;
	int i = begin;
	while (begin1 <= end1 && begin2 <= end2)
	{
		if (arr[begin1] < arr[begin2])
			tmp[i++] = arr[begin1++];
		if (arr[begin1] > arr[begin2])
			tmp[i++] = arr[begin2++];
	}
	while (begin1 <= end1)
	{
		tmp[i++] = arr[begin1++];
	}
	while (begin2 <= end2)
	{
		tmp[i++] = arr[begin2++];
	}
	memcpy(arr + begin, tmp + begin, sizeof(int) * (end - begin + 1));
}

void MergeSort(int* arr, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL)
	{
		perror("malloc");
		exit(-1);
	}
	_MergeSort(arr, 0, n - 1, tmp);
	free(tmp);
}

计数排序

void NumSort(int* arr, int n)
{
	int min = arr[0];
	int max = arr[0];
	int i;
	for (i = 1; i < n; ++i)
	{
		if (arr[i] < min)
			min = arr[i];
		if (arr[i] > max)
			max = arr[i];
	}
	int* count = (int*)malloc(sizeof(int) * (max - min + 1));
	memset(count, 0, sizeof(int) * (max - min + 1));
	for (i = 0; i < n; ++i)
	{
		count[arr[i] - min]++;
	}
	int j = 0;
	for (i = 0; i <= max - min; ++i)
	{
		while (count[i]--)
		{
			arr[j++] = min + i;
		}
	}
	free(count);
	count = NULL;
}

基数排序

#include <iostream>
#include <queue>
#include <iomanip>
using namespace std;

#define K 3
#define RADIX 10

int GetKey(int value, int k)
{
	int key = 0;
	while (k >= 0)
	{
		key = value % 10;
		value /= 10;
		--k;
	}
	return key;
}

queue<int> Q[RADIX];	//定义基数

void Distribute(int* arr, int left, int right, int k)
{
	for (int i = left; i < right; ++i)
	{
		int key = GetKey(arr[i], k);
		Q[key].push(arr[i]);
	}
}

void Collect(int* arr)
{
	int k = 0;
	for (int i = 0; i < RADIX; ++i)
	{
		while (!Q[i].empty())
		{
			arr[k++] = Q[i].front();
			Q[i].pop();
		}
	}
}

void RadixSort(int* arr, int left, int right)
{
	for (int i = 0; i < K; ++i)
	{
		Distribute(arr, left, right, i);
		Collect(arr);
	}
}

void PrintArr(int* arr, int n)
{
	int i = 0;
	for (; i < n; ++i)
		printf("%d ", arr[i]);
	printf("\n");
}

int main()
{
	int arr[20] = { 11, 333, 521, 71, 19, 2, 432, 61, 38, 120, 0 };

	RadixSort(arr, 0, 11);
	PrintArr(arr, 11);

	return 0;
}