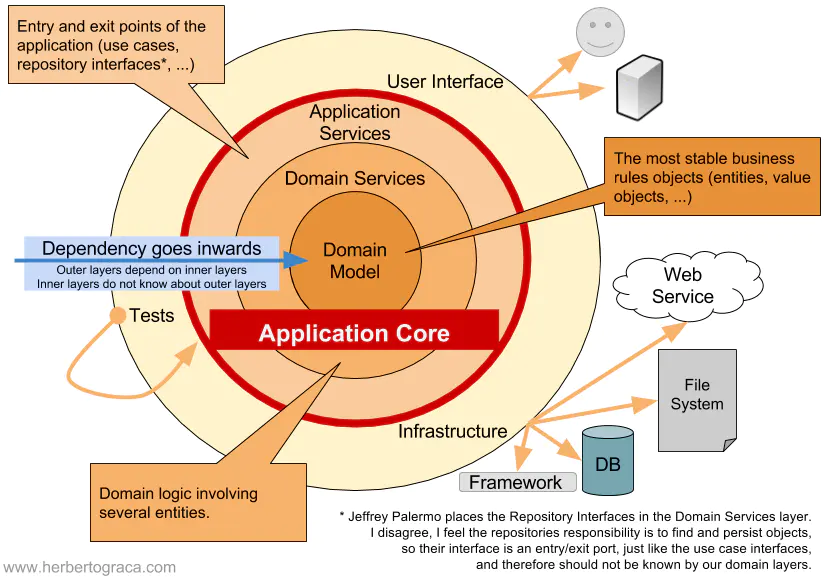
对于有些矩阵,矩阵中某个元素的一个很小的变动,会引起最后计算结果误差很大,这种矩阵称为“病态矩阵”。有些时候不正确的计算方法也会使一个正常的矩阵在运算中表现出病态。对于高斯消去法来说,如果主元(即对角线上的元素)上的元素很小,在计算时就会表现出病态的特征。
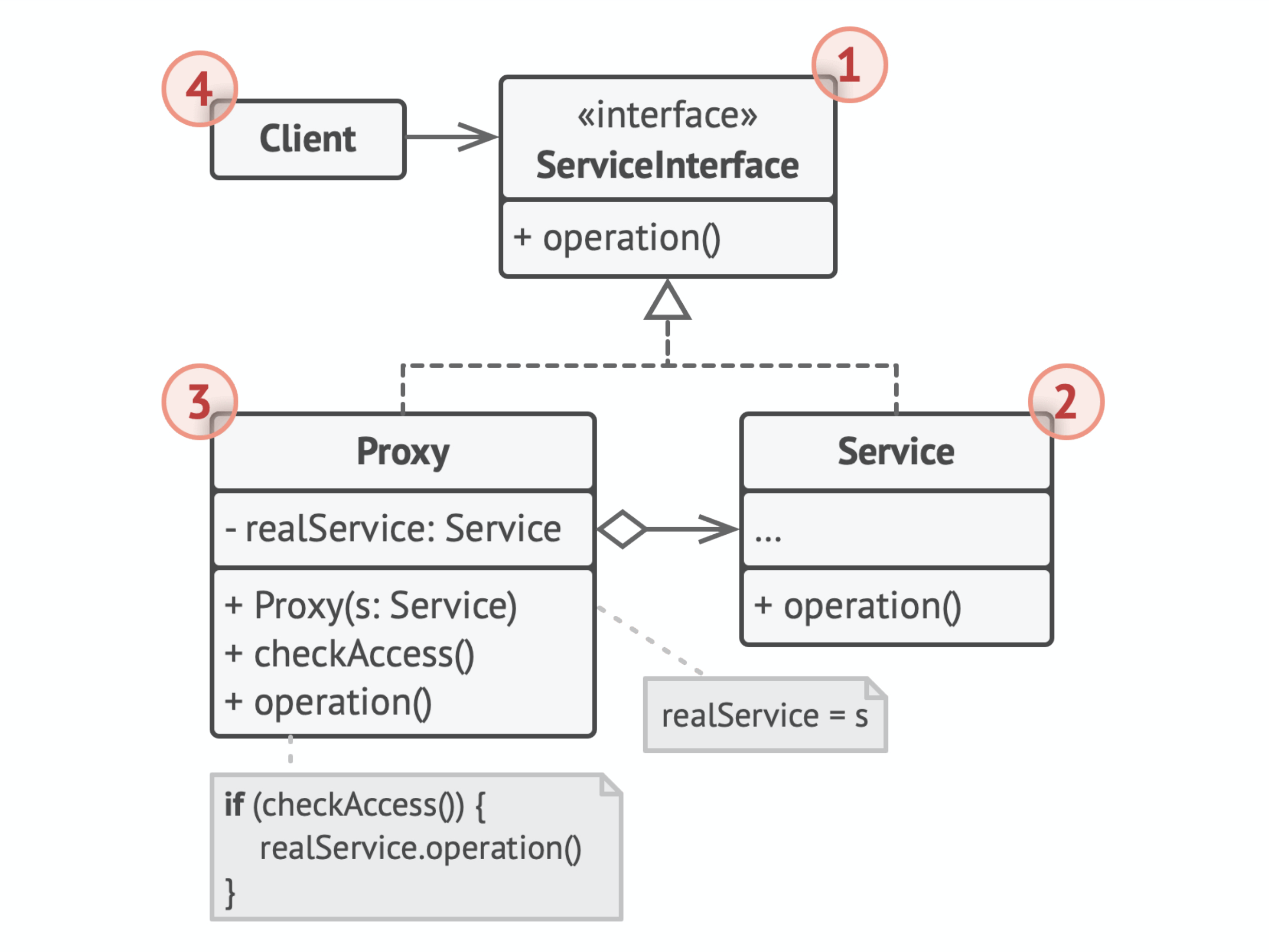
回归分析中常用的最小二乘法是一种无偏估计。对于一个适定问题,X通常是列满秩的
![]()
采用最小二乘法,定义损失函数为残差的平方,最小化损失函数
![]()
上述优化问题可以采用梯度下降法进行求解,也可以采用如下公式进行直接求解
![]()
当X不是列满秩时,或者某些列之间的线性相关性比较大时,X的转置和X相乘的行列式接近于0,即结果接近于奇异,上述问题变为一个不适定问题,此时,计算结果的逆时误差会很大,传统的最小二乘法缺乏稳定性与可靠性。为了解决上述问题,我们需要将不适定问题转化为适定问题:我们为上述损失函数加上一个正则化项,变为
![]()
其中,我们定义
![]()
,于是:
![]()
上式中,I是单位矩阵。随着alpha 的增大,theta(alpha) 各元素 的绝对值均趋于不断变小,它们相对于正确值theta(i) 的偏差也越来越大。
alpha 趋于无穷大时,theta(alpha) 趋于0。其中,theta(alpha) 随alpha 的改变而变化的轨迹,就称为岭迹。实际计算中可选非常多的alpha 值,做出一个岭迹图,看看这个图在取哪个值的时候变稳定了,那就确定alpha值了。
岭回归是对最小二乘回归的一种补充,它损失了无偏性,来换取高的数值稳定性,从而得到较高的计算精度。
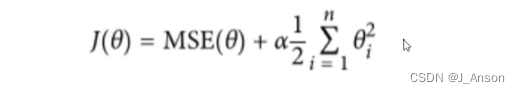
sklearn中的Ridge内置支持多元回归(即,当 y 是形状为 (n_samples, n_targets) 的二维数组时)。岭回归模型用于求解回归模型,其中损失函数是线性最小二乘函数,正则化由 l2-norm给出,也称岭回归为吉洪诺夫正则化。
岭回归,即对每一个theta(i)增加他的平方项。本次实验,我们来观察不同的alpha值对每一个产生的theta结果的影响。
一、导入包
import matplotlib.pyplot as plt
import numpy as np
from sklearn.linear_model import Ridge
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures, StandardScaler二、准备数据
np.random.seed(42)
m = 20
X = 3 * np.random.rand(m, 1)
y = 0.5 * X + np.random.rand(m, 1) / 1.5 + 1三、查看数据分布情况
plt.plot(X, y, "b.")
plt.xlabel("X")
plt.ylabel("y")
plt.axis([0, 3, 0, 3])
plt.show()
四、定义岭回归函数对比
通过polynomial参数判断是否采用流水线方式开展多项式特征生成和数据标准化
def plot_model(model_class, data_X, polynomial, alphas, **model_kargs):
for alpha, style in zip(alphas, ("b-", "g--", "r:")):
model = model_class(alpha, **model_kargs)
if polynomial:
model = Pipeline([
("poly_features", PolynomialFeatures(degree=10, include_bias=False)),
("StandardScaler", StandardScaler()),
("lin_reg", model)])
model.fit(X, y)
y_new_regul = model.predict(data_X)
lw = 2 if alpha > 0 else 1
plt.plot(data_X, y_new_regul, style, linewidth=lw, label=f"alpha={alpha}")
plt.plot(X, y, "b.", linewidth=3)
plt.legend()五、画图
X_new = np.linspace(0, 3, 100).reshape(100, 1)
plt.figure(figsize=(10, 5))
plt.subplot(121)
plot_model(Ridge, data_X=X_new, polynomial=False, alphas=(0, 10, 100))
plt.subplot(122)
plot_model(Ridge, data_X=X_new, polynomial=True, alphas=(0, 10 ** -5, 1))
plt.show()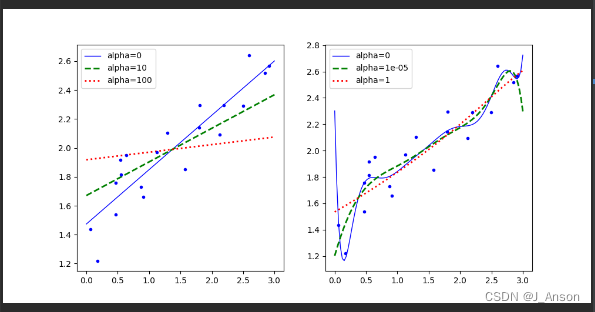
可以看出alpha越小,浮动范围越大,预测结果越不好,拟合效果越不平稳。因此,正则化可以优化拟合参数并减少估计方差。值越大则正则化效果越强。